Écrire des mathématiques
Concevoir le préambule
Rappelez-vous que l’objectif premier de LaTeX est de pouvoir écrire des mathématiques avec une composition irréprochable.
Pour cela, il faut commencer par bien concevoir son préambule, même si LaTeX peut les écrire nativement. C’est dans le préambule que vous devez déclarer tous les packages nécessaires pour parfaitement mener à bien cette tâche.
Pour bien écrire des mathématiques, il vous faudra forcément toute une série de symboles pour rédiger vos formules. C’est le package amssymb qui s’en occupe. Le package mathtools chargera tous les outils nécessaires à vos écrits et chargera aussi l’indispensable package amsmath.
En ce qui concerne la police de caractères, il est souhaitable d’utiliser la famille Fourier, qui est spécialement dessinée pour avoir la meilleure qualité visuelle des symboles mathématiques.
Donc voici un exemple d’un préambule dédié aux écrits mathématiques :
\documentclass[11pt,a4paper]{book}
\usepackage[utf8]{inputenc}
\usepackage[french]{babel}
\usepackage[T1]{fontenc}
\usepackage{mathtools} % Outils mathématiques + amsmath
\usepackage{amssymb} % Symboles mathématiques ...Connaître les modes d’écriture mathématiques
Vous le savez, LaTeX peut écrire nativement des mathématiques. Mais il peut concevoir et afficher des formules mathématiques de plusieurs manières différentes : dans une ligne d’un paragraphe, dans un bloc dédié ou avec un environnement aux lignes numérotées.
1. Le mode d’écriture en ligne
Le premier mode permet d’écrire une formule mathématique dans une ligne d’un paragraphe. Pour cela, vous pouvez utiliser cette syntaxe : $x=2y-z$. La formule est placée entre deux caractères $. Cette syntaxe est celle de la notation « pure » TeX. C’est celle que les puristes LaTeX n’utiliseront pas, car il peut y avoir de rares problèmes de composition, dans la gestion des espaces notamment.
Pour éviter ces rares cas, utilisez plutôt la syntaxe LaTeX : \(x=2y-z\). La formule est placée entre le délimiteur d’ouverture \( et le délimiteur de fermeture \). Cette syntaxe est un peu plus longue à saisir et un peu moins lisible. C’est pour cela que la plupart des rédacteurs utilisent la syntaxe entre les caractères $, malgré les très rares problèmes de composition précédemment évoqués.
Ces deux syntaxes font en fin de compte appel à l’environnement \begin{math}. Ce qui vous permet d’avoir une troisième syntaxe : \begin{math}x=2y-z\end{math}.
Dans tous les cas, ces trois syntaxes afficheront le même rendu. Voici les exemples :
Cras mattis consectetur \(x=2y-z\) purus sit amet fermentum.
Etiam porta sem malesuada magna mollis euismod. Integer
posuere : $x=2y-z$ erat a ante venenatis dapibus posuere
velit aliquet. Lorem ipsum dolor sit amet :
\begin{math}x=2y-z\end{math} consectetur adipiscing elit. Voici l’affichage obtenu :

Vous pouvez tout de suite remarquer que les variables, x, y et z dans cet exemple, sont affichées en italique. C’est l’affichage normalisé de LaTeX.
2. Le mode d’écriture en bloc
Le deuxième mode vous permet d’afficher une formule dans un bloc dédié, en dehors de tout paragraphe de contenu textuel. Pour cela...
Personnaliser la mise en forme
1. La position de la numérotation
Avec l’environnement equation, vous avez vu que les numéros des équations apparaissent sur la droite des pages. C’est le paramètre par défaut. Si vous souhaitez qu’ils apparaissent sur la gauche, paramétrez-le dans le préambule, comme option de la classe de document.
L’option leqno permet d’afficher les numéros à gauche :
\documentclass[11pt,a4paper,leqno]{book} Voici l’affichage obtenu :
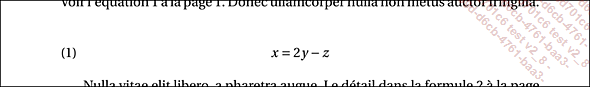
L’option fleqn permet d’avoir la formule alignée à gauche, avec un retrait de première ligne et la numérotation à droite :
\documentclass[11pt,a4paper,fleqn]{book} Voici l’affichage obtenu :

Enfin, vous pouvez avoir une numérotation à gauche et un retrait de première ligne, en indiquant les deux options :
\documentclass[11pt,a4paper,leqno,fleqn]{book} Voici l’affichage obtenu :

La rédaction d’équations mathématiques peut être divisée en plusieurs parties, qui doivent être numérotées en conséquence. L’environnement \begin{subequations} permet de créer une partie logique dans laquelle la numérotation s’incrémente par des lettres alphabétiques en minuscules.
Voici un exemple :
..auctor fringilla.
\begin{equation}
x=2y-z
\end{equation}
Nulla vitae elit libero...
\begin{subequations}
\begin{equation}
2x=3y-4
\end{equation}
Duis mollis, est non commodo...
\begin{equation}
3x=5y+2
\end{equation}
\end{subequations}
Fusce dapibus, tellus ac cursus commodo...
\begin{equation}
x=y-1
\end{equation}
Integer posuere erat... Notez que vous pouvez indenter...
Exploiter les polices de caractères
1. Les familles de caractères
Le mode mathématique permet d’appliquer les différentes familles de caractères de la police choisies. Dans les exemples de ce chapitre, nous utilisons la police Fourier et celle-ci possède les déclinaisons en romain, en télétype et en sans sérif. Maintenant, c’est à vous de décider s’il est opportun de les utiliser dans vos documents.
Pour appliquer ces changements, utilisez les commandes \mathrm{•} (rm pour romain), \mathtt{•} (tt pour télétype) et \mathsf{•} (sf pour sans sérif), dans le mode mathématique.
Voici un exemple, avec respectivement la fonte par défaut, en romain, en télétype et sans sérif :
Duis mollis, est non commodo luctus : $f(x)=2x-4$ nisi erat
porttitor ligula, eget lacinia odio sem nec elit.
Duis mollis, est non commodo luctus : $\mathrm{f(x)=2x-4}$
nisi erat porttitor ligula, eget lacinia odio sem nec elit.
Duis mollis, est non commodo luctus : $\mathtt{f(x)=2x-4}$
nisi erat porttitor ligula, eget lacinia odio sem nec elit.
Duis mollis, est non commodo luctus : $\mathsf{f(x)=2x-4}$
nisi erat porttitor ligula, eget lacinia odio sem nec elit. Voici l’affichage obtenu :

2. Les styles...
Insérer les symboles usuels
1. Les opérateurs usuels
Dans toutes vos équations, vous aurez certainement besoin d’utiliser les opérateurs simples que sont l’addition, la soustraction, la division et la multiplication. Pour les trois premiers opérateurs, il n’y a aucun souci d’affichage, le mode mathématique de LaTeX va parfaitement respecter les usages mathématiques, à savoir que les opérateurs (et les constantes) ne sont pas affichés en italique, contrairement aux variables. Donc vous pouvez utiliser les touches correspondantes sur votre clavier.
Par contre, pour la multiplication, le problème est qu’il ne faut pas confondre la variable x, qui doit être affichée en italique, avec l’opérateur x, qui ne doit pas être en italique. Il faut donc impérativement utiliser la commande \times pour l’opérateur de multiplication.
Voici des exemples :
Duis mollis, est non commodo luctus : $f(x)=2x+4y$ nisi erat
porttitor ligula, eget lacinia odio sem nec elit.
Duis mollis, est non commodo luctus : $f(x)=2x-4y$ nisi erat
porttitor ligula, eget lacinia odio sem nec elit.
Duis mollis, est non commodo luctus : $f(x)=2x/4y$ nisi erat
porttitor ligula, eget lacinia odio sem nec elit.
Duis mollis, est non commodo luctus : $f(x)=2x\times4y$ nisi
erat porttitor ligula, eget lacinia...Utiliser des symboles pour les mathématiques
1. Une liste des symboles
En mathématiques, vous devrez utiliser une multitude de symboles divers et variés. Pour connaître les centaines de symboles à votre disposition, consultez le document The Comprehensive LATEX Symbol List à cette URL : http://ctan.math.utah.edu/ctan/tex-archive/info/symbols/comprehensive/symbols-letter.pdf
Dans ce document de 370 pages, vous trouverez une liste quasi-complète de tous les symboles mathématiques disponibles.
2. Des lettres grecques
Voici quelques lettres grecques à insérer dans vos formules mathématiques :
Alpha : $\alpha$. Beta : $\beta$. Omega : $\omega$ et $\Omega$.
Pi : $\pi$ et $\Pi$. Phi : $\phi $ et $\Phi$. Voici l’affichage obtenu :
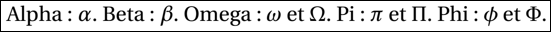
3. Des symboles mathématiques
Voici quelques symboles mathématiques :
D'autres symboles : $\in$ , $\not\in$ , $\exists$ , $\div$ ,
$\approx$ , $\pm$ , $\to$ , $\Rightarrow$ , $\Leftarrow$ ,
$\infty$. Voici l’affichage obtenu :
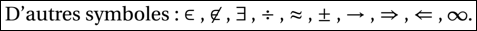
4. Les fonctions trigonométriques
Si vous avez besoin d’insérer les fonctions trigonométriques sinus, cosinus et tangente, vous devez bien respecter cette syntaxe : $\sin~2x$. Il faut utiliser les commandes \sin, \cos et \tan, immédiatement suivies par une espace insécable ~ et par le terme de la fonction.
Voici des exemples, avec, dans la première ligne des syntaxes...
Écrire des dérivées
Pour écrire une dérivée de f(x), utilisez la commande f^\prime(x) ou ^f’(x) avec l’apostrophe simple.
Voici ces deux exemples :
Maecenas sed diam eget risus : $f^\prime(x)=2x-2$ varius
blandit sit amet.
Maecenas sed diam eget risus : $f'(x)=2x-2$ varius blandit
sit amet. Voici l’affichage obtenu :
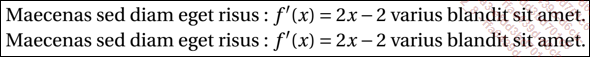
Pour les dérivées secondes, doublez la commande ou les apostrophes. Attention, n’utilisez pas une apostrophe double : ".
Écrire des valeurs absolues
Les valeurs absolues s’obtiennent avec le caractère |. Avec un clavier de PC, utilisez les touches [AltGr]+6, avec le clavier des Mac, utilisez les touches [Alt]+[Shift]+L.
Vous pouvez aussi utiliser la commande \vert pour une seule barre verticale, et \Vert pour une double barre verticale.
Voici deux exemples :
Lorem ipsum : $\vert4x^2-y\vert$ et $\Vert4x^2-y\Vert$ dolor est. Voici l’affichage obtenu :
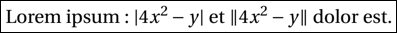
Écrire des fractions
La commande pour écrire des fractions est : \frac{Numérateur}{Dénominateur}.
Voici un exemple simple :
\begin{displaymath}
\frac{2x+3}{4y-2}
\end{displaymath} Voici l’affichage obtenu :
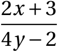
Vous pouvez bien sûr complexifier l’équation en ajoutant d’autres fractions dans le numérateur ou dans le dénominateur. Il faut évidemment faire attention à l’équilibre des accolades : vous devez avoir autant d’accolades ouvrantes, {, que d’accolades fermantes, }.
Voici un exemple plus complexe :
\begin{displaymath}
\frac{(2x+3)(4y-2)}{(2x^2-y)}=\frac{\frac{3x+6}{4y}}{(2x-3y)^2}
\end{displaymath} Voici l’affichage obtenu :
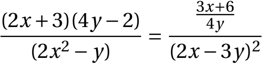
À l’inverse, si vous avez une simple fraction avec un seul numérateur et un seul dénominateur, vous pouvez utiliser la syntaxe : \frac 23. Voici un exemple :
Maecenas sed diam eget risus : $\frac 23$ varius blandit sit
amet non magna. Voici l’affichage obtenu :
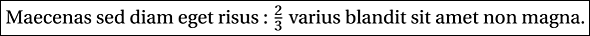
Lorsque vous insérez des fractions dans une ligne d’un paragraphe, LaTeX adapte leur taille au contexte. Dans une ligne, les fractions sont écrites plus petites.
Voici un exemple simple :
Maecenas...Écrire des racines énièmes
Les racines énièmes s’obtiennent avec la commande \sqrt[radical]{Argument}. Si le radical est omis, c’est par défaut une racine carrée.
Voici un exemple simple :
\begin{displaymath}
\sqrt{2x-5}
\end{displaymath} Voici l’affichage obtenu :
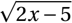
Voici un autre exemple, avec un radical :
\begin{displaymath}
\sqrt[3]{2x-5}
\end{displaymath} Voici l’affichage obtenu :
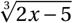
Voici un exemple plus complexe avec des racines imbriquées et une fraction :
\begin{displaymath}
\sqrt[n]{\frac{1}{2x-\sqrt{n^2-3}}}
\end{displaymath} Voici l’affichage obtenu :
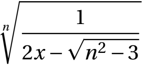
Écrire des sommes et des produits
Pour obtenir une somme, utilisez la commande \sum_{•}^{•}, et pour les produits, utilisez la commande \prod _{•}^{•}.
Voici un exemple d’une somme :
\begin{displaymath}
\sum_{i=n}^{i=1} 2i-1
\end{displaymath} Voici l’affichage obtenu :
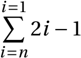
Voici un exemple d’un produit :
\begin{displaymath}
\prod_{i=n}^{i=1} 2i-1
\end{displaymath} Voici l’affichage obtenu :
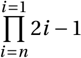
Les deux exemples précédents étaient saisis dans l’environnement \begin{displaymath}. Si vous insérez ces mêmes équations en ligne, l’affichage sera adapté à cet environnement.
Voici ces mêmes équations, mais en ligne, dans des paragraphes :
Lorem Nullam Cras Ridiculus Commodo. Nullam id dolor id nibh
ultricies vehicula : $\sum_{i=n}^{i=1} 2i-1$ dolor. Maecenas
sed diam eget risus varius blandit sit amet non magna.
Aenean eu leo quam.
Lorem Nullam Cras Ridiculus Commodo. Nullam id dolor id nibh
ultricies vehicula : $\prod_{i=n}^{i=1} 2i-1$ dolor.
Maecenas sed diam eget risus varius blandit sit amet non
magna. Aenean eu leo quam. Voici l’affichage obtenu :

Écrire des intégrales
Pour afficher une intégrale, utilisez \int _{•}^{•}. À nouveau, LaTeX adapte l’affichage selon le contexte. Voici deux exemples :
Lorem Nullam Cras Ridiculus Commodo. Nullam id dolor id nibh
ultricies vehicula : $\int_{1}^{n-1}2t-u$ dolor. Maecenas
sed diam eget risus varius blandit sit amet non magna.
Aenean eu leo quam.
\begin{displaymath}
\int_{1}^{n-1}2t-u
\end{displaymath} Voici l’affichage obtenu :

Écrire des limites
Les limites s’obtiennent avec la commande \lim{•}. Voici deux exemples, dans les deux modes mathématiques :
Lorem Nullam Cras Ridiculus Commodo. Nullam id dolor id nibh
ultricies vehicula : $\lim_{n\to\infty}u_n-1$ dolor.
Maecenas sed diam eget risus varius blandit sit amet non
magna. Aenean eu leo quam.
\begin{displaymath}
\lim_{n\to\infty}u_n-1
\end{displaymath} Voici l’affichage obtenu :

Écrire des matrices
Vous pouvez écrire des matrices avec des parenthèses (\begin{pmatrix}), des crochets (\begin{bmatrix}), des barres verticales (\begin{vmatrix}), des accolades (\begin{Bmatrix}) ou sans délimiteurs (\begin{matrix}).
Attention les matrices ne peuvent s’utiliser qu’avec le package amsmath, qui est chargé par le package mathtools.
Voici la syntaxe utilisée pour les matrices avec des parenthèses :
\begin{displaymath}
\begin{pmatrix}
a&b \\ c&d
\end{pmatrix}
\end{displaymath} Voici l’affichage obtenu avec toutes les possibilités indiquées précédemment :
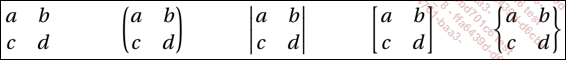
Chaque terme de la matrice est séparé par une esperluette, &, et le passage à la ligne se fait avec un double contre-oblique : \\.
\begin{displaymath}
\begin{pmatrix}
a&b&c&d \\
e&f&g&h \\
i&j&k&l
\end{pmatrix}
\end{displaymath} Voici l’affichage obtenu :
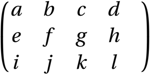
Écrire des vecteurs, des arcs et un trait suscrit
Les vecteurs s’obtiennent avec la commande \overrightarrow{•} et les arcs avec \widehat{•}.
Voici des exemples :
Lorem ipsum : $3\overrightarrow{AB}+2\overrightarrow{CD}$.
Cras mattis : $\widehat{AB}+\widehat{C\ldots F}$. Voici l’affichage obtenu :
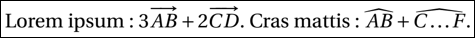
Vous pouvez bien sûr afficher un vecteur sur une seule lettre avec la commande \vec{•}.
Voici un exemple simple :
Donec sed odio dui $\vec{u}$ risus varius blandit Voici l’affichage obtenu :
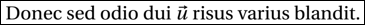
Attention, pour les lettre i et j, il ne faut pas afficher leur point. Il faut donc utiliser les commandes \imath et \jmath.
Voici, avec les deux premiers exemples, les syntaxes à ne pas utiliser, et les bonnes syntaxes dans les deux derniers exemples :
Cras mattis $\vec{i}$ consectetur $\vec{j}$ purus sit
$\vec{\imath}$ amet $\vec{\jmath}$ fermentum. Voici l’affichage obtenu :
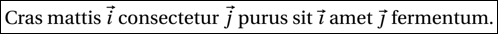
Pour afficher un trait suscrit, utilisez la commande \overline{•}.
Voici un exemple :
Lorem ipsum : $\overline{ABC}$ dolor est. Voici l’affichage obtenu :
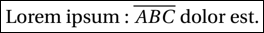
Regrouper des éléments et superposer des symboles
Il est assez courant d’avoir besoin de regrouper des éléments dans une formule. Le mode mathématique de LaTeX nous permet d’utiliser des accolades ou des crochets au-dessus ou en dessous des termes à regrouper.
Pour afficher une accolade au-dessus de certains éléments de la formule, utilisez cette syntaxe : \overbrace{Eléments à regrouper}^{Eléments au-dessus}. Détaillons cette commande.
-
\overbrace affiche l’accolade horizontale au-dessus des éléments à regrouper.
-
{Eléments à regrouper} indique les éléments de l’équation à placer sous l’accolade.
-
^ permet d’indiquer les éléments à afficher au-dessus de l’accolade. Cela reprend le principe de l’exposant.
-
{Eléments au-dessus} indique les éléments de l’équation à placer au-dessus de l’accolade.
Vous obtiendrez le même principe avec \underbrace, accolade au-dessous, et _ (syntaxe de l’indice). Pour les crochets, utilisez \overbracket et \underbracket.
Voici des exemples :
\begin{displaymath}
\overbrace{a_1+a_2+\ldots +a_n}^{n~\text{termes}}
\end{displaymath}
... ...Mettre en forme et mettre en page les mathématiques
1. Les coupures dans les équations
Lorsque vous écrivez des équations dans une ligne d’un paragraphe, il se peut qu’elles soient coupées en fin de ligne. Cela nuit à la visibilité, à la lisibilité et à la compréhension des équations.
Voici un exemple :
Lorem Nullam Cras Ridiculus Commodo. Nullam id dolor id :
$f(x)=2x^2-3x+4$ dolor. Maecenas sed diam eget risus varius
blandit sit amet non magna. Aenean eu leo quam. Voici l’affichage obtenu :

Pour éviter cela, vous pouvez utiliser la commande \mbox{•}, qui crée une boîte dont le contenu ne sera pas coupé en fin de ligne. Mais l’inconvénient, c’est que cela provoque un « débordement » de la boîte dans la marge droite du paragraphe. Il faut donc que l’équation ne soit pas trop longue. Sinon, placez-la dans un environnement \begin{displaymath}.
Voici la syntaxe à utiliser :
Lorem Nullam Cras Ridiculus Commodo. Nullam id dolor id :
\mbox{$f(x)=2x^2-3x+4$} dolor. Maecenas sed diam eget risus
varius blandit sit amet non magna. Aenean eu leo quam. Voici l’affichage obtenu :

2. Les équations fantômes
Il se peut que vous souhaitiez proposer de résoudre des équations simples dans une ligne de paragraphe...
Créer des devoirs et des examens
1. La classe de document exam
Tout enseignant en mathématiques devra un jour créer des devoirs et des examens. Pour l’aider dans cette tâche, l’enseignant pourra utiliser la classe de document exam : https://www.ctan.org/pkg/exam. Cette classe propose des solutions très pratiques pour obtenir des énoncés numérotés, des solutions aux exercices et un système de notation.
Nous n’allons pas apprendre de manière exhaustive toutes les fonctionnalités de cette classe, nous allons nous concentrer sur l’essentiel.
L’installation de cette classe se fait, comme toujours, à la première ligne du préambule :
\documentclass[11pt,a4paper]{exam} Dans cet exemple, nous indiquons une taille de caractères de 11 points et du papier A4. Bien sûr, vous faites ce que vous voulez.
Voici le préambule complet de notre exemple :
\documentclass[11pt,a4paper]{exam}
\usepackage[utf8]{inputenc}
\usepackage[french]{babel}
\usepackage[T1]{fontenc}
\usepackage{mathtools} % Outils mathématiques + amsmath
\usepackage{amssymb} % Symboles mathématiques
\usepackage{fourier} % Fonte pour les mathématiques 2. La structure du document
La classe de document permet de structurer le document à l’aide de groupes de questions. Vous pouvez avoir plusieurs groupes de questions dans le cas d’un devoir ou d’un examen conséquent. Dans chaque groupe de questions vous insérez toutes les questions voulues. De plus, pour chaque question vous pouvez ajouter la solution, qui pourra être masquée et affichée selon les besoins.
Donc voici la structure d’un groupe de questions :
\begin{questions}
\question ...
\begin{solution}
...
\end{solution}
\question ...
\begin{solution}
...
\end{solution}
\question ...
\begin{solution}
... ...Utiliser Texmaker pour les mathématiques
Texmaker est particulièrement bien adapté à la composition des mathématiques. Il nous offre de très nombreuses facilités.
Tout d’abord, dans l’assistant de nouveau document, dans le menu Assistants - Assistant nouveau document, vous avez accès aux packages AMS et Fourier.
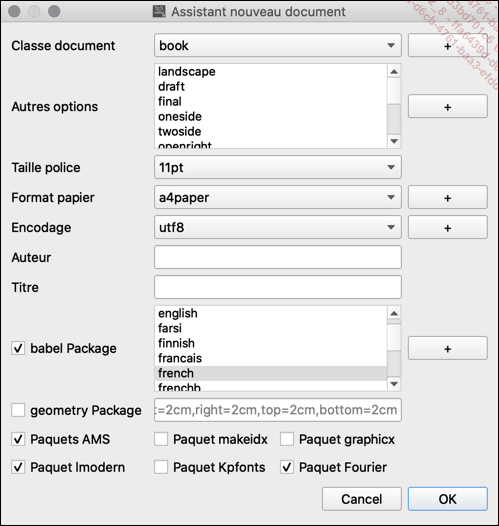
Ensuite, dans le menu Math, vous avez à votre disposition la plupart des commandes usuelles pour écrire des mathématiques.
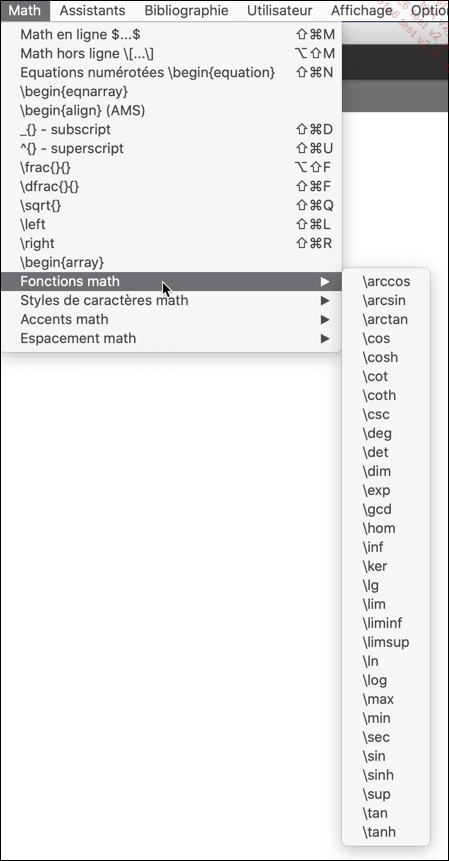
Pour accéder aux symboles et opérateurs usuels, utilisez la deuxième colonne d’outils :

Vous pourrez insérer : les délimiteurs d’une équation en ligne, $ $, un indice, _{•}, un exposant, ^{•}, une fraction, \frac{•}{•}, une fraction plus grande, \dfrac{•}{•}, et une racine carrée, \sqrt{•}.
Dans la première colonne d’outils à gauche, vous avez accès à de très nombreux symboles, rangés par catégorie.
Vous avez les Symboles et opérateurs :
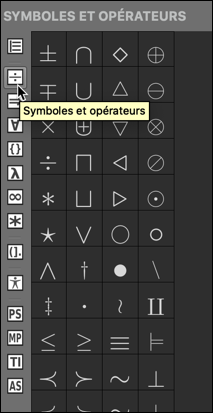
Les Flèches :
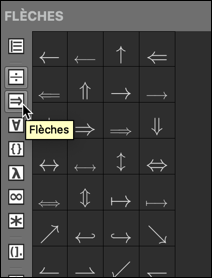
Divers symboles :
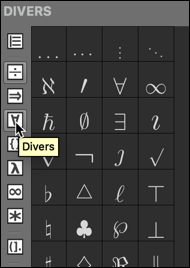
Puis, les Délimiteurs, les Lettres grecques, les Symboles fréquents et les left/right.
La catégorie Symboles favoris permet de mémoriser les symboles que vous utilisez le plus. Pour mémoriser un symbole, faites un clic...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
