Présentation de la notion d’algorithme

Un algorithme est la description des opérations nécessaires pour obtenir un résultat à partir de valeurs d’entrée, les « données ». Un programme est un algorithme écrit dans un langage spécifique, nous y reviendrons plus tard.

Une recette de cuisine peut être considérée comme un algorithme. À titre d’exemple, la fabrication d’un gâteau est basée sur des ingrédients (lait, beurre, farine, sucre...) et une démarche méthodique (recette de la grand-mère) sera appliquée pour mettre en œuvre ces ingrédients (mélange, temps de cuisson...). Vous l’aurez compris dans notre vie de tous les jours nous utilisons des algorithmes sans réellement nous en rendre compte (recettes, notices, plans de conception, modèles...).

Reconsidérons notre exemple de la recette de cuisine. En son absence, il est possible de réussir son plat par une succession de tentatives (dosages divers, temps de cuisson approximatifs). Évidemment cette démarche (même si certains y trouveront du plaisir) est assez inefficace (perte de temps et gâchis des ingrédients).

La programmation va être le moyen de définir et de spécifier à l’ordinateur l’ensemble des opérations...

Notion de variable

1. Présentation des notions de variable et de type

Un algorithme manipule des objets sur lesquels il peut effectuer des actions. Les objets simples sont :

des nombres (3.14159, 1980, 9...),
des caractères ("A", "9"...) et des chaînes de caractères ("PAULINA"...),
des valeurs booléennes ou logiques (vrai ou faux).

Pour pouvoir manipuler ces objets, des opérations sont disponibles. Ces objets ainsi que les opérations qui leur sont associées doivent être parfaitement définis. Analysons les trois exemples suivants qui sont des situations d’échange entre un client et un vendeur.

Exemple 1 :

"Bonjour Monsieur l’épicier, je voudrais 1 kg et 1 kg."
"??"

Exemple 2 :

"Bonjour Monsieur l’épicier, je voudrais 1 kg de riz et 1 kg de vin."
"Voici votre kilo de riz et que voulez-vous par ailleurs ?"

Exemple 3 :

"Bonjour Monsieur l’épicier, je voudrais 1 kg de riz et 1 litre de vin."
"Voilà je vous ai tout rangé dans un petit sac"

On constate sur ces exemples la nécessité :

de citer la nature des objets que l’on veut manipuler (riz, vin...),
de ne pas utiliser ces objets n’importe comment (on pèse du riz, on boit du vin...), c’est-à-dire qu’à chaque nature d’objet sont liées des opérations particulières.

On appelle type l’association :

d’une nature d’objets (riz, vin, ou encore entiers, réels...),
et des opérations associées (peser, laver, cuire le riz, additionner, multiplier des entiers...).

2. Types de base et opérations associées

On distingue quatre types de base : entier, réel, booléen, caractère.

Le type entier :

Les valeurs sont des nombres entiers.
Notation : la notation décimale est utilisée (Exemples : 365, -15).
Opérations : addition, soustraction, multiplication, division entière, modulo (reste de la division entière)...

Le type réel :

Les valeurs sont des nombres réels.
Notation : le point anglo-saxon remplace la virgule (Ex : 124.89, 0.136, 1986).
Opérations : celles utilisées usuellement sur les réels en arithmétique.

Le type booléen :

Il n’existe que deux valeurs booléennes signifiant vrai ou faux.
Notation : Vrai, Faux.
Opérations : on utilise les opérateurs logiques usuels (Non, Ou, Et).

Rappelons le fonctionnement des opérateurs logiques Non, Et et Ou au travers de tableaux de synthèse :

A	Non A
Vrai	Faux
Faux	Vrai

A	B	A Ou B
Vrai	Faux	Vrai
Faux	Vrai	Vrai
Faux	Faux	Faux
Vrai	Vrai	Vrai

A	B	A Et B
Vrai	Faux	Faux
Faux	Vrai	Faux
Faux	Faux	Faux
Vrai	Vrai	Vrai

En résumé :

Le contraire de Faux est Vrai et inversement (cf. tableau du Non).
Avec le Ou logique, il suffit que l’un des opérandes (A, B) soit Vrai pour que le résultat A Ou B soit Vrai (cf. tableau du Ou).
Avec le Et logique, il faut que les deux opérandes (A, B) soient simultanément Vrai pour que le résultat A Et B soit Vrai (cf. tableau du Et).

3. Intérêt...

Manipulation des variables

1. Nommage des variables

Lors de l’analyse d’un problème, on est souvent amené à le décomposer en sous-problèmes qui doivent être résolus dans un ordre séquentiel bien précis. Chaque sous-problème produit des résultats qui peuvent être utilisés dans les sous-problèmes qui suivent. Il convient donc, pour pouvoir manipuler ces résultats, de les nommer. Ce nommage se fait par l’intermédiaire d’un identificateur. On parle aussi très souvent de variable mémoire.

À chaque variable mémoire, on associe les caractéristiques suivantes :

sa dénomination, qui doit être judicieuse (deux résultats différents sont désignés par un identificateur différent),
son type (ensemble auquel appartient la valeur qu’il désigne).

Ces caractéristiques sont précisées lors de la déclaration de la variable mémoire.

Syntaxe de la déclaration :

Type IDENTIFICATEUR

Type est le type et IDENTIFICATEUR la dénomination de la variable mémoire.

Exemples :

Réel PI

Car SEPARATEUR

Bool TEST

Ent NBMOIS, NBJOURS

Une fois une variable mémoire définie, on ne peut plus changer son type.

Toute variable mémoire utilisée dans un algorithme doit avoir été déclarée auparavant.

Dans la suite de ce support de cours, il a été choisi de nommer les variables mémoire en majuscules pour une meilleure lisibilité. Sachez que de nombreux langages de programmation sont sensibles à la "casse" des variables mémoire (une variable MONTANT est différente d’une variable Montant !!!).

Évidemment en programmation ensuite (JavaScript dans notre cas), des conventions de nommages différentes pourront vous être proposées.

En JavaScript pour les variables mémoire (et les fonctions) la convention communément acceptée est le "camelCaps", c’est-à-dire que les noms doivent commencer systématiquement par une minuscule et ensuite des majuscules viendront s’insérer en début de chaque mot constituant le nom de la variable. Par exemple une variable comme CUMUL_ANNUEL (la convention dans cette présentation de l’algorithmique) sera codée cumulAnnuel en JavaScript.

Vous pourrez noter dans la suite du livre que dans de nombreux scripts JavaScript proposés la convention camelCaps n’est pas utilisée. Le choix ayant été fait de ne pas modifier les noms des variables mémoire des algorithmes sous-jacents.

2. Affectation

L’affectation consiste à stocker ou encore à imputer une expression à une variable mémoire. La syntaxe retenue dans cette présentation de l’algorithmique est :

IDENTIFICATEUR <- expression

L’affectation est notée par le symbole "<-" (et non pas le "=" qui sert à faire des comparaisons d’égalité).

L’expression doit être du type des valeurs désignées par l’identificateur. Cette expression devient la nouvelle valeur désignée...

Fonctions prédéfinies

Une fonction prédéfinie est un "microprogramme" autonome auquel il est possible de demander un traitement (un calcul en général) par passage d’un ou de plusieurs paramètres. Une fois le calcul assuré, la fonction restitue une valeur de retour (la réponse) au demandeur (séquence de code ayant fait appel à la fonction). Cette notion vous est sûrement familière car vous avez par exemple utilisé des fonctions natives sous Microsoft Excel (SOMME, RECHERCHEV...).

Nous verrons plus tard dans cette présentation de l’algorithmique (et aussi surtout sous JavaScript) comment développer ses propres fonctions.

L’objectif n’est pas ici d’énumérer la liste des fonctions courantes en algorithmique (elle peut d’ailleurs varier d’un auteur à un autre) mais plutôt de vous montrer comment elles peuvent s’utiliser. Une présentation au travers d’exemples ou d’exercices va être privilégiée.

1. Exercice n°4 : Affichage de la longueur d’un nom

Sujet

Écrire un algorithme permettant la saisie au clavier d’un nom pour afficher le nombre de caractères.

Complément de cours : Une fonction Longueur(variable_chaîne) prédéfinie sera utilisée pour déterminer le nombre de caractères du mot saisi.

Corrigés

Début
	Co Déclarations Fco Car NOM
	Co Saisie du nom au clavier Fco Ecrire("Nom : ") NOM <- Lire
	Co Affichage du résultat Fco Ecrire(NOM, " contient " , Longueur(NOM), " caractère(s)")
Fin

ou encore :

Début
	Co Déclarations Fco Car NOM Ent NB_CAR
	Co Saisie du nom au clavier Fco Ecrire("Nom : ") NOM <- Lire
	Co Affichage du résultat Fco NB_CAR <- Longueur(NOM) Ecrire(NOM, " contient " , NB_CAR, " caractère(s)")
Fin

2. Exercice n°5 : Détermination des initiales

Sujet

Écrire un algorithme qui permettra l’extraction des initiales d’une personne dont le prénom et le nom seront saisis au clavier (exemple CV pour Christian VIGOUROUX).

Complément de cours : une fonction Sous_chaîne(CHAINE, POSITION_DEBUT, [POSITION_FIN]) prédéfinie sera utilisée.

Un paramètre...

Traitements conditionnés

Dans beaucoup de situations, des actions ne sont à effectuer que si certaines conditions sont remplies :

Une équation du second degré a 0, 1 ou 2 solutions réelles suivant que le discriminant soit négatif, nul ou positif.
Si une quantité d’articles en stock tombe en dessous d’un certain seuil, il faut émettre une commande.
S’il fait beau alors on va à la plage, sinon on fait de l’algorithmique ensemble.
S’il ne fait pas beau alors on fait de l’algorithmique ensemble.

Chacun de ces choix est conditionné par une expression booléenne qui, lorsqu’elle est vraie, entraîne l’exécution du traitement associé.

La syntaxe algorithmique pour programmer des traitements conditionnés est des plus simples :

Si Condition
Alors
	T1
[Sinon
	T2]
Finsi

Juste quelques remarques sur cette structure très intuitive :

Condition est une expression à résultat booléen (Vrai ou Faux).
T1 et T2 sont des traitements.
Finsi signifie la fin du si.
Une forme simplifiée, sans l’alternative, existe (sans Sinon T2).
Le test sur la condition se fait sur une hypothèse de condition vraie.
Le tracé d’un trait vertical (à gauche) entre Si et Finsi sera un moyen mnémotechnique pour ne pas oublier le Finsi.
Pensez à indenter les traitements T1 et T2.

L’ordinogramme correspondant à cette structure est le suivant :

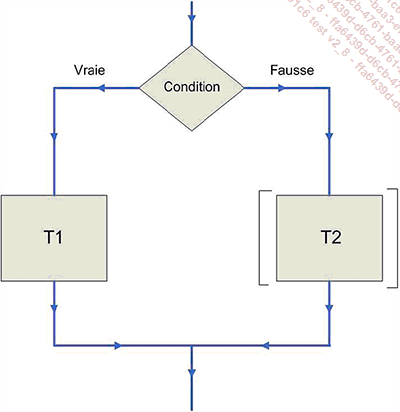
Dans l’exemple présenté ci-après, une variable de nom NBLU est affectée d’une valeur saisie au clavier et l’algorithme précise ensuite s’il s’agit d’une valeur paire ou impaire :

Début
	Co Déclarations Fco Ent NBLU
	Co Saisie clavier Fco Ecrire("Nombre : ")
	NBLU <- Lire
	Co Détermination de la parité Fco Si NBLU Mod 2 = 0
	Alors
		Ecrire(NBLU, " est pair")
	Sinon
		Ecrire(NBLU, " est impair")
	Finsi
Fin

1. Exercice n°6 : Polynôme du second degré

Sujet

Calculer les racines d’un polynôme du second degré Ax²+Bx+C (avec A<>0 dans l’absolu mais ce test ne sera pas effectué ici). Les valeurs A, B et C seront saisies au clavier.

Corrigé

Début
		Co Déclarations Fco Réel A, B, C, DELTA
		Co Saisie des paramètres Fco Ecrire("A : ") A <- Lire
		Ecrire("B : ") B <- Lire
		Ecrire("C : ") C <- Lire
		Co Calcul du discriminant Fco DELTA <- (B * B) - (4 * A * C)
		Co Détermination du nombre de racines Fco Si DELTA < 0
		Alors
			Ecrire("Pas de solutions")
		Sinon
			Si DELTA = 0 Alors Ecrire("Solution unique = ", -B / (2 * A))
		Sinon
			Ecrire("Deux racines : ", (-B+DELTA*0.5)/(2A), " et ", (-B-DELTA*0.5)/(2A))
		Finsi
	Finsi
Fin

L’intérêt de cet exercice, outre celui de vous faire réviser un peu les mathématiques, est de montrer qu’il...

Structures itératives

1. Principe des itérations

Dans la plupart des problèmes, certaines actions doivent être exécutées plusieurs fois.

Quand le nombre de répétitions est grand, il est fastidieux de réécrire n fois la même séquence de code. Cette réécriture est même impossible dans le cas où le nombre de répétitions (itérations) est inconnu a priori (traiter un ensemble de données jusqu’à ce qu’il n’y en ait plus).

Il faut pouvoir exprimer la répétition d’une action, qui une fois initialisée se continuera jusqu’à ce qu’un certain événement se produise. Cet événement d’arrêt sera spécifié dans l’algorithme par l’intermédiaire d’une condition.

2. Structures itératives de base

Étudions quatre types d’itérations (boucles) dont vous trouverez l’équivalent dans les principaux langages de programmation.

Boucle "Tant que" avec un test en début d’itération :

Tantque Condition Faire
	Actions
Refaire

Boucle "Jusqu’à" avec un test en début d’itération :

Jqa Condition Faire
	Actions
Refaire

Boucle "Tant que" avec un test en fin d’itération :

Faire
	Actions
Tantque Condition Refaire

Boucle "Jusqu’à" avec un test en fin d’itération :

Faire
	Actions
Jqa Condition Refaire

Ces quatre boucles ont un certain nombre de points communs :

Jqa est une abréviation pour Jusqu’à
Tantque est une abréviation pour Tant que
Condition est une expression booléenne de résultat Vrai ou Faux
Actions représente une séquence d’actions

Avec les deux dernières itérations pour lesquelles le test se fait en fin de boucle, les Actions sont effectuées au moins une fois.

Les boucles "Tant que" et "Jusqu’à" ont un fonctionnement très proche dans la mesure où il suffit d’inverser la condition pour passer d’une syntaxe à l’autre. Par exemple COMPTEUR > 10 dans le cas d’une boucle "Tant que" deviendra COMPTEUR <= 10 dans le cas d’une boucle "Jusqu’à".

L’ordinogramme suivant correspond aux structures "Tant que" et "Jusqu’à" (avec un test en début d’itération) :

Dans le cas d’une boucle Jqa :

la flèche reliant "Condition" à "Actions" correspond à l’état Faux de la Condition,
la flèche reliant "Condition" à "Actions suivantes" correspond à l’état Vrai de la Condition.

Dans le cas d’une boucle Tantque :

la flèche reliant "Condition" à "Actions" correspond à l’état Vrai de la Condition,
la flèche reliant "Condition" à "Actions suivantes" correspond à l’état Faux de la Condition.

3. Exercice n°9 : Moyenne de 10 nombres

Sujet

Calculer et afficher la moyenne...

Tableaux à dimension unique

Un tableau regroupe plusieurs valeurs de même type. On peut nommer globalement toutes les valeurs ou avoir une désignation précise d’une des valeurs par une opération d’indiçage.

Par exemple, considérons ALPHABET comme l’ensemble des lettres de l’alphabet. Dans ce cas :

ALPHABET désigne un tableau qui pourrait servir à stocker l’ensemble des lettres de l’alphabet.
ALPHABET(14) pourrait représenter la lettre "N".
l’entier 14 est appelé indice.

Dans un algorithme, tout comme pour les variables (simples) vues jusqu’à présent, les tableaux doivent être déclarés avant de pouvoir être utilisés. La syntaxe de déclaration est :

Type IDENTIFICATEUR(INF:SUP)

Notons ceci au niveau de cette déclaration :

IDENTIFICATEUR est le nom global du tableau (nom librement choisi par le programmeur, en majuscules si possible).
Type indique le type des éléments du tableau et tous les éléments du tableau ont le même type (Ent, Réel, Car et Bool).
INF et SUP sont respectivement les bornes inférieure et supérieure de l’intervalle de variation de l’indice du tableau. Un tel tableau possède N éléments où N = SUP - INF + 1.
INF et SUP sont des constantes définies à l’avance (pas de dimensionnement "dynamique" bien que certains langages de programmation le permettent).
Dans certains langages de programmation, la valeur INF peut ne pas être exprimée. Dans ce cas la valeur INF est implicitement considérée comme étant un 1 (parfois aussi un 0). Quand...

Tableaux à dimensions multiples

Lorsque les éléments d’un tableau sont eux-mêmes des tableaux, on parle de tableau à plusieurs dimensions.

Au niveau de la déclaration de ce genre de tableau, pas de surprise, il faut annoncer les limites de l’indice pour chacune des dimensions :

Type IDENTIFICATEUR(INF1:SUP1, ..., INFi:SUPi, ..., INFn:SUPn)

Pour accéder aux différentes cellules d’un tableau à plusieurs dimensions, il faut tout naturellement indiquer une valeur d’indice pour chacune d’entre elles. À titre d’exemple pour un tableau à deux dimensions (tableau de lignes subdivisées en colonnes comme une matrice 2D sous Microsoft Excel), le premier indice conventionnellement désigne le numéro de la ligne et le second indice le numéro de la colonne de la cellule à laquelle il est fait référence. La syntaxe est donc :

IDENTIFICATEUR(INDICE1, ..., INDICEi, ..., INDICEn)

1. Exercice n°15 : Mini-tableur

Sujet

Soit le tableau TB à deux dimensions comportant quatre lignes et cinq colonnes. Réaliser les traitements suivants :

saisir au clavier des valeurs dans les trois premières lignes et les quatre premières colonnes (on conserve la dernière ligne et la dernière colonne libres pour des sommations de lignes et de colonnes),
additionner les colonnes...

Procédures, fonctions et passage de paramètres

1. Les objectifs

Ces nouveaux mécanismes permettent au programmeur de traiter un problème sans se soucier, dans un premier temps, du règlement dans le détail des sous-problèmes. Il s’agit d’outils très similaires aux fonctions mathématiques.

En programmation, une procédure ou une fonction représente un algorithme opérant sur des arguments ou paramètres formels (valeurs fictives en quelque sorte). L’exécution de cet algorithme se produit à l’appel de la procédure ou de la fonction. Les données de cet algorithme appelé sont alors les paramètres effectifs (provenant de l’algorithme appelant).

L’intérêt méthodologique de ces mécanismes consiste essentiellement, dans une première étape, à convertir les sous-problèmes en procédures (ou en fonctions) et à traiter le problème général (ou principal) comme si ces sous-problèmes étaient résolus. Dans une seconde étape, ces procédures ou fonctions sont décrites. Un autre intérêt réside dans le fait que si le même sous-problème doit être résolu plusieurs fois avec des paramètres effectifs différents, l’emploi d’une procédure ou d’une fonction permet une meilleure lisibilité de l’algorithme.

2. Les procédures

Débutons l’étude de ce mécanisme par la syntaxe de la déclaration :

Procédure NOM_PROCEDURE([Type1 IDFO1, ..., Typei IDFOi])
	Corps de la procédure
Fin_procédure

Dans cette déclaration :

NOM_PROCEDURE est un nom librement choisi par le programmeur.
IDFOi est le nom du ième paramètre formel de la procédure.
Typei est le type du ième paramètre formel de la procédure.
La procédure ne rend pas de valeurs à moins qu’elle n’intervienne sur des variables de portée (accessibilité) globale.
Procédure et Fin_procédure sont des mots réservés.

L’appel d’une procédure depuis une autre procédure ou depuis l’algorithme principal se fait en respectant le schéma suivant :

NOM_PROCEDURE(IDEF1, IDEFi, ..., IDEFn)

avec :

NOM_PROCEDURE qui est un nom librement choisi par le programmeur,
IDEFi qui est le nom du ième paramètre effectif.

3. Exercice n°16 : Appel d’une procédure avec passage de paramètres

Sujet

Appeler une procédure affichant le double des valeurs effectives passées en paramètres (les deux valeurs passées en paramètres seront à saisir au clavier).

Corrigé

Début
	Co Utilisation d’une procédure affichant le double d’un couple de valeurs Fco
	Co Procédure DOUBLE Fco Procédure DOUBLE(Ent X, Ent Y)
		X <- X * 2 Y <- Y * 2 Ecrire("Le couple doublé est (", X, ",", Y, ")")
	Fin_procédure
	Co Traitement appelant Fco Ent A, B, C, D Ecrire("Programme doublant les valeurs de couples")...