Systèmes experts
Présentation du chapitre
Bien souvent, on aimerait qu’un ordinateur soit capable de nous donner une information que l’on ne connaît pas à partir de faits connus.
Les êtres humains eux-mêmes ne savent pas toujours déduire de nouveaux faits à partir d’autres faits qui leur sont connus et nécessitent l’aide d’un expert. Par exemple dans le cas d’une panne automobile, la majorité des personnes ne peut pas déterminer l’origine de celle-ci et se tourne alors vers le garagiste (l’expert). Celui-ci, grâce à ses connaissances, va pouvoir trouver la panne (et la réparer, normalement).
Beaucoup d’emplois sont constitués de ces experts. Les médecins, les assureurs ou les agents immobiliers n’en sont que quelques exemples.
L’intelligence artificielle peut nous aider, en créant un programme informatique appelé système expert qui jouera le rôle de ce professionnel. Dans certains cas comme la médecine, cet outil pourra devenir une aide au spécialiste lui-même car le domaine étudié est très vaste. Il est en effet rare que l’expert humain puisse être complètement remplacé, et il sera souvent là en appui pour confirmer la conclusion du système, en lui faisant tout de même gagner un temps précieux. Dans d’autres...
Exemple : un système expert en polygones
Cette section permet de voir le fonctionnement détaillé d’un système expert dont le but est de déterminer le nom d’un polygone (par exemple un rectangle) en fonction de caractéristiques sur la forme (le nombre de côtés, les angles droits...). Un petit rappel de géométrie commence donc ce chapitre.
Un polygone est défini comme une forme géométrique possédant au moins trois côtés. L’ordre d’un polygone correspond au nombre de ses côtés.
1. Triangles
Si l’ordre d’un polygone vaut 3, il possède donc trois côtés et il s’agit d’un triangle. Celui-ci peut être quelconque, rectangle, isocèle, rectangle isocèle ou équilatéral.
Les figures suivantes rappellent les particularités de chacun.
 |
Triangle quelconque : possède trois côtés de tailles différentes et aucun angle droit. |
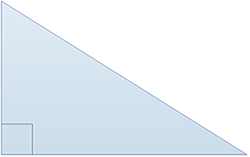 |
Triangle rectangle : possède trois côtés de tailles différentes et un angle droit. |
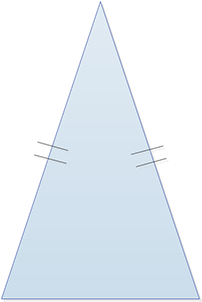 |
Triangle isocèle : possède deux côtés de même taille, mais pas d’angle droit. |
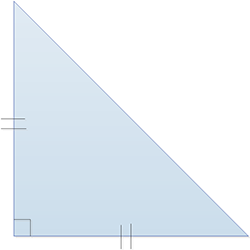 |
Triangle rectangle isocèle : cumule les deux côtés égaux du triangle isocèle et l’angle droit du triangle rectangle. |
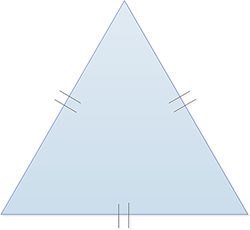 |
Triangle équilatéral... |
Contenu d’un système expert
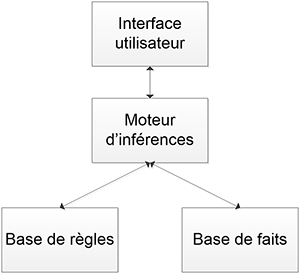
Un système expert est constitué de différentes parties liées entre elles :
-
Une base de règles qui représente les connaissances de l’expert.
-
Une base de faits qui représente les connaissances actuelles du système sur un cas précis.
-
Un moteur d’inférences pour appliquer les règles.
-
Une interface avec l’utilisateur.
Le schéma suivant indique les liens entre ces différentes parties, qui seront détaillées ensuite.
1. Base de règles
Un système expert contient un ensemble de règles nommé base de règles. Celles-ci représentent les connaissances de l’expert sur le domaine.
Ces règles sont toujours de la forme :
SI (ensemble de conditions) ALORS nouvelle connaissance Les conditions d’application d’une règle sont appelées les prémisses. Il peut y avoir plusieurs prémisses, elles sont alors reliées par une coordination ET, signifiant qu’elles doivent toutes être vraies pour que la règle s’applique.
Si la règle nécessite une coordination OU, on la découpera en deux règles distinctes équivalentes. Ainsi, la règle :
Si (A OU B) alors C Deviendra :
Si A alors C
Si B alors C Les nouvelles connaissances sont appelées conclusions.
Pour notre système expert sur les formes géométriques, voici les règles concernant les triangles :
SI (ordre vaut 3) ALORS c'est un triangle SI (triangle ET 1 angle droit) ALORS c'est un triangle rectangle SI (triangle ET 2 côtés de même taille) ALORS c'est un triangle isocèle SI (triangle rectangle ET triangle isocèle) ALORS c'est un triangle
rectangle isocèle SI (triangle ET côtés tous égaux) ALORS c'est un triangle équilatéral Il existerait d’autres règles pour les quadrilatères et les polygones d’ordre supérieur. On voit que très rapidement le nombre de règles peut être important.
De plus, selon le système utilisé, chaque règle doit suivre une syntaxe précise et imposée.
En particulier, les prémisses et conclusions peuvent être demandées sous la forme...
Types d’inférences
Les moteurs d’inférences peuvent enchaîner les règles de différentes façons : c’est ce que l’on appelle le chaînage. Les deux principaux chaînages sont le chaînage avant et le chaînage arrière, mais il existe des moteurs possédant un chaînage mixte.
1. Chaînage avant
a. Principe
Un moteur à chaînage avant est aussi appelé un moteur à inférences dirigé par les données.
Dans ce mode de chaînage, on part des données disponibles en base de faits, et on teste pour chaque règle si elle peut s’appliquer ou non.
Si oui, on l’applique et on rajoute la conclusion à la base de faits.
Le moteur explore donc toutes les possibilités, jusqu’à trouver le fait recherché ou jusqu’à ne plus pouvoir appliquer de nouvelles règles.
Ce mode de chaînage est celui proposé par défaut dans des langages de type CLIPS (C Language Integrated Production System), spécialisés dans la construction de systèmes experts.
b. Application à un exemple
Dans le cas de notre système expert sur les polygones, supposons que nous partions des faits suivants :
-
L’ordre vaut 3.
-
Il y a un angle droit.
-
Deux côtés sont de même taille.
On commence par appliquer la règle suivante, qui ajoute dans la base de faits que la forme est un triangle :
SI (ordre vaut 3) ALORS c'est un triangle On peut ensuite en déduire que c’est un triangle rectangle grâce à la règle suivante :
SI (triangle ET 1 angle droit) ALORS c'est un triangle rectangle De même, on sait que c’est un triangle isocèle :
SI (triangle ET 2 côtés...Étapes de construction d’un système
Pour créer intégralement un système expert, il est important de suivre différentes étapes qui font entrer en jeu des compétences et donc des profils professionnels différents.
Globalement, il y a quatre étapes présentées dans la figure suivante, avec les principaux rôles nécessaires sous chaque étape :
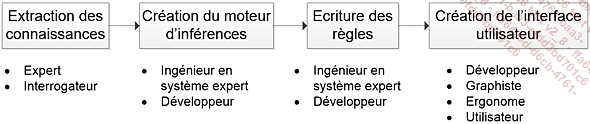
1. Extraction des connaissances
La première étape consiste à extraire les connaissances. Pour cela, il faut trouver un expert qui sera interrogé pour comprendre les règles sous-jacentes aux décisions qu’il prend dans son travail. Cette phase peut paraître simple mais elle est en fait très complexe. En effet, un expert ne réfléchit pas par règles, il a des automatismes qu’il faut arriver à lui faire expliciter.
Prenons l’exemple des insectes. Face à des insectes peu courants ou inconnus, il paraît assez facile de déterminer des règles qui permettent d’arriver au résultat voulu. Mais quelles règles applique-t-on pour reconnaître une mouche d’un moustique, un escargot d’une limace, une fourmi d’un cloporte, ou encore une coccinelle d’un gendarme ?
C’est donc en posant différentes questions à l’expert que l’on pourra l’amener...
Performance et améliorations
Un point n’a jamais été évoqué jusqu’à présent : celui des performances. Celui-ci est pourtant primordial pour la réussite du système. Nous allons donc voir quels sont les critères de performance et comment construire un système permettant de les améliorer.
1. Critères de performance
Les performances d’un système expert, surtout s’il est composé de nombreuses règles, sont primordiales. Le premier critère de performance est le temps de réponse. En effet, il faut pouvoir donner une réponse à l’utilisateur dans un temps acceptable.
Ce temps dépend du problème posé. Par exemple, dans notre système expert de géométrie, le temps de réponse sera acceptable s’il reste de l’ordre de la seconde. Et au vu du nombre de règles, il y a peu de risques d’avoir un temps supérieur.
Dans un système expert médical, ou pour aider un garagiste, là encore le temps n’est pas la priorité tant qu’il reste de l’ordre de quelques secondes.
Cependant, si le système expert doit être utilisé dans un environnement dangereux pour prendre une décision (par exemple pour arrêter ou non une machine) ou doit communiquer avec d’autres systèmes, le temps de réponse va devenir un critère primordial pour la réussite du projet.
En plus du temps de réponse, il existe un deuxième critère de performance : l’utilisation de la mémoire. En effet, la base de faits va grossir au fur et à mesure de l’application des règles. Dans un moteur à chaînage arrière, le nombre de buts à atteindre peut lui aussi prendre de plus en plus de place. Si le système doit être installé sur un appareil possédant peu de mémoire (comme un robot), il faudra donc bien prendre en compte cet aspect.
Enfin, généralement tous les moyens...
Ajout d’incertitudes et de probabilités
Les systèmes experts vus jusqu’ici se basaient sur des règles sûres, et les faits étaient forcément vrais ou faux. Cependant, dans la réalité, les choses sont souvent plus complexes. Il faut donc penser à gérer les incertitudes.
1. Apport des incertitudes
Dans un système expert destiné à identifier des animaux en fonction de caractéristiques physiques, il peut être difficile d’estimer exactement le nombre de doigts aux pattes de l’animal ou la couleur de son ventre. Surtout s’il s’agit d’un prédateur ou d’un animal venimeux, il peut sembler difficile de l’examiner sous tous les angles pour répondre aux questions du système.
Dans ces cas-là, il peut être intéressant d’ajouter de l’incertitude sur les faits : l’utilisateur pourra donc dire qu’il lui semble que l’animal avait le ventre blanc, mais qu’il n’en est pas totalement sûr.
De plus, dans un système expert médical, il paraît dangereux de dire que si les symptômes d’une maladie sont des douleurs dans tout le corps, de la fièvre et une grande fatigue, alors il s’agit forcément d’une grippe. En effet, des maladies plus rares mais plus dangereuses pourraient se cacher derrière...
Domaines d’application
Le premier système expert est apparu en 1965. Nommé Dendral, il permettait de retrouver les composants d’un matériau à partir d’informations sur sa résonnance magnétique et sur le spectrogramme de masse de celui-ci.
Depuis, les systèmes experts se développent dans de nombreux domaines et sont présents jusque dans les logiciels que l’on utilise tous les jours.
1. Aide au diagnostic
Le premier grand domaine d’application des systèmes experts est l’aide au diagnostic. En effet, grâce à leur base de règles, ils vont pouvoir tester et éliminer différentes possibilités jusqu’à en trouver une ou plusieurs probables.
On les retrouve ainsi dans les applications médicales pour aider au diagnostic de certaines maladies. On peut citer MYCIN qui permet de déterminer quelle bactérie se trouve dans le corps d’un patient et quel traitement (type d’antibiotique et posologie) lui administrer pour l’aider à guérir ou CADUCEUS, une extension de MYCIN permettant de déterminer plus de 1 000 maladies du sang. D’autres applications permettent d’aider le diagnostic de maladies à partir de radiographies ou d’images médicales. Plus récemment, on les retrouve dans d’autres applications médicales : détermination de l’âge des os à partir d’une radio (Seok, 2016) ou encore classification des mesures de glycémie dans le cadre du diabète gestationnel (Caballero-Ruiz, 2016).
Ils sont très pratiques pour aider à la recherche de pannes en mécanique (comme dans les voitures) ou en électronique (pour les appareils électroménagers), en limitant les pièces potentiellement défectueuses.
On les retrouve aussi tout simplement dans...
Création d’un système expert en Java
Coder un moteur d’inférences générique et complet en Java est une tâche complexe à réaliser. De plus, il existe des moteurs disponibles (gratuitement ou non) qu’il est facile d’adapter à son problème.
Nous allons cependant nous intéresser à la création du système expert permettant de donner le nom d’un polygone à partir de ses caractéristiques.
Ce système expert sera néanmoins adaptable à d’autres problèmes proches. De plus, le code Java sera portable sur toutes les machines possédant une machine virtuelle (JVM). Les sorties se feront en console.
1. Détermination des besoins
Ce système doit être adaptable à de nombreux problèmes équivalents, de type identification, à partir d’informations entrées par l’utilisateur.
Ici, le système part des données fournies par l’utilisateur pour essayer de déterminer la forme qu’il cherche à reconnaître. Nous n’avons pas de but précis. Un moteur à chaînage avant est donc à préférer pour ce problème, en plus d’être plus simple d’implémentation.
De plus, d’après nos règles, nous aurons deux types de faits :
-
Des faits dont les valeurs seront entières, comme l’ordre du polygone, ou le nombre de côtés de même taille.
-
Des faits dont les valeurs seront des booléens, comme la présence ou non d’un angle droit, ou le fait d’être un triangle.
Notre système expert devra donc prendre en compte ces deux types de faits.
L’utilisateur doit aussi pouvoir facilement utiliser le système expert. Les règles devront donc être écrites dans un langage proche du langage naturel, et l’interface devra être gérée séparément du moteur pour le rendre plus générique (ici on ne fera qu’une interface en mode console).
Enfin, il serait aussi intéressant de connaître le dernier nom trouvé pour la forme et les noms intermédiaires qui ont été utilisés (par exemple, on a utilisé "Triangle", puis "Triangle...
Utilisation de Prolog
Coder un système expert en programmation objet se fait, mais ce n’est pas le paradigme de programmation le plus adapté. Les langages en programmation logique sont faits pour exécuter ce type de tâche. L’écriture de code sera alors plus simple, toute la logique du moteur étant déjà implémentée dans le cœur du langage.
1. Présentation du langage
Prolog, pour PROgrammation LOGique, est un des premiers langages de ce paradigme, créé en 1972 par deux Français, Alain Colmerauer et Philippe Roussel.
Ce n’est cependant pas le seul langage en programmation logique. On peut aussi citer Oz ou CLIPS. Ces langages se rapprochent de ceux de programmation fonctionnelle (LISP, Haskell...) qui peuvent être utilisés pour des systèmes experts.
Prolog contient un moteur d’inférences à chaînage arrière, avec backtracking. On lui donne un but (qui doit être un fait) qu’il va essayer de résoudre. Si ce but contient une variable, alors il cherchera toutes les valeurs possibles pour celle-ci. Si le but contient un attribut, alors il confirmera ou infirmera le fait.
Prolog fonctionne sur la base de prédicats. Chaque prédicat peut être soit un fait avéré, soit un fait inféré grâce à des règles. Par exemple ordre(3) est un prédicat avec un paramètre qui est un fait donné par l’utilisateur. Par contre, nom(triangle) sera un fait inféré par la règle "SI ordre(3) ALORS nom(triangle)".
Le langage contient aussi des prédicats fournis, permettant par exemple d’écrire et lire dans la console de Prolog, de charger un fichier, ou de manipuler des listes.
Dans la suite, nous utiliserons le SWI-Prolog, téléchargeable gratuitement sur le site http://www.swi-prolog.org/ et disponible pour Windows, Mac OS X ou Linux.
2. Syntaxe du langage
Seule la syntaxe nécessaire à la compréhension des exemples est ici fournie. N’hésitez pas à lire la documentation de votre implémentation de Prolog pour en savoir plus. De plus, selon la version utilisée, la syntaxe peut légèrement différer. En annexe se trouve une explication de l’utilisation...
Synthèse
Un système expert permet de partir de faits et d’y appliquer des règles pour obtenir de nouveaux faits, dits inférés. Ils remplacent ou complètent le savoir des experts selon les cas.
Ceux-ci sont composés d’une base de règles indiquant toutes les règles connues de l’expert, et qui permet d’arriver à des déductions. Ils se composent aussi d’une base de faits reprenant tout ce qui est connu de l’utilisateur ainsi que les faits inférés jusqu’ici. Une interface utilisateur permet de communiquer de manière claire avec les différentes personnes utilisant le système.
Le cœur du système expert est son moteur d’inférences. C’est lui qui va choisir et appliquer les règles, et lancer les interactions avec l’utilisateur. Il peut être à chaînage avant s’il part des faits pour en obtenir de nouveaux ou à chaînage arrière s’il part d’un but et cherche comment y arriver.
La création de ce moteur n’est pas toujours chose aisée, mais il est possible d’en implémenter dans tous les langages. Les moteurs à chaînage avant sont cependant bien souvent plus simples à coder, par exemple en Java. Des langages particuliers, issus de la programmation fonctionnelle ou logique, comme Prolog, permettent...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations



