Algorithmes génétiques

Présentation du chapitre

La nature a trouvé le moyen de résoudre certains problèmes en apparence insolubles. La vie est ainsi présente quasiment partout sur Terre, des terres gelées aux fosses sous-marines (présentant des températures et des pressions élevées) en passant par les airs.

Cette réussite s’explique par la puissance de l’évolution biologique. Elle permet d’adapter en permanence les différentes espèces aux milieux à coloniser.

Les informaticiens ont imaginé comment cette évolution pourrait être utilisée pour résoudre des problèmes complexes. C’est ainsi que les algorithmes génétiques sont apparus.

Dans une première partie, les principes sous-jacents à l’évolution biologique sont expliqués. Ils sont nécessaires pour comprendre le fonctionnement global et l’inspiration des algorithmes génétiques.

Ensuite le fonctionnement de ceux-ci sera présenté, tout d’abord de manière globale avec un exemple, puis en revenant sur les principales étapes, avec des bonnes pratiques et les pièges à éviter. La coévolution (l’évolution conjointe de deux espèces) sera aussi expliquée.

Ces algorithmes peuvent être utilisés dans de nombreux domaines...

Évolution biologique

Les algorithmes génétiques sont basés sur l’évolution biologique. S’il n’est pas nécessaire de comprendre tous les détails de celle-ci, il est cependant important de comprendre la source d’inspiration de ces algorithmes.

1. Le concept d’évolution

L’évolution biologique fut étudiée à partir de la fin du 18^e siècle. En effet, les preuves de cette évolution s’accumulaient, et les scientifiques voulaient comprendre les phénomènes sous-jacents.

C’est au début du 19^e siècle qu’est apparue la paléontologie (le terme est employé à partir de 1822), science qui s’intéresse aux fossiles et aux formes de vie aujourd’hui disparues. Les scientifiques trouvaient de nombreux squelettes et les classaient. Ceux-ci présentaient de fortes ressemblances entre eux, ou avec des formes de vie actuelles. Il semblait donc évident qu’il y avait eu une continuité, et que les espèces s’étaient progressivement modifiées au cours des millénaires.

De plus, les sociétés d’élevage étaient nombreuses. On savait depuis longtemps sélectionner les meilleurs individus d’un cheptel pour améliorer la production d’une espèce (comme le lait pour les vaches), ou simplement pour le plaisir. Les races de chiens, de chats ou de chevaux étaient ainsi nombreuses et fort différentes. Il était évident qu’un animal était proche de ses parents, bien que pas totalement identique à ceux-ci, et qu’en sélectionnant les bons parents, on pouvait créer de nouvelles races. Les caniches, les bergers allemands, les cockers et les labradors descendent tous du loup gris (Canis Lupus), domestiqué pendant la préhistoire. C’est l’intervention humaine qui a modelé toutes ces races.

Enfin, les grands découvreurs allaient d’îles en îles, et de nouvelles espèces étaient couramment découvertes. Il apparaissait que les individus situés sur des îles assez proches étaient eux aussi proches physiquement. Au contraire, ils étaient beaucoup plus différents des individus issus d’un autre continent. Les espèces avaient donc évolué de manière différente, mais graduelle.

L’évolution biologique n’était donc plus un tabou au 19e siècle, mais une réalité scientifique. Cependant, il restait à savoir comment cette évolution pouvait avoir eu lieu.

2. Les causes des mutations

Darwin (1809-1882) et Lamarck (1744-1829) s’opposèrent sur les raisons des modifications entre les parents...

Évolution artificielle

L’évolution biologique vue précédemment est dite "désincarnée" : en effet, les principes de reproduction, de survie ou de sélection ne précisent pas comment les informations doivent être stockées ou transmises, ni même ce qui doit évoluer.

Les chercheurs de domaines très divers que ce soit l’économie, la sociologie, la musique... s’y sont donc intéressés. L’informatique n’est pas en reste, et cette évolution biologique peut être utilisée pour créer une évolution artificielle, permettant de résoudre des problèmes que des méthodes plus classiques ne permettent pas de résoudre.

1. Principes

Les algorithmes évolutionnaires vont donc partir d’une population de solutions potentielles à un problème. Chacune est évaluée, pour lui attribuer une note, appelée fitness. Plus la fitness d’une solution est forte et plus celle-ci est prometteuse.

Les meilleurs individus sont ensuite sélectionnés, et se reproduisent. Deux opérateurs artificiels sont utilisés : le croisement entre deux individus, appelé crossover, et des mutations aléatoires.

Une étape de survie s’applique alors pour créer la nouvelle génération d’individus.

Le processus est donc le suivant :

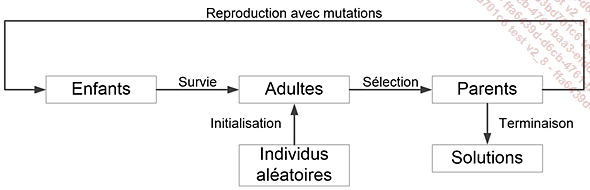
Plusieurs variantes sont apparues dans les années 60 de manière indépendante. Les algorithmes génétiques ont été mis au point par Holland, mais on parle aussi de programmation évolutionnaire (Fogel) ou de stratégies d’évolution (Rechenbert et Bäck). Quelques années plus tard sont apparues l’évolution grammaticale (Ryan, Collins et O’Neill) et la programmation génétique (Koza).

Tous ces algorithmes, souvent rassemblés sous le nom alors générique d’algorithmes génétiques, se basent sur ce principe d’évolution et cette boucle générationnelle. Les différences se trouvent principalement au niveau des représentations et des opérateurs.

2. Convergence

La convergence vers la solution optimale est démontrée théoriquement. Cependant, rien ne précise le temps nécessaire pour converger vers cette solution, qui peut donc être supérieur à ce qui est acceptable.

Il est donc important de bien choisir les différents opérateurs (sélection, mutation, crossover et survie) et les représentations, au nombre de trois : des gènes, des individus et de la population. En effet, ces choix peuvent influencer...

Premières phases de l’algorithme

Avant de passer au calcul des générations, il faut commencer par créer la toute première. Pour cela, il va falloir faire des choix sur les représentations, puis initialiser les individus de la population initiale. De plus, il faudra choisir la fonction d’évaluation de ceux-ci.

1. Choix des représentations

Comme pour beaucoup de techniques d’intelligence artificielle, le choix des représentations est primordial pour limiter l’espace de recherche et pour le rendre le plus adapté possible à l’algorithme choisi.

a. Population et individus

La population contient une liste d’individus. C’est le langage informatique utilisé qui impose parfois la représentation de cette liste. Pour faciliter l’étape de reproduction, il est plus aisé de choisir une structure de données avec un accès direct à un individu, comme un tableau, par rapport à un accès par parcours comme une liste.

Les individus contiennent une liste de gènes. Là encore, le format exact de cette liste est en partie déterminé par le langage. Un accès direct à un des éléments n’est pas obligatoire.

b. Gènes

La représentation des gènes est celle sur laquelle il faut passer le plus de temps. Traditionnellement, il s’agit d’une liste ordonnée de valeurs. Cela signifie que pour tous les individus, le premier gène a la même signification (dans notre exemple précédent, les pions étaient stockés dans l’ordre).

Dans certains cas, il peut cependant être plus adapté de choisir une représentation où la place des gènes est variable, en adaptant les opérateurs. Chaque gène contient alors le nom de la variable associée et la valeur (par exemple, largeur et hauteur pour un objet).

De plus, il est important de bien réfléchir aux variables nécessaires pour résoudre le problème. Il est déconseillé d’avoir trop de valeurs à optimiser et il faut donc vérifier qu’il n’y a pas de variables redondantes, dont les valeurs pourraient être issues des autres.

Enfin, il est plus complexe pour un algorithme génétique de résoudre un problème dans lequel les différents gènes sont liés entre eux. Une analogie peut être celle de la différence entre un mitigeur et un mélangeur. Dans les deux cas, on a un robinet qui permet d’obtenir de l’eau à différentes températures et à différents débits.

Dans le cas du mélangeur, on a deux robinets : un pour l’eau froide et un pour l’eau chaude. Pour...

Création des générations suivantes

Une fois la toute première population créée et évaluée, il faut choisir les différents opérateurs pour passer à la génération suivante :

Sélection des parents parmi les adultes.
Opérateurs de crossover et de mutation pour créer les descendants.
Survie pour créer la nouvelle population à partir des adultes et des descendants créés.

1. Sélection des parents

La sélection consiste à déterminer quels sont les individus qui méritent d’être choisis comme parents pour la génération suivante. Il faut qu’en proportion, les meilleurs parents se reproduisent plus que les parents à fitness plus basse, mais chacun doit quand même avoir une probabilité non nulle de se reproduire.

En effet, c’est parfois en faisant muter ou en croisant des solutions en apparence "mauvaises" que l’on peut trouver une bonne solution à un problème.

Les parents peuvent être sélectionnés de diverses manières, déterministes ou stochastiques. Ce sont les sélections stochastiques (donc faisant intervenir une part de hasard) qui sont les plus utilisées.

Une des solutions les plus courantes est d’utiliser une roulette biaisée : plus un individu est adapté, et plus il aura une grande part sur la roue. Les individus suivants ont donc une part de plus en plus petite. Un tirage au sort indique alors quel est l’individu choisi.

Statistiquement, ceux ayant les fitness les plus élevées auront le plus d’enfants, mais tous ont au moins une chance de se reproduire, même si elle reste faible.

La part -de la roulette de chaque individu peut être déterminée par le rang- de celui-ci le premier ayant toujours la même part par rapport au deuxième ou par sa fitness. Dans ce dernier cas, les proportions changent à chaque génération et un individu beaucoup plus adapté que les autres de sa population aura beaucoup plus de descendants, pour transmettre rapidement ses gènes. Au contraire, dans une population uniforme où les différences de fitness sont faibles, la roulette donnera à peu près à chaque individu la même chance de se reproduire.

La deuxième solution, après la roulette, est d’utiliser le tournoi : deux individus sont choisis au hasard, et c’est le plus adapté qui se reproduira. Les individus les plus adaptés gagneront donc plus souvent les tournois et se reproduiront plus que les individus peu adaptés, mais là encore, tous ont des chances de se reproduire (à l’exception de l’individu le moins adapté qui perdra tous ses tournois)....

Coévolution

La coévolution est un phénomène biologique formalisé en 1964, suite à une étude de deux biologistes sur les liens entre des plantes et certains papillons. En effet, ils ont montré que les deux espèces avaient évolué conjointement : les papillons mangeaient la plante, qui a développé des mécanismes pour se défendre (poison ou protections physiques). Les papillons ont alors développé des moyens de résister à ces poisons ou à ces défenses.

Il s’agit donc d’une course sans fin entre les deux espèces, chacune essayant d’avoir un temps d’avance sur l’autre pour assurer sa propre survie, et ne pouvant arrêter d’évoluer. Les deux espèces en compétition se sont développées et ont évolué plus vite que si chacune avait évolué de manière distincte.

C’est cette coévolution que l’on observe dans tous les systèmes "proies - prédateurs". Ainsi, il existe une course évolutive entre les hackers, qui essaient de percer les sécurités des systèmes informatiques, et les responsables de la sécurité, qui essaient de repousser et d’empêcher les attaques. Chaque camp doit évoluer en permanence, et rapidement, pour essayer...

Domaines d’application

L’équipe de John Holland au sein de l’université du Michigan a commencé à travailler sur les algorithmes génétiques dans les années 60. Cependant, cette technologie n’a commencé à se faire connaître qu’à partir de 1975 avec la publication de son livre.

Les algorithmes évolutionnaires en général ont alors commencé à toucher de nombreux domaines. Pour qu’ils soient efficaces, il suffit de répondre à quelques contraintes :

Le nombre de solutions potentielles doit être très grand.
Il n’y a pas de méthode exacte permettant d’obtenir une solution.
Une solution presque optimale est acceptable.
On peut évaluer la qualité d’une solution potentielle.

Si ces quatre contraintes sont vérifiées, alors un algorithme génétique peut s’avérer être une bonne solution pour trouver une réponse au problème qui, bien qu’elle ne puisse être garantie comme la meilleure, sera en tout cas acceptable, et ce dans un temps raisonnable.

On les retrouve en premier dans les domaines de l’ingénierie et du design. En effet, il est aujourd’hui de plus en plus difficile de créer des pièces répondant aux contraintes et minimisant ou maximisant certaines caractéristiques...

Implémentation

Nous allons maintenant nous intéresser à l’implémentation en C# d’un algorithme génétique générique qui est ici utilisé pour résoudre deux problèmes abordés précédemment :

Le voyageur de commerce, qui consiste à trouver la route la plus courte pour relier un ensemble de villes.
Le labyrinthe, en donnant la suite d’instructions à suivre pour aller de l’entrée à la sortie.

Le code proposé ici et disponible en téléchargement est compatible avec .NET 4.5 et supérieur, ASP.Net 1.0, et Windows 8 et supérieur. Le programme contenant la fonction Main est une application console pour Windows.

1. Implémentation générique d’un algorithme

a. Spécifications

Nous voulons coder un moteur générique pour un algorithme génétique, qui est ensuite appliqué à deux problèmes différents, en écrivant le moins de code possible pour passer de l’un à l’autre.

Il est donc important de bien fixer les besoins. Le processus évolutionnaire en lui-même, le cœur du système, s’occupe d’initialiser la population, puis lance l’évaluation, la sélection des parents et la création des descendants et enfin la survie. On reboucle ensuite sur l’évaluation, et ce jusqu’à ce qu’un critère d’arrêt soit atteint.

On va donc définir deux critères d’arrêt possibles : on a atteint la fitness que l’on voulait ou on a atteint le nombre maximum de générations. Dans les deux problèmes, il s’agit de minimiser la fonction d’évaluation : le nombre de kilomètres pour le voyageur de commerce ou la distance à la sortie pour le labyrinthe. On fixe donc une fitness minimale à atteindre.

On pourrait tout à fait adapter l’algorithme pour lui permettre de maximiser la valeur d’adaptation, mais comme nos deux problèmes cherchent à minimiser la fitness, nous ne le ferons pas ici.

Les différents paramètres de l’algorithme sont définis dans une classe à part. Nous avons ensuite des interfaces ou classes abstraites pour les individus et les gènes. En effet, ce sont les deux seules classes qu’il faut redéfinir pour chaque cas. Pour le problème de sortie du labyrinthe, nous avons besoin d’avoir des génomes de taille variable (la liste des instructions), l’algorithme doit donc permettre de le gérer.

Pour alléger le cœur du système de la gestion du cas à résoudre, nous déportons dans une fabrique la création des individus...

Synthèse

Les algorithmes génétiques (ou plus généralement les algorithmes évolutionnaires) sont inspirés des différentes recherches menées en biologie sur l’évolution.

On a alors une population d’individus, chacun composé d’un génome qui est une liste de gènes. Ces individus sont évalués par rapport à la qualité de la solution à un problème donné qu’ils représentent (ce qu’on appelle son phénotype).

Les meilleurs individus sont sélectionnés pour être des reproducteurs. De nouvelles solutions sont alors créées, à partir d’un ou plusieurs parents. Dans le cas où plusieurs parents interviennent, on réalise un crossover, c’est-à-dire un croisement entre les informations génétiques des différents parents.

Les génomes des descendants subissent ensuite des mutations aléatoires, représentant les erreurs de copie qui ont lieu lors de la reproduction. Chaque descendant, bien que proche de ses parents, en est donc potentiellement différent.

Cette nouvelle génération doit ensuite survivre, pour faire partie de la population de la génération suivante. On reboucle le processus jusqu’à atteindre des solutions optimales ou quasiment optimales....