Itération

Introduction

Un traitement itératif est un traitement fait ou répété plusieurs fois selon le « Petit Larousse ». Ce terme est synonyme de fréquentatif qui se dit d’un verbe qui marque une action fréquemment répétée, comme clignoter (...). Dans ce chapitre, nous construisons des algorithmes de transformation au cours desquels le système passe de l’état initial à l’état final en traversant une succession finie d’états caractérisés par une propriété commune. Nous montrons comment construire ce type d’algorithmes d’une façon raisonnée et systématique.

La section « Premiers exemples de construction d’itérations » introduit la méthode par quelques exemples simples. La section « Itérer dans un tableau » étudie différentes situations dans lesquelles l’itération est utilisée sur les composantes d’un tableau. La section « Algorithme ou programme ? » est une discussion justifiant la méthode étudiée dans ce livre et propose des exercices d’application au cours desquels il devient possible de donner des solutions itératives à des exercices parfois déjà résolus précédemment....

Premiers exemples de construction d’itérations

Ces exemples sont simples. Le premier, la construction d’une table de multiplication, est même trivial. C’est qu’il s’agit d’un premier exposé pour introduire les raisonnements permettant de construire une itération : il faut éviter de multiplier les difficultés. C’est pourquoi on commence par se concentrer sur les étapes de la construction et du raisonnement sur un problème élémentaire. Le second exemple explore un tableau dont les données sont des instances d’un type structuré. La section se termine ensuite par quelques exercices d’application de même nature.

... 
constante 
    MIN : ENTIER 0  # Numéro de la première case du tableau 
    MAX : ENTIER 10 # Numéro de la dernière case 
 variable  
    table : TABLEAU[ENTIER][MIN, MAX]  
... 

... ...

Explorer un tableau

Un CLIENT est une PERSONNE identifiée par un numéro entier. Une PERSONNE possède une ADRESSE et une IDENTITÉ. Le diagramme ci-dessous représente ces entités et leurs associations mutuelles.

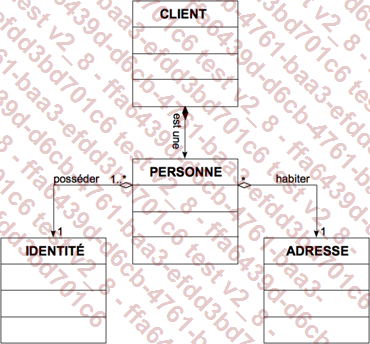
Remarquez la nature particulière de l’association entre CLIENT et PERSONNE. On indique ainsi qu’une instance de CLIENT est composée d’une et d’une seule instance de PERSONNE. En toute rigueur, il faudrait utiliser ici l’association d’héritage, mais nous ne sommes pas en algorithmique objet. De plus, la couleur du losange du côté CLIENT indique que, lorsque le client disparaît, la personne disparaît avec lui. La discussion sur les différentes associations et leur signification a déjà été abordée au chapitre « Structures élémentaires », dans la solution de l’exercice n°11, développée dans les éléments en téléchargement disponibles depuis la page Informations générales.

Le type CLIENT est défini par la déclaration :

type 
    CLIENT 
structure 
    numéro : ENTIER 
    p      : PERSONNE 
fin CLIENT 

La déclaration du type PERSONNE est de même :

type 
    PERSONNE 
structure 
    identité : IDENTITÉ 
    âge      : ENTIER 
    adresse  : ADRESSE 
fin PERSONNE 

Enfin, le type ADRESSE a déjà été utilisé au chapitre « Structures élémentaires ».

Un tableau, qui peut contenir jusqu’à 1000 CLIENTS a été déclaré et initialisé :

constante  
    MAX_CLIENTS : ENTIER 1000  
    MIN_CLIENTS : ENTIER 1  
    VIDE   : ENTIER ??? # Numéro d'un client qui n'existe pas 
    EFFACÉ : ENTIER ??? # Numéro d'un client effacé 
...  
variable  
    clients : TABLEAU[CLIENT][MIN_CLIENTS, MAX_CLIENTS]  
... 

Actuellement, toutes les cases n’ont pas nécessairement été initialisées...

Algorithme ou programme ?

Nous en savons suffisamment à présent pour revenir sur quelques notions qui ont déjà été abordées dans les chapitres « Qu’est-ce que l’algorithmique ? » et « Programmes directs ». Qu’est-ce qu’un algorithme ? Qu’est-ce qui le distingue d’un programme destiné à un ordinateur ? Construire un programme et définir un algorithme sont-elles des activités distinctes, chacune développant ses propres méthodes, ou ne constituent-elles que les « deux faces de la même médaille » ? Cette section ne cherche pas à répondre de façon définitive. On y expose seulement quelques idées simples qui complètent la vision partielle des chapitres précédents. La première partie développe un exemple recopié d’un livre qui traite d’algorithmique. La seconde partie expose l’une des solutions préconisées pour le problème.

VAR 
    marques  : TABLEAU[1 .. 100] de RÉEL ; 
    nombres  : ENTIER ; 
    somme, i : ENTIER ; 
    moyenne  : RÉEL   ; 
DÉBUT 
    (* Remplir le tableau *) 
    i := 1 ; 
    écrire("Donner un entier : ") ; 
    lire(marque[i]) ; 
    TANT QUE(marques[i] < > - 1) 
      DÉBUT   
        i := i + 1 ; 
        écrire("Quel est l'entier suivant ? ") ; 
        lire(marques[i]) ; 
      FIN ; 
    (* Calculer la moyenne *) 
 ...

Exercices d’application

Cette section propose des exercices d’application variés. Le premier exercice étend l’étude commencée au chapitre « Structures élémentaires ».

On veut conserver l’histoire des mouvements mensuels sur un compte courant.

1. Modifier le type COMPTE défini au chapitre « Structures élémentaires » pour garder la trace des mouvements sur un compte pendant un mois.

2. Établir le solde en fin de mois d’un compte donné.

Le solde n’est plus un attribut du compte. Il est obtenu en parcourant l’historique mensuel et l’historique annuel qui enregistre le montant du solde du compte pour chaque mois.

3. Refaire les définitions précédentes.

Un tableau clients contient les comptes courants d’un ensemble de clients.

4. Déterminer les clients pour lesquels la moyenne des montants des mouvements est supérieure à une somme donnée.

L’exercice suivant sera complètement résolu au chapitre « Édition d’un nombre ».

1. Écrire un algorithme itératif qui transforme un entier n quelconque en sa représentation dans une base B ≥ 2 quelconque.

Lorsque la base est supérieure à 36, on peut utiliser la représentation des chiffres en utilisant la base dix, mais en séparant chaque chiffre de la représentation du nombre en base B par un séparateur convenu, par exemple un point. C’est ce qui est pratiqué pour noter, par exemple, l’adresse IP d’un hôte sur un réseau en IPv4. Ainsi, par exemple, la représentation en base 256 de 3000, exprimée ici en base dix, s’écrira : 11.184₂₅₆ = 3000_dix.

Cet exercice est entièrement résolu au chapitre « Édition d’un nombre ».

On donne une chaîne de caractères dont différentes parties sont séparées par un caractère SÉPARATEUR particulier. L’exemple ci-dessous représente une telle chaîne, dans laquelle le caractère séparateur est le caractère...