Programmes directs

Introduction

Ce chapitre présente la notion d’algorithme comme la description d’un procédé composé d’une succession d’opérations. À partir d’exemples simples tirés de l’expérience quotidienne de chacun et pas nécessairement dans le domaine de l’informatique, on dégage une idée intuitive de ce qu’est un algorithme et on commence à en écrire d’une façon informelle. Une série d’exercices permet ensuite de s’entraîner à élaborer des descriptions dans des domaines variés.

La section « Premiers exemples » introduit quelques exemples. La section suivante définit informellement un algorithme comme une suite d’instructions destinées à la machine abstraite. On peut alors commencer à introduire les spécifications dans la section « Spécifications » et écrire les premiers algorithmes à la section « Premiers algorithmes ». Les deux sections suivantes sont des exercices. Ils sont accompagnés d’une solution développée dans la section « Exercices résolus » et sont énoncés sans solution dans la section « Exercices ». On termine le chapitre par quelques notes bibliographiques....

Premiers exemples

Exemple 1 : Préparation d’une marinade

Dans un vieux livre de cuisine, je lis la recette suivante, en page 41 :

« MARINADE

Thym - laurier - persil - ail - huile - vinaigre - sel - poivre.

Mettez dans un plat 2 volumes d’huile, pour 1 de vinaigre, le thym, le laurier, le persil, l’ail haché finement, salez, poivrez et faites baigner dans cette préparation la viande que vous voulez faire mariner. Vous pouvez laisser mariner 2 à 6 jours, mais chaque jour ajouter de l’huile et du vinaigre. Pour le poisson, vous pouvez remplacer le vinaigre par du jus de citron. »

Cette recette décrit un algorithme : comment réaliser une marinade ? À partir d’ingrédients précisés, elle décrit une succession d’opérations qui les utilisent pour obtenir un résultat. Elle pourrait énumérer les différentes opérations en les ordonnant :

1. mélanger dans un plat 2 volumes d’huile à 1 volume de vinaigre ; pour du poisson, remplacer le vinaigre par du jus de citron ;

2. hacher finement l’ail ;

3. ajouter à la vinaigrette le thym, le laurier, le persil et l’ail haché ;

4. saler et poivrer ;

5. placer la viande à faire mariner dans cette préparation ;

6. pendant 2 à 6 jours, ajouter chaque jour de l’huile et du vinaigre.

Exemple 2 : L’addition de deux entiers

Tout élève apprend à additionner deux nombres entiers positifs en classe primaire. Pour calculer la somme de 127 et 35, il apprend à « poser » l’addition, en plaçant en colonnes les chiffres des deux nombres, les unités...

Définition informelle d’un algorithme

Un algorithme est la description d’un procédé. Il décrit une succession d’opérations élémentaires, exprimées dans un langage donné, à exécuter dans un certain ordre. L’exécution n’est possible que lorsque certaines conditions sont remplies. L’ail n’est ajouté que lorsqu’il a été haché ; on ne peut calculer le niveau de déclenchement q_d que lorsque la moyenne m_v des ventes quotidiennes a été obtenue. L’exécution des opérations élémentaires dont il s’agit permet de faire passer le système considéré, d’un état initial I, représenté par les valeurs des attributs donnés, à un état final F, représenté par les nouvelles valeurs des attributs et les résultats à obtenir. Pour l’addition, les attributs donnés sont les deux entiers a et b dont les valeurs sont respectivement 127 et 35. L’état initial est représenté par ces deux valeurs. Le résultat est 162 et l’état final est représenté par les trois valeurs 127, 35 et 162. La figure ci-dessous représente les deux états et la transition qui fait passer de l’un à l’autre.

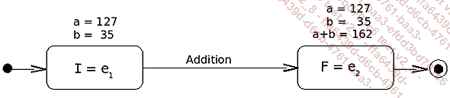
L’état initial I ou e₁ est caractérisé par les valeurs 127 et 35 de a et b, respectivement. L’état final F ou e₂ est caractérisé par ces mêmes valeurs 127 et 35 et par la valeur 162 de la somme de a et b.

De même, l’état initial I de l’exemple de gestion de stock est constitué des valeurs des attributs q_s, d_r et v₁, v₂, ..., v₁₂. L’état final F est représenté...

Spécifications

Une tâche importante, quand on cherche à écrire un algorithme, consiste à le spécifier. Il s’agit de dire, de la façon la plus précise possible, ce que fait l’algorithme et, cela, sans exprimer comment il le fait. En ce sens, spécifier un algorithme, c’est poser formellement le problème qu’il résout, comme l’ont montré les sections précédentes de ce chapitre. C’est une étape difficile, mais indispensable pour clairement définir l’algorithme et ses effets. Cette section introduit, par quelques exemples et exercices résolus, cette étape de spécification. Elle est complétée dans la suite du livre, à mesure que nous construirons les outils nécessaires. 

Cette étape de spécification est, en fait, l’unique objet d’étude de ce livre. Accessoirement, le livre montre aussi comment réaliser des algorithmes simples, mais uniquement quand les étapes de leur construction mettent en évidence leur conformité aux spécifications. On prépare ainsi l’étape de la preuve de l’algorithme, mais cette étape dépasse les objectifs de ce livre. Étudions un exemple.

On considère un feu qui règle la circulation à un carrefour.

Écrire l’algorithme qui détermine la couleur du feu lors du prochain changement.

Solution

Un tel feu signale l’état de la circulation qu’il règle par trois couleurs : vert, orange et rouge. Les couleurs s’enchaînent dans cet ordre à une cadence fixée. Lorsque la couleur est rouge, le changement refait passer le feu au vert. On ne s’intéresse qu’au changement de couleur, autrement dit, à l’opération qui fait passer de l’une à l’autre, dans l’ordre précisé.

Supposons que nous disposons d’une opération, désignée par successeur, qui prend en entrée une couleur de l’ensemble C = {rouge ; vert ; orange} et qui retourne son successeur dans la suite ordonnée (vert ; orange ; rouge). Avec ces hypothèses, l’algorithme s’écrit de cette manière...

Premiers algorithmes

Cette section complète la précédente en montrant, sur quelques exemples élémentaires, les notations utilisées pour dire comment un algorithme effectue son calcul, autrement dit, comment assurer la transition de l’état initial I à l’état final F du système logiciel. On en reste encore, comme dans tout ce chapitre, à des idées intuitives, non formalisées, mais pourtant rigoureuses. Ici aussi, la méthode est exposée à partir d’exercices résolus.

Cet exercice reprend l’étude de l’exemple 4 commencée au début de la section « Définition informelle d’un algorithme ».

Écrire les instructions qui résolvent le problème posé.

Solution

Il s’agit donc d’étudier quelles sont les transitions qui feront passer le système logiciel de son état initial I, dans lequel sont connues les valeurs des données d’entrée du problème, à l’état final F dans lequel on sait s’il faut ou non lancer un réapprovisionnement. Nous avons vu, lors de l’étude préliminaire de cet exemple, que les étapes du calcul s’organisent selon le plan suivant :

Cet algorithme résout le problème et il est complet si on sait calculer une moyenne. Pour réussir à présenter la solution de problèmes plus complexes, pour lesquels cette forme simple d’écriture en langage naturel n’est pas adaptée, nous allons écrire la solution trouvée en utilisant un formalisme un peu plus restrictif que le langage naturel.

Il s’agit donc, à présent, de dire comment sont effectués les calculs de chaque étape pour prendre la décision.

On obtient la moyenne m_v des ventes quotidiennes en divisant le total des ventes sur l’année par le nombre de jours ouvrables....

Exercices résolus

Cette section propose quelques exercices qui demandent un peu plus de réflexion. Il s’agit de préparer des solutions complètes et définitivement prêtes pour l’étape d’implémentation, même si un même problème peut donner lieu à différentes solutions toutes correctes. Ces propositions de solutions sont élaborées à la suite de chaque énoncé. Pour chacune d’elles, les notations sont complétées par les notions nécessaires à leur expression. Cependant, le lecteur est invité à réfléchir à ces problèmes, à les spécifier et, éventuellement, à les résoudre d’une façon informelle, par exemple en rédigeant les solutions « en français » avant d’étudier les solutions proposées.

On donne deux variables quelconques, d’un type T qui n’est pas précisé.

1. Écrire l’algorithme qui échange les valeurs de ces deux variables.

Soient V₁ la valeur de la donnée contenue dans la variable v₁ et V₂ la valeur dans v2. Lorsque l’algorithme se termine, la donnée contenue dans la variable v₁ doit avoir la valeur V₂ et celle contenue dans v2 doit avoir la valeur V₁.

Indication: on donne une bouteille remplie d’eau et une autre bouteille remplie de vin. Comment échanger les contenus des deux bouteilles sans les mélanger ?

L’indication qui précède suggère d’utiliser une variable intermédiaire pour résoudre le problème. Peut-on faire autrement ? C’est l’objet de la question suivante.

On suppose que les objets de type T auxquels appartiennent les valeurs des variables v₁ et v₂ peuvent être additionnés ou soustraits. C’est le cas des nombres entiers ou réels par exemple.

2. Même question que la précédente, mais l’algorithme proposé ne fait que des additions et des soustractions, sans utiliser d’autre variable que v₁ et v₂.

Solution

On peut commencer par spécifier l’algorithme. C’est ce qui est fait ci- dessous. Remarquez qu’il s’agit de modifier les données...

Exercices

Les solutions des exercices proposés ne font intervenir aucune notion nouvelle. Seules les quelques notions étudiées dans ce chapitre sont nécessaires pour donner une solution complète à ces exercices, même si, parfois, il existe une solution meilleure que celle actuellement accessible. Chaque exercice doit être entièrement spécifié, la réalisation de l’algorithme proposé doit être complète et, s’il y a lieu, démontrée. Certains énoncés sont volontairement imprécis et donc permettent, parfois, différentes interprétations. Les algorithmes, pour les résoudre, doivent être parfaitement définis et ne laisser subsister aucune ambiguïté. Il faudra donc faire des choix qui sont laissés à la discrétion du lecteur, mais qui doivent être clairement énoncés, si ce n’est justifiés.

1. Écrire un algorithme qui calcule le prix toute taxe comprise (TTC) pour un prix hors taxe et un taux de TVA donné.

2. Écrire un algorithme qui calcule le montant des intérêts rapportés par un capital placé à un taux donné pendant une durée donnée, exprimée en mois.

Résumé

Ce chapitre a abordé l’écriture d’algorithmes. Un algorithme est la description d’un procédé de calcul composé d’une succession d’opérations. Une fonction calcule un résultat à partir de données qu’elle ne modifie pas. Une procédure modifie un état en calculant les nouvelles valeurs des données.

L’élaboration d’un algorithme se décompose en deux phases qui ne doivent pas être confondues. La spécification précise ce que fait l’algorithme sans dire comment il le fait. La spécification d’un algorithme fait partie de sa documentation. Elle est composée de la signature du module logiciel, de la précondition et de la postcondition. La définition de l’algorithme exprime par des instructions comment il réalise son calcul.

La précondition regroupe les conditions que doivent satisfaire les données en entrée pour que l’algorithme calcule ses résultats. Elles doivent être simultanément VRAIES pour que l’algorithme effectue un calcul « juste » pour produire les résultats attendus. C’est de la responsabilité du client logiciel des services de l’algorithme d’assurer la réalisation de ces conditions. La postcondition exprime les garanties qu’apporte...