Crypter
Introduction
On s’intéresse à la sécurité des données d’un système informatique. C’est un problème vaste, difficile, qui revêt de multiples aspects. Ici, nous étudions et mettons en pratique d’une façon simplifiée quelques-uns de ces aspects.
La deuxième section étudie comment assurer l’intégrité des données. Il s’agit de vérifier que les données mises en œuvre n’ont pas subi de modification. La section suivante aborde les techniques qui assurent la confidentialité des données. On veut ainsi ne permettre l’accès aux données qu’à un nombre restreint d’entités utilisatrices bien caractérisées. Nous devrions ensuite nous intéresser aux méthodes pour identifier, authentifier et autoriser les entités qui accèdent aux données mais ce livre n’aborde pas ces aspects du problème.
Intégrité
1. Présentation
Les données auxquelles nous nous intéressons « contiennent » une certaine « information ». Toute perturbation des données va modifier cette information.
Les perturbations peuvent être de différentes natures. Ainsi, par exemple, lors d’écritures ou de lectures vers ou depuis un disque, l’environnement électromagnétique du système peut modifier les données d’une façon imprévisible pendant leur transfert. De même, pendant un échange de données sur un réseau, un utilisateur peut intercepter et modifier les messages d’une façon illégitime ou inattendue. Une application peut corrompre les données sur lesquelles elle travaille, à la suite d’un incident de fonctionnement par exemple.
Les méthodes usuelles auxquelles nous nous intéressons dans cette section permettent de s’assurer que les données conservent « l’information qu’elles contiennent ». Nous voulons ainsi nous convaincre que les données n’ont pas subi de modification. Il s’agit donc de s’assurer de l’intégrité des données utilisées. Le principe général d’une telle méthode est illustré par la figure ci-dessous.
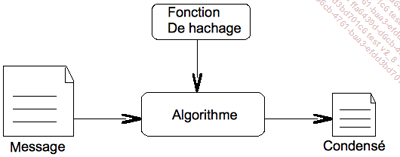
Un algorithme calcule un condensé ou empreinte (hash) du message. Quelle que soit la taille du message, le condensé aura une longueur fixe, par exemple de 32 octets (256 bits). Ainsi, toute l’information contenue dans le message sera comprimée, « condensée » en 32 octets.
Pour s’assurer que les données n’ont pas été perturbées, on recalcule, avec le même algorithme, le condensé du message à vérifier et on le compare au condensé original. Le détail des opérations est donc :
-
recalculer le nouveau condensé ;
-
comparer le nouveau condensé au condensé original ;
-
s’ils sont différents, c’est que les données ou le condensé original ont subi des modifications.
Cette méthode est illustrée par la figure suivante.
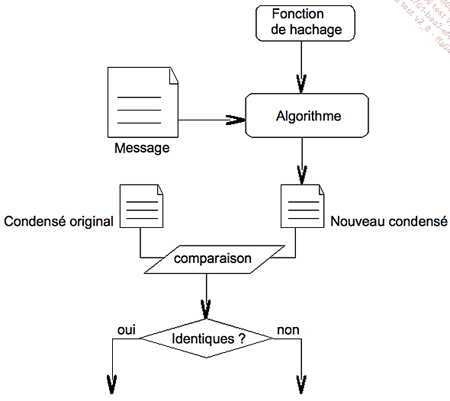
Sur cette figure, le condensé original est le condensé envoyé par l’émetteur...
Confidentialité
On cherche, cette fois, à s’assurer que les seules entités qui pourront prendre connaissance des données sont celles prévues. Le principe consiste à masquer les données afin qu’elles ne soient plus directement compréhensibles par toute autre entité que l’entité destinataire. On parle alors de cryptage des données.
1. Principes mathématiques de la confidentialité
Soient M l’ensemble des messages en clair, C l’ensemble des messages cryptés et K l’ensemble des clés de chiffrement. L’opération de chiffrement est une fonction S de M x K dans C :
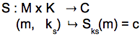
Le déchiffrement est une fonction D de C x K dans M :
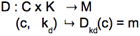
Les clés de chiffrement/déchiffrement sont ks et kd respectivement. Les deux fonctions vérifient : Dkd(Sks(m)) = m. Cette formule exprime que le chiffrement est réversible. On peut représenter ces opérations comme sur le dessin de la figure ci-dessous.
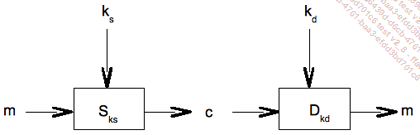
Les algorithmes de chiffrement utilisent différentes relations mutuelles entre ks et kd.
2. Cryptographie à clé secrète
Lorsqu’il existe un moyen simple d’obtenir kd à partir de ks, on parle de chiffrement symétrique ou encore de chiffrement à clé secrète. Dans ce cas, les deux extrémités partagent un secret commun. Ce peut être, par exemple, la même valeur de clé k = ks = kd. Toute entité qui connaît k peut alors déchiffrer le message c pour obtenir le message m.
On sait, en théorie, assurer une confidentialité parfaite avec ce type de cryptage où les entités qui communiquent partagent un secret commun. Cependant, cette confidentialité parfaite n’est obtenue qu’au prix de conditions préalables irréalisables. L’algorithme de Vernam est particulièrement simple et assure le secret parfait des échanges à ces conditions. Voyons cela.
 k,
dans laquelle
k,
dans laquelle  désigne l’opérateur
booléen...
désigne l’opérateur
booléen...Notes bibliographiques
L’essentiel de ce chapitre est inspiré de [MAR04]. C’est un livre difficile pour une initiation mais une référence rigoureuse pour une introduction aux techniques de chiffrement. Le protocole d’échange de l’exercice 2 est extrait d’un cours personnel. L’exercice sur le codage mono-alphabétique simple est inspiré d’un exercice publié par le CERTA. L’exercice sur le codage de Vigenère est inspiré d’un ancien article paru dans la revue MICRO-SYSTÈMES disparue depuis déjà de nombreuses années.
Conclusion
La sécurité des données doit assurer leur intégrité, la confidentialité des échanges et l’identification/authentification des entités qui réalisent ces échanges. Ce chapitre a exposé quelques idées simples pour vérifier l’intégrité ou pour assurer la confidentialité des échanges. Les principes ont été présentés à partir de méthodes élémentaires qui ne sont pas utilisables en l’état, mais qui donnent une idée juste de la réalité. Le domaine est cependant bien plus vaste et difficile que ne peut le laisser penser cette présentation, dont le seul objectif était de fournir un contexte pour étudier quelques algorithmes.
Bibliographie
[MAR04] Bruno MARTIN : Codage, cryptologie et applications ; PRESSES POLYTECHNIQUES ET UNIVERSITAIRES ROMANDES, 2004.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
