Du bon usage des fonctions objectifs

Raison d’être des fonctions objectifs

Les fonctions objectifs sont centrales dans la construction des arbres de décision avec la méthode du Gradient Boosting.

En effet, comme l’a montré le chapitre Gradient Boosted Tree : fonctionnement, toute la méthode du Gradient Boosting est basée sur les fonctions objectifs. 

Le choix de la feature retenue lors de la construction d’un nœud se fait par le biais du gain, dont le calcul dérive de la fonction objectif à travers son gradient et sa hessienne. Sa valeur se calcule en faisant la différence entre l’objectif courant d’un node et les objectifs atteints par l’ajout de deux nouveaux nœuds. La formule utilisée est la suivante :

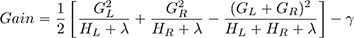
Le rôle de la fonction objectif est donc primordial pour la constitution d’une collection d’arbres de décision.

Dans le même esprit, l’objectif est l‘acteur essentiel de la prédiction en elle-même, puisque c’est lui qui définit la valeur des poids associés à chaque feuille. Pour rappel, la formule qui permet de les calculer est la suivante :

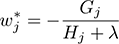
Là encore, la fonction objectif est impliquée à travers son gradient et sa hessienne. Maîtriser les fonctions objectifs est indispensable, et l’objet de ce chapitre est justement de se familiariser en profondeur...

Objectifs usuels

Les trois principales librairies de Gradient Boosting, XGBoost, CatBoost et LightGBM offrent toutes trois une petite dizaine de possibilités comme choix de fonction objectif.

Les sections qui suivent vont présenter les plus employées, selon le cas d’usage : régression ou classification.

1. Classification

La classification nécessite des fonctions objectifs spécifiques, en raison de la nature discrète des prédictions. Contrairement à la régression, les valeurs possibles en sortie ne forment pas un continuum, mais un ensemble discret.

Cette particularité doit être prise en compte dans les fonctions objectifs, notamment en ce qui concerne la double dérivabilité qui est nécessaire pour le Gradient Boosting.

a. Fonction logistique

L’objectif basé sur la fonction logistique est utilisé pour les classifications binaires. La fonction logistique s’appuie en réalité sur deux fonctions : la sigmoid et la log loss.

La sigmoid est utilisée pour « binariser » la sortie de la prédiction. Appliquée à la prédiction brute, elle lui donne la forme suivante :

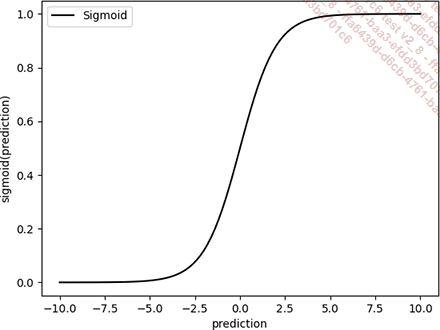
Elle s’assure donc que, en dehors de la zone de transition, les valeurs en sortie sont bien 0 ou 1.

Elle est définie par cette formule : 

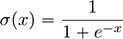
La classification étant binaire et la sigmoïde...

Objectifs régularisés

Cette stratégie visant à rendre dérivable une fonction qui ne l’est pas s’appelle une régularisation. Le principe est de trouver une formule qui permet de calculer de manière quasi exacte le résultat d’une fonction non régulière.

Les deux fonctions suivantes sont un exemple de ce qui peut être fait pour la fonction erreur absolue, qui revient régulièrement comme objectif.

1. Logcosh

Dans un premier temps, il est intéressant de construire une approximation de l’erreur absolue. La Pseudo Huber Loss vue ci-dessus est une possibilité, mais comme le montre son tracé, elle s’écarte un peu du tracé de l’erreur absolue.

Pour obtenir une meilleure approximation, il est possible d’utiliser la formule suivante, basée sur la combinaison du logarithme et du cosinus hyperbolique : 

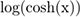
Son tracé est donné par la courbe suivante :

Son implémentation en Python est triviale :

import math 
 
def logcosh(err): 
    loss = math.log(math.cosh(err)) 
    return loss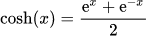 

Pour bien comprendre pourquoi cette formule donne une bonne approximation de l’erreur absolue, il est très éclairant de rentrer dans le détail de la formule du cosinus hyperbolique : 

Lorsque x est suffisamment...

Objectifs personnalisés

Ces différentes fonctions n’étant pas fournies par défaut par les implémentations courantes du Gradient Boosting pour les arbres de décision, cette section va montrer comment elles peuvent être intégrées. En particulier, le cas de XGBoost va être approfondi.

Cette section montrera aussi un usage astucieux des fonctions quantiles pour prédire des intervalles de confiance.

import pandas as pd 
import numpy as np 
from xgboost.sklearn import XGBRegressor 
from sklearn.model_selection import ShuffleSplit 
import matplotlib.pyplot as plt 
 
 
# La fonction log cosh quantile est une version régularisée de la  
# fonction de régression quantile 
def log_cosh_quantile(alpha): 
    def _log_cosh_quantile(y_true, y_pred): 
        err = y_pred - y_true 
        err = np.where(err < 0, alpha * err, (1 - alpha) * err) 
        grad = np.tanh(err) 
        hess = 1 / np.cosh(err)**2 
        return grad, hess 
    return _log_cosh_quantile