Gradient Boosted Tree : fonctionnement
Méthodes ensemblistes
Après l’aperçu haut niveau offert par le premier chapitre sur les méthodes de Gradient Boosting appliquées aux arbres de décision, cette section va être l’occasion de rentrer dans le vif du sujet, en détaillant les principes et méthodes sur lesquels elles s’appuient.
Après un rappel des motivations justifiant l’usage des modèles ensemblistes et de leur construction avec une approche de type Gradient Boosting, ce chapitre abordera le fonctionnement des arbres de décision. Ce sont les modèles de base des méthodes de type Gradient Boosted Tree.
La section sur le Gradient Boosting présentera les fondements mathématiques de cette approche et proposera une implémentation en Python pour les arbres de décision. Coder leur fonctionnement, aussi bien pour l’entraînement que la prédiction, permettra de donner corps à ces explications théoriques.
1. Principes et motivations
Les modèles de type Gradient Boosted Tree sont à classer dans la catégorie des méthodes ensemblistes.
Le parti pris de ces méthodes est de construire des modèles complexes en combinant des ensembles de modèles plus simples. Le modèle ainsi obtenu est nommé prédicteur fort (strong learner), tandis que les sous-modèles le composant sont...
Arbres de décision
Les arbres de décision sont les prédicteurs faibles utilisés par les modèles de type Gradient Boosted Trees présentés dans cet ouvrage. C’est en les combinant qu’ils constituent un prédicteur fort. Les paragraphes qui suivent détaillent leur fonctionnement et donnent une première implémentation simple en Python.
1. Principes et motivations
Les arbres de décision sont une structure de données, somme toute simple, mais très puissante, qui permet, comme son nom le laisse présager, d’accéder à une valeur sur la base d’une série de décisions.
À chaque nœud de l’arbre est associée une décision. Ces décisions, n’appelant qu’une réponse positive ou négative, sont binaires. Chaque nœud a de ce fait deux nœuds fils. Ce sont donc des arbres binaires. Ces nœuds peuvent être une feuille ou à nouveau une autre décision.
Le schéma suivant illustre ce principe pour un arbre permettant de comparer des données constituées de deux colonnes : A et B.
Suivant la valeur de ces deux colonnes, les valeurs prédites seront 2, 4, ou 6.
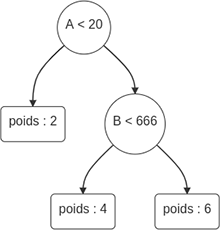
Par convention, et dans tout le reste de cet ouvrage, les arbres binaires seront à interpréter comme suit :
-
Les nœuds sont représentés par des cercles.
-
Les feuilles sont des rectangles.
-
Les nœuds contiennent un test binaire. Si le test est positif, le parcours de l’arbre se continue sur la branche de gauche. S’il est négatif, le parcours se continue sur la droite.
-
Les feuilles contiennent les poids, c’est-à-dire les valeurs prédites.
Il est important de remarquer que la profondeur d’un arbre de décision, à travers le nombre de feuilles, va gouverner la cardinalité de l’espace de prédiction. Les arbres de décision sont donc des systèmes discrets, qui ne prédisent qu’un nombre fini de valeurs. C’est à opposer aux méthodes de prédiction dérivées des méthodes de régression linéaire, qui génèrent des prédictions continues.
Le tableau ci-dessous éclaircit le fonctionnement de cette structure...
Gradient Boosting
La structure, la création et le parcours d’un arbre de décision ayant été décrits ci-dessus, cette nouvelle section va détailler comment construire et combiner ces prédicteurs faibles pour construire un prédicteur fort.
Cette construction et cet assemblage sont la partie complexe lors de la construction d’un modèle selon la méthode du Gradient Boosted Tree : il faut identifier les critères de décision pour chaque nœud, calculer la valeur optimale pour chaque feuille, puis recommencer pour le prédicteur suivant.
C’est la phase d’apprentissage du modèle. Elle doit ingérer les données de l’ensemble d’entraînement et en retirer les paramètres optimaux.
Les paragraphes suivants vont être l’occasion de rentrer dans les principes et méthodes mathématiques qui sont mis en œuvre pour assurer cette construction.
1. Principe du boosting
Les méthodes de Gradient Boosting dérivent, comme leur nom le présage, de la méthode de boosting.
Le principe du boosting, qu’il est possible de traduire en français par « amélioration », consiste en deux points :
-
Combiner séquentiellement des modèles faibles pour construire un modèle fort.
-
Entraîner chacun de ces modèles sur une version modifiée des données d’entraînement.
L’originalité de cette approche réside essentiellement dans le second point, l’idée étant de focaliser le nouveau prédicteur là où les précédents péchaient par manque de précision.
Cela se fait généralement en donnant plus de poids durant l’apprentissage aux échantillons de données pour lesquels l’erreur est importante. D’autres traitements peuvent être appliqués pour altérer les données entre les entraînements successifs. Utiliser le gradient d’une fonction d’erreur est l’un d’entre eux, et celui sur lequel repose le Gradient Boosting.
Dans une dernière étape, l’ensemble des prédicteurs faibles ainsi obtenus sont combinés en pondérant chaque modèle proportionnellement...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations