Gradient Boosting pour les séries temporelles

1. Définition

L’étude et la prédiction des séries temporelles forment un domaine bien identifié du Machine Learning, avec ses approches dédiées.

Une série temporelle se définit comme un ensemble de données, constitué de mesures, nommées échantillons, pour chacune desquelles est connu l’instant précis où la mesure a été réalisée.

Ce peut être par exemple un simple enregistrement sonore, mais aussi un électro-encéphalogramme ou encore un décompte du passage de clients à la caisse d’un magasin.

La valeur enregistrée peut être un simple scalaire, comme lors de la mesure d’une tension en un point précis d’un circuit. Il peut aussi s’agir d’un vecteur, comme c’est le cas d’un électro-encéphalogramme où de nombreux capteurs sont impliqués.

La caractéristique essentielle des séries temporelles est donc cette dépendance au temps, qui est propre aux systèmes en évolution. Ces derniers sont par nature difficilement prédictibles.

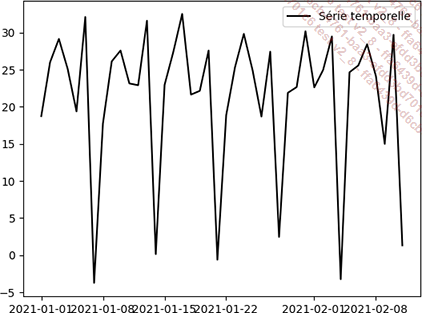
La figure ci-dessous reproduit une série temporelle, où le temps se trouve en abscisse et la valeur échantillonnée en ordonnée :

2. Spécificités

1. Extrapolation et arbres de décision

Un point qui échappe régulièrement aux utilisateurs des méthodes de Gradient Boosting pour les arbres de décision est leur totale incapacité à extrapoler. 

En effet, de par leur nature et en raison de la façon dont ils sont entraînés, les arbres de décision ne peuvent prédire autre chose que ce qu’ils ont déjà rencontré durant la phase d’entraînement.

Le chapitre sur les fondements mathématiques des méthodes de Gradient Boosting a mis en évidence que les prédictions réalisées par un arbre de décision ne font appel qu’à des sommes pondérées. Les poids des feuilles atteintes après parcours de l’arbre sont les seuls éléments à intervenir dans la prédiction, et leurs valeurs sont des combinaisons linéaires des échantillons du dataset d’entraînement.

À aucun moment une des features en entrée n’est multipliée par un quelconque coefficient pour produire la prédiction.

Dans ces conditions, il est tout à fait impossible d’extrapoler, c’est-à-dire de prolonger une tendance...

1. Exemple simple de périodicité

Les quelques lignes de code suivantes génèrent une série temporelle représentative d’un cas réel. En l’occurrence, il s’agit des ventes quotidiennes d’un produit donné, dans un magasin donné :

import matplotlib.pyplot as plt 
import numpy as np 
import pandas as pd 
 
weekly_sales = [20, 25, 30, 25, 20, 30, 0] 
 
X = pd.DataFrame({'date': pd.date_range(start='1/1/2021',  
end='30/12/2021'), 
                  'value': np.array(weekly_sales * 52) +  
np.random.normal(0, 2, 364)}) 

La série est construite sur la base d’un motif de ventes hebdomadaire auquel un bruit gaussien est rajouté, avec une moyenne nulle et un écart-type de 2.

La série est bien stationnaire, car le niveau de vente globale n’évolue pas au court du temps.

La résolution de la série est quotidienne, c’est-à-dire qu’à chaque jour une unique valeur est associée. Cette série s’étend sur 364 jours afin d’être un multiple de 7 jours.

Le tracé de cette série pour les sept premières semaines fait apparaître la périodicité hebdomadaire, avec notamment les ventes nulles systématiquement tous les dimanches :

De manière générale, quand il y a un phénomène périodique comme le met en avant le tracé ci-dessus, il est intéressant de regarder les valeurs pour des instants récurrents...

1. Cloisonnement

Notamment, il faut prendre bien soin de cloisonner de manière parfaitement hermétique la construction des datasets d’entraînement et de validation/test utilisés dans les phases de cross-validation.

En effet, il est impératif de construire toutes les features de manière indépendante sur ces deux types de datasets. En aucun cas il ne faut ajouter de features temporelles avant de faire le découpage.

Il faut à l’inverse procéder d’abord au découpage en datasets d’entraînement et de test, puis enrichir ensuite les deux types de datasets.

2. Fuite de données

Si ce cloisonnement n’était pas scrupuleusement respecté, le modèle se retrouverait dans sa phase d’entraînement face à un problème de fuite de données. C’est-à-dire que les datasets de test, situés dans le futur, auraient des features calculées en partie avec des données du futur.

Il y aurait alors un biais dans le modèle qui conduirait à un sur-apprentissage. Les performances seraient excellentes lors de l’entraînement...