Introduction à l'analyse de données
Introduction
Maintenant, on maîtrise le langage R, plus précisément ses fondamentaux : la syntaxe, les structures de données et surtout comment importer et nettoyer les données d’une source quelconque dans l’environnement de travail R.
Les données sont disponibles, il est évident que l’étape qui suit concerne les traitements de base notamment la description des données à travers des mesures d’indicateurs statistiques ou des présentations graphiques qui permettent d’avoir une idée sur les caractéristiques des variables présentes dans le jeu de données.
Ainsi, dans ce chapitre, on abordera les outils de base d’analyse des variables d’un jeu de données qu’on importera d’une source de données d’un côté, et d’un autre côté on découvrira les fonctions R permettant de générer des variables aléatoires et simuler des expériences.
Préparation des jeux de données
1. Charger et comprendre les données
Pour aborder les concepts de base de l’analyse de données, on va considérer les données financières suivantes collectées depuis la plateforme Yahoo Finance sur les sociétés cotées de différents secteurs d’activités, qu’on va stocker dans l’objet findata.RData qui se trouve dans le dossier /data :
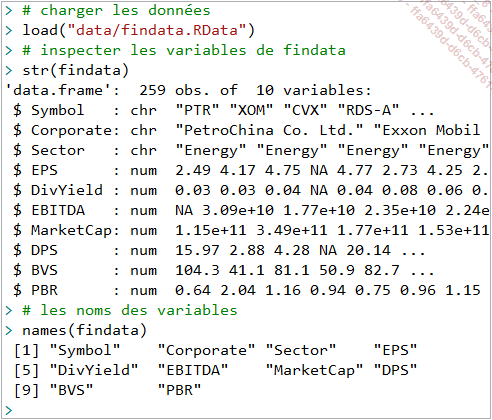
L’objet findata se compose de 259 sociétés décrites par dix variables qui sont heureusement bien encodées dans les classes qui conviennent :
|
Symbol |
Code de référence de la société à la cote |
|
Corporate |
Dénomination de la société |
|
Sector |
Secteur auquel appartient la société |
|
EPS |
Moyenne du résultat net par action |
|
DivYield |
Moyenne du rendement de l’action : dividende/résultat net |
|
EBITDA |
Moyenne du résultat opérationnel avant dépréciations et amortissements |
|
MarketCap |
Moyenne capitalisation : nombre d’action x cours |
|
DPS |
Moyenne dividende par action |
|
BVS |
Moyenne valeur comptable de l’entreprise par action |
|
PBR |
Moyenne multiple du cours sur capitaux à long terme |
On peut avoir un aperçu des données avec les fonctions head() ou tail() :
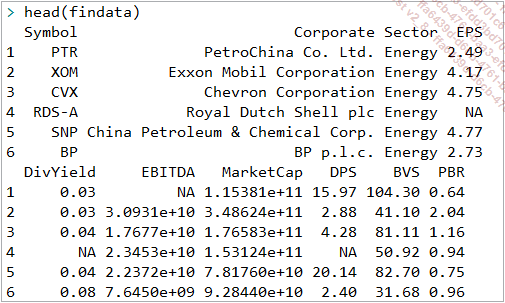
Plus important encore, il est pertinent d’analyser l’existence de données manquantes pour déterminer l’action à entreprendre pour les gérer.
2. La gestion des données manquantes
a. Inspecter l’existence des données manquantes
Le traitement des données manquantes n’est pas à prendre à la légère, il est important de savoir leur part dans le jeu de données pour décider d’une méthode adéquate pour les gérer. Dans le chapitre Importer et exporter des données avec R, notamment, on a vu des fonctions permettant de détecter et de gérer la présence de valeurs ou données manquantes, is.na(), na.omit(), na.exclude(), etc. Mais cette fois, on va découvrir le package mice qui offre des fonctions dédiées à l’exploration des valeurs ou données manquantes :

C’est la fonction md.pattern() qui permet de visualiser le nombre de valeurs manquantes par variable...
Analyse descriptive des variables quantitatives
Dans cette section, il s’agira d’acquérir les fonctions nécessaires à la compréhension par la description et l’association des variables numériques ou non en les considérant individuellement par le calcul de statistiques.
1. Cas univarié
a. Mesures de tendance centrale
En statistique descriptive, les mesures de tendance centrale font référence aux valeurs spéciales ou d’une variable autour desquelles les données ont tendance à se regrouper :
La moyenne
Sans doute l’indicateur statistique le plus utilisé est la moyenne arithmétique :
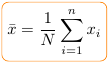
Et s’obtient sous R avec la fonction mean() comme suit :
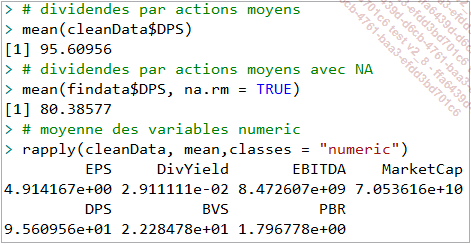
Pour plus de pertinence, on peut calculer des moyennes sur des groupes :
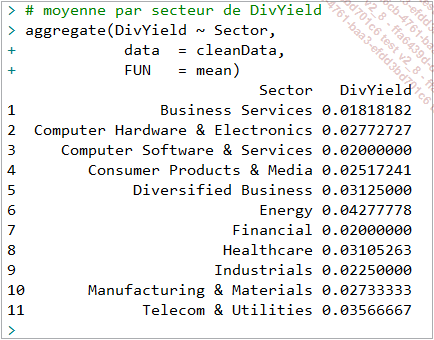
On ne dispose pas que de la moyenne arithmétique, mais également des moyennes géométriques et harmoniques qui sont en fait issues respectivement d’une log-transformation et de l’inverse de la variable initiale. Néanmoins, au besoin, le package psych de R propose les fonctions geometric.mean() et harmonic.mean() pour leur calcul.
Par ailleurs, on n’en a pas encore fini avec la fonction mean(), cette derniere est généralement connue pour son second argument na.rm, cependant, elle dispose d’un argument très important, il s’agit de l’argument trim qui permet de gérer les valeurs aberrantes. Il prend en valeur une proportion ou fraction inférieure à 1/2 dénotant de la proportion des observations à occulter, donc à considérer comme aberrantes ou extrêmes. Car la moyenne est certes un indicateur très pratique et simple à interpréter, mais il souffre de la présence de valeurs aberrantes ou extrêmes.
On considère la variable age contenant les valeurs suivantes :
|
11.5, 11, 3.0, 12, 12.5, 5.0, 10, 12.0, 11, 29, 12.5, 13.5, 30, 28, 12.0 |
Quel devrait être l’âge moyen ?
Naïvement, on peut précéder comme suit :

Mais ce résultat s’écarte de la définition qu’on donne à une caractéristique de tendance centrale qui devrait être représentative. Or, le résultat obtenu ne semble pas traduire ce fait. D’où l’intérêt...
Analyse descriptive des variables catégorielles
Les caractéristiques des variables catégorielles font de ces dernières des cas à part lorsqu’il s’agit de calculer des indicateurs statistiques. Il faut leur donner un bon encodage ordinal ou nominal et les organiser dans des tableaux statistiques de la classe table, facilement traitables par les formules habituelles.
1. Tableaux statistiques pour les variables catégorielles
Pour les besoins des illustrations, on va recourir au jeu de données Film du package Stat2Data, en raison de sa simplicité et aussi parce que ça parle de films ! Ce jeu de données contient dix variables (titre, année de sortie, durée, casting, note, nombre de lignes de la description du film, pays d’origine, etc.) décrivant cent films.
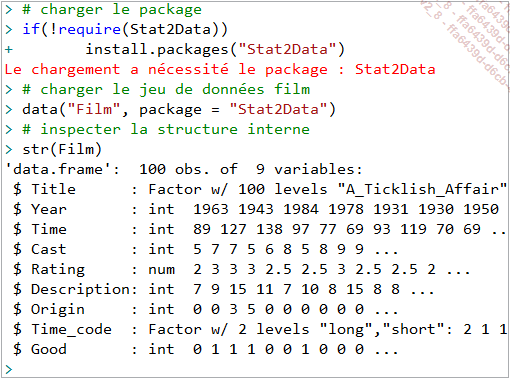
a. Les tableaux de fréquences
Les tableaux de fréquences sont tout simplement des objets de la classe table qui présentent sous forme tabulaire le nombre ou la proportion de chaque niveau ou catégorie d’une variable catégorielle.
Les fonctions table() et prop.table()
Déjà utilisée lorsqu’on étudiait les objets factor, la fonction table() permet de dénombrer les niveaux d’une variable catégorielle :
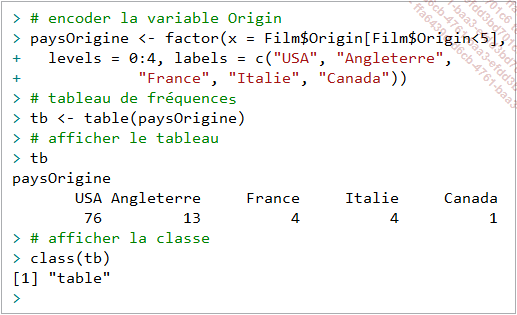
On peut présenter le résultat sous forme verticale en recourant à la fonction as.data.frame() :
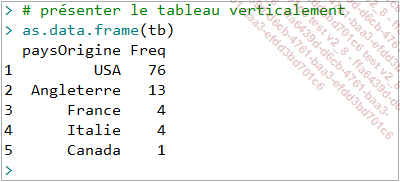
La fonction prop.table() reçoit en argument un objet table, et renvoie en résultat un tableau de fréquence relative ou en proportion :
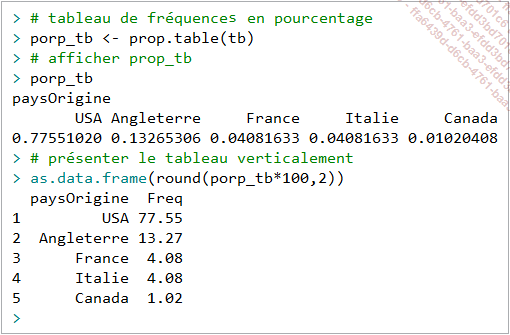
La fonction table() permet également de gérer les valeurs manquantes avec l’argument useNA, qui par défaut exclut les valeurs manquantes :
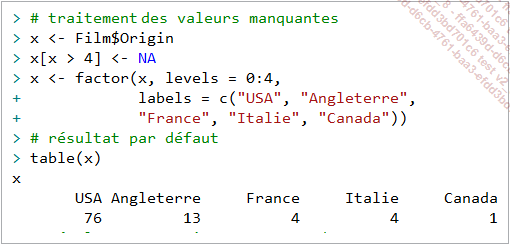
Mais cet argument peut prendre d’autres valeurs additionnelles à savoir "ifany" ou "always" :
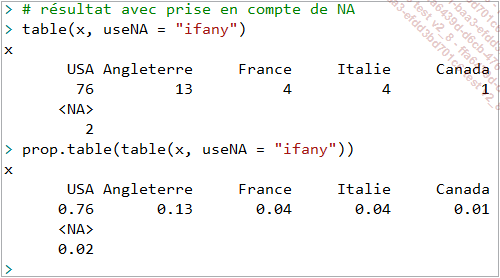
La fonction table() peut être utilisée en conjonction avec la fonction addNA() pour définir le comportement des NA dans le tableau de sortie. addNA() permet d’ajouter les NA comme une catégorie si ce n’est pas le cas dans la variable d’origine :...
Visualisation graphique des données
Laissés pour compte en analyse des données, les graphiques sont primordiaux pour cerner certains aspects d’une variable ou d’un jeu de données en général. Les graphiques permettent notamment :
-
D’inférer sur les hypothèses et orienter le statisticien sur le choix d’un tel ou tel autre modèle.
-
De détecter l’existence d’un schéma ou pattern dans les données, détecter une tendance…
-
De deceller les valeurs extrêmes ou aberrantes.
-
De présenter des concepts complexes (les mesures quantitatives) plus simplement pour les non-initiés.
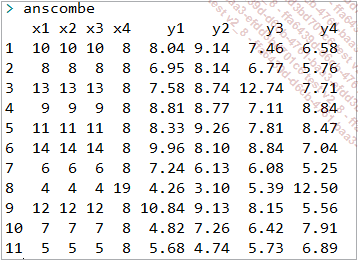
Une illustration typique pour démontrer la nécessité de combiner l’analyse graphique à l’analyse quantitative lors d’une phase exploratoire des données se trouve dans le célèbre jeu de données d’Anscombe :
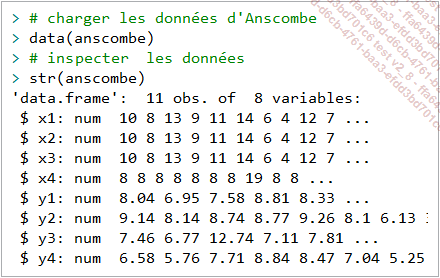
Comme on peut lire dans le code ci-dessus, on a des variables x et y, indicées pour indiquer qu’elles appartiennent en fait à 4 jeux de données (d’où l’appellation quartet) :
Une analyse descriptive avec la fonction summary() montre une similitude entre les variables pour les différentes mesures statistiques ci-après.
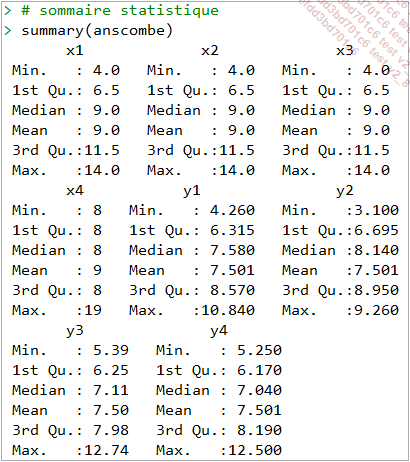
Ainsi, on pourrait par exemple inférer sur la base de ces résultats une possible appartenance des quatre échantillons à une même population.
Toutefois, une analyse graphique des mêmes jeux données présentée par la figure ci-dessous apporte un éclairage sur les différences existant dans ces jeux de données :

En résultat du code ci-dessus, on obtient en réalité des jeux de données montrant des schémas différents, suivant ou non une tendance.
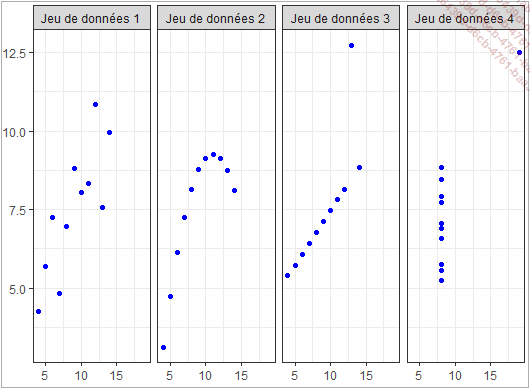
L’idée que véhicule le Quartet d’Anscombe, c’est que la visualisation graphique n’est pas une option en analyse de données, elle doit toujours accompagner une analyse quantitative.
Toutefois, si on recourt à des mesures de forme de la distribution on pourrait aboutir au même résultat qu’avec les graphiques. Par ailleurs, il faut noter quand même que l’analyse graphique est limitée, notamment lorsqu’on est en analyse multivariée...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations



