Modèles statistiques classiques
Introduction
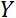 d’intérêt à travers
une fonction qui s’exprime et implique très souvent d’autres
variables aléatoires
d’intérêt à travers
une fonction qui s’exprime et implique très souvent d’autres
variables aléatoires 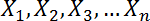 . La première, la variable Y est souvent
dénommée variable de réponse, variable à expliquer
ou variable dépendante ou encore variable à prédire,
alors que les autres variables
. La première, la variable Y est souvent
dénommée variable de réponse, variable à expliquer
ou variable dépendante ou encore variable à prédire,
alors que les autres variables 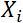 sont dénommées variables explicatives, prédictives
ou encore variables indépendantes. On distingue notamment
:
sont dénommées variables explicatives, prédictives
ou encore variables indépendantes. On distingue notamment
:|
Modèles |
Variable de réponse |
Variable explicative |
|
Régression linéaire simple |
1 variable continue |
1 variable continue |
|
ANCOVA |
1 ou plusieurs variables qualitatives et continues |
|
|
Régression linéaire multiple |
||
|
ANOVA |
1 ou plusieurs variables qualitatives ou facteurs |
|
|
MANOVA |
Plusieurs variables continues |
|
|
Analyse discriminante |
1 variable catégorielle spécifiquement dichotomique |
1 ou plusieurs variables qualitatives et continues |
|
Régression logistique |
Analyse de la variance (ANOVA)
Dans le précédent chapitre, on a abordé plusieurs tests, dont notamment le test de comparaison de moyennes d’un - cas de comparaison par rapport à une référence, c’est pour ça que l’on parle de test de conformité - ou deux échantillons de données. L’ensemble de ces tests est souvent dénommé T-Test à cause de la loi T de Student que suit la distribution sous-jacente de l’échantillon.
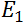 à celle de
à celle de 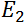 , de
, de 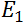 à celle
de
à celle
de 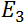 et finalement de
et finalement de 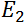 à
à 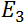 . Ça pourrait fonctionner si ça
n’impliquait pas un risque d’erreur de Type I plus important (voir
dans le précédent chapitre pour la définition).
En effet, si l’on fixe ce risque pour chaque T-Test à 5 % comme
on a l’habitude de faire, pour la comparaison combinée
des trois T-Test, en supposant les échantillons indépendants,
on se retrouve avec un risque d’erreur de Type I égal à
. Ça pourrait fonctionner si ça
n’impliquait pas un risque d’erreur de Type I plus important (voir
dans le précédent chapitre pour la définition).
En effet, si l’on fixe ce risque pour chaque T-Test à 5 % comme
on a l’habitude de faire, pour la comparaison combinée
des trois T-Test, en supposant les échantillons indépendants,
on se retrouve avec un risque d’erreur de Type I égal à 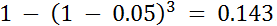 , ce qui est évidemment trop élevé pour
un risque d’erreur de Type I surtout si on a un nombre K élevé de
moyennes.
, ce qui est évidemment trop élevé pour
un risque d’erreur de Type I surtout si on a un nombre K élevé de
moyennes.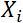 qualitatives (par exemple, un traitement médical,
emplacement des magasins de ventes, etc.), en l’occurrence dénommées
facteurs, dont les différentes modalités ou niveaux
représentent des groupes qui s’apparentent donc aux échantillons dont...
qualitatives (par exemple, un traitement médical,
emplacement des magasins de ventes, etc.), en l’occurrence dénommées
facteurs, dont les différentes modalités ou niveaux
représentent des groupes qui s’apparentent donc aux échantillons dont...Modèles de régression linéaire
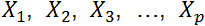 . Concrètement,
on suppose qu’il existe une relation entre Y une variable continue
et X = (
. Concrètement,
on suppose qu’il existe une relation entre Y une variable continue
et X = (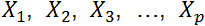 ) qui se formalise
de manière générale comme suit :
) qui se formalise
de manière générale comme suit :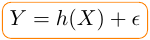
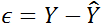 , le terme
d’erreur ou résidu qui est une variable aléatoire
totalement indépendante de X qui suit une loi normale
, le terme
d’erreur ou résidu qui est une variable aléatoire
totalement indépendante de X qui suit une loi normale 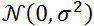 et :
et :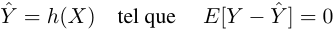
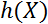 , appelée fonction hypothèse
(puisqu’on ne la connaît pas, elle juste supposée),
capture l’information systémique de Y connaissant X ce
qui se traduit par l’égalité suivante :
, appelée fonction hypothèse
(puisqu’on ne la connaît pas, elle juste supposée),
capture l’information systémique de Y connaissant X ce
qui se traduit par l’égalité suivante :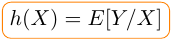
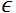 . Ainsi, on comprend que pour que
. Ainsi, on comprend que pour que 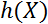 soit la plus représentative possible
de
soit la plus représentative possible
de 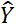 (la prévision de
Y), il faudrait que
(la prévision de
Y), il faudrait que 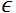 soit minimale.
soit minimale.Dans cette section, la régression linéaire sera abordée sous plusieurs aspects à travers des applications R.
1. Régression linéaire simple
a. Formalisation et estimation
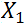 ) et la fonction
hypothèse à la forme suivante :
) et la fonction
hypothèse à la forme suivante :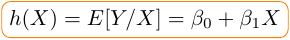
Donc, la relation entre Y et X pourra se formuler comme suit :
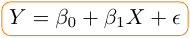
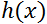 est en fait l’équation d’une droite
dont
est en fait l’équation d’une droite
dont 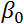 est l’ordonnée à l’origine
ou intercept en anglais, et
est l’ordonnée à l’origine
ou intercept en anglais, et 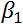 est le coefficient
directeur ou slope en anglais. Il faut donc déterminer les paramètres
est le coefficient
directeur ou slope en anglais. Il faut donc déterminer les paramètres 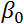 et
et 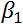 qui peuvent être
estimés au moyen de la méthode des moindres carrés
ordinaires ou Ordinary Least Square ou OLS method (en anglais).
qui peuvent être
estimés au moyen de la méthode des moindres carrés
ordinaires ou Ordinary Least Square ou OLS method (en anglais). Selon cette méthode, trouver ces paramètres revient à minimiser la somme des carrés des résidus ou Sum of Square Error (SSE) :
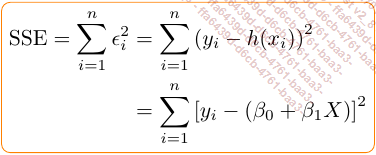
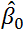 et
et 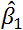 des paramètres
des paramètres 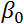 et
et 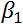 qui rendent
minimale SSE s’obtiennent comme suit :
qui rendent
minimale SSE s’obtiennent comme suit :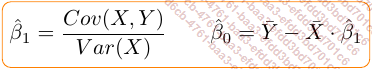
Ces estimateurs sont sans biais compte tenu du théorème GAUSS - MARKOV. Ainsi, sans trop...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations



