Classifieurs linéaires
Objectifs du chapitre
Dans ce chapitre, nous allons explorer les fondements des classifieurs linéaires, une des briques de base du traitement d’images et des réseaux de neurones profonds.
Tout d’abord, nous commencerons par examiner les composantes principales de ces classifieurs. Nous décrirons deux interprétations de leur fonctionnement qui nous permettront d’identifier leurs limites.
Ensuite, nous détaillerons les différentes étapes de leur entraînement, ainsi que les fonctions-coût et les métriques associées.
Ces éléments sont communs à la plupart des applications d’apprentissage automatique, dont les réseaux de neurones. Ils sont cependant plus simples à comprendre dans le contexte des classifieurs linéaires ; ce chapitre nous permet donc d’introduire en douceur certains des principes clefs de l’apprentissage profond.
Pour certaines de ces étapes, nous mentionnerons également le code Keras permettant de les implémenter.
Enfin, nous ferons le lien avec les réseaux de neurones profonds, qui peuvent être vus comme une extension des classifieurs linéaires.
Vocabulaire et notations
1. Étiquettes
Une étiquette (label en anglais) est le véritable objet de la prédiction. Elle est souvent notée y.
Par exemple, pour un problème de prédiction du prix des logements, l’étiquette de chaque logement est son prix de vente.
Pour un problème de classification d’images entre des chiens et des chats, l’étiquette de chaque image est « chien » ou « chat ».
Pour entraîner un modèle, il est nécessaire que toutes les étiquettes aient une représentation numérique. Pour la classification, les étiquettes peuvent être représentées de deux manières différentes :
-
Comme un entier entre 0 et nombre de classes - 1 : par exemple chat = 0, chien = 1.
-
Comme un vecteur, en utilisant l’encodage « un parmi n » (appelé one hot encoding en anglais). Dans ce dernier cas, y est un vecteur de taille nombre de classes. Dans ce vecteur, un seul élément a la valeur 1, et tous les autres ont la valeur 0 : par exemple chat = (1, 0), chien = (0,1).
Dans ce dernier cas, nous noterons yc chacun des éléments de y, l’indice c représentant une classe :
|
y = (yc)c=1…C |
2. Caractéristiques
Les caractéristiques sont des variables d’entrée...
Modèle paramétrique du classifieur linéaire
1. Définition du modèle
Un classifieur linéaire est une fonction affine qui, appliquée aux caractéristiques d’un exemple, renvoie une prédiction en sortie.
Un tel classifieur peut être décrit par deux éléments : une matrice de poids W, qui représente la partie linéaire du modèle, et un vecteur b, appelé vecteur de biais.
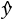 la prédiction du
modèle, il est possible d’écrire :
la prédiction du
modèle, il est possible d’écrire :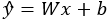
Bien que le modèle mathématique sous-jacent utilisé par un classifieur linéaire soit affine, le terme « linéaire » est tout de même utilisé car ce modèle détermine une frontière de décision linéaire dans l’espace des caractéristiques, comme nous le verrons dans la section Interprétation d’un classifieur linéaire comme un ensemble de plans de séparation de ce chapitre.
Pour illustrer le fonctionnement de ce modèle, prenons l’exemple d’une image de taille 2x2, à classifier en « chat » ou « chien » à l’aide d’un classifieur linéaire.
Le vecteur x correspond à l’ensemble des pixels de l’image...
Étapes de l’entraînement
Entraîner un classifieur linéaire (c’est-à-dire estimer les paramètres optimaux du classifieur pour une application donnée) se fait en plusieurs étapes.
Tout d’abord, il est nécessaire de séparer l’ensemble de données en plusieurs sous-ensembles : les données d’entraînement, les données de validation, et les données de test.
Nous pouvons ensuite réaliser l’optimisation afin d’identifier les meilleurs paramètres.
Enfin, nous calculons diverses métriques pour évaluer la performance du modèle.
Nous allons maintenant détailler chacune de ces étapes une à une.
Séparation des données
1. Principe
Lorsqu’on entraîne un modèle d’apprentissage automatique, une des problématiques principales est la suivante : comment s’assurer que les performances obtenues sur un jeu de données se généralisent à un autre ?
C’est à cette problématique que répond la séparation des données.
L’ensemble d’entraînement est celui sur lequel l’optimisation des paramètres est effectuée.
L’ensemble de validation est utilisé pendant l’entraînement : à chaque itération de l’entraînement, nous calculons diverses métriques sur cet ensemble. Ces métriques sont utilisées pour sélectionner divers hyperparamètres du modèle et de l’apprentissage. Les hyperparamètres sont des variables influençant le comportement global du modèle, qui doivent être choisies avant le début du processus d’apprentissage. Contrairement aux paramètres internes, qui sont appris à partir des données pendant le processus d’entraînement, les hyperparamètres sont définis par l’utilisateur.
La sélection des hyperparamètres sera décrite plus en détail dans la section Sélection des hyper-paramètres du chapitre Réseaux de neurones profonds.
L’ensemble de tests n’est utilisé qu’à la toute fin, afin d’estimer les performances du modèle sur un ensemble jamais vu.
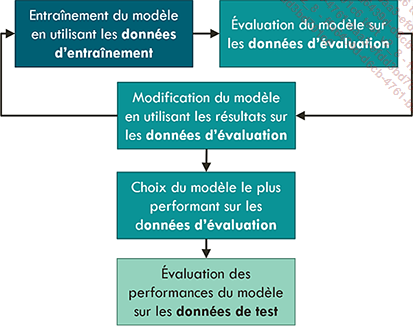
Utilisation des données d’entraînement, validation et test
Si le modèle est très simple, et qu’il n’est pas prévu d’utiliser des métriques pour sélectionner des hyperparamètres ou interrompre l’optimisation au cours de l’entraînement, alors il est possible de ne pas utiliser d’ensemble de données de validation, et de séparer le jeu de données en seulement deux sous-ensembles : entraînement et test.
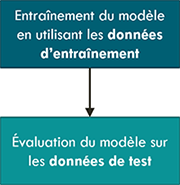
Utilisation des données d’entraînement et de test
Prenez garde : si les performances sur l’ensemble de tests sont décevantes, et que des paramètres sont modifiés de manière répétée...
Optimisation des paramètres
1. Fonction-coût
Trouver les paramètres optimaux se fait par un processus itératif : à partir d’une valeur initiale choisie aléatoirement, ils sont ensuite modifiés de manière à réduire l’erreur entre les prédictions réalisées par le modèle avec les paramètres actuels et les vraies prédictions.
Pour cela, il est nécessaire de disposer d’une manière de calculer cette erreur. C’est la fonction-coût du réseau (appelée cost function ou loss en anglais).
Chaque type de problème nécessite une fonction de perte différente. Nous ne parlerons ici que de classification, et nous introduirons dans les chapitres Détection et Segmentation les fonctions de perte utilisées pour les autres applications telles que la détection.
Une bonne fonction-coût doit remplir les trois critères suivants :
-
Elle représente la performance du modèle : plus sa valeur est faible, plus le modèle est performant.
-
Elle est suffisamment régulière pour pouvoir être optimisée facilement.
-
Son calcul est suffisamment rapide pour ne pas ralentir le processus d’optimisation.
En classification, c’est généralement l’erreur quadratique moyenne et l’entropie croisée qui sont utilisées.
a. Erreur quadratique moyenne
L’erreur quadratique moyenne (Mean Squared Error ou MSE en anglais) mesure la moyenne du carré de l’écart entre les prédictions du classifieur linéaire et les étiquettes réelles.
Pour illustrer son calcul, imaginons que l’on ait un classifieur à trois classes (chats, chiens et grenouilles), ainsi que deux images d’entraînement, que nous allons utiliser pour calculer la fonction-coût.
La première image représente un chat, et a obtenu les scores suivants : (5, 3, -1). Elle est donc correctement classifiée comme un chat.
La seconde image, qui représente une grenouille, a obtenu les scores suivants : (2, 3, -3). Elle est donc incorrectement classifiée comme un chien.

Score obtenu pour chacune des classes d’intérêt, pour deux images d’entraînement
Pour...
Métriques permettant d’évaluer un modèle de classification
Les métriques sont des mesures de la performance d’un modèle. En ce sens, elles sont proches des fonctions-coût. Contrairement à ces dernières, elles n’ont cependant pas besoin d’être différentiables ni rapides à calculer. Pour cette raison, il est courant d’utiliser plusieurs métriques différentes en classification.
Comme nous l’avons mentionné dans la partie sur la séparation des données, pour estimer la performance d’un modèle sur de nouvelles données, il est capital de calculer les métriques sur des données qui n’ont pas été utilisées pour l’entraînement. Utiliser ces dernières vous donnera une idée surestimée des performances. Il est capital de calculer ces mesures sur l’ensemble de données de test.
1. Classification binaire
Commençons par décrire les métriques utilisées en classification binaire. Les métriques utilisées en classification multiclasse en découlent.
a. Matrice de confusion
La matrice de confusion (ou confusion matrix en anglais) est un tableau à double entrée répertoriant le nombre d’exemples de chaque classe ayant été classifiés comme chacune des classes d’intérêt.
Pour une classification binaire, ce tableau possède deux lignes et deux colonnes.
Prenons l’exemple d’un classifieur de chiens et de chats.
La première ligne représente le nombre d’images de chats. Dans la première colonne est répertorié le nombre de ces images ayant été effectivement classifiées comme des chats. Ces images sont appelées vrais positifs.
En classification binaire, nous considérons généralement que nous avons une classe « positive » et une classe « négative ». Évidemment, il est possible de choisir n’importe laquelle des deux classes comme classe « positive », et ce choix n’a aucun impact, ni sur l’entraînement ni sur le calcul des métriques. Dans cet exemple, nous considérons que la classe « chat »...
De l’apprentissage automatique aux réseaux de neurones
1. Sélection automatique des caractéristiques
Dans les exemples présentés au cours de ce chapitre, nous avons directement alimenté le classifieur linéaire avec les intensités de l’image en entrée. Cependant, cette approche n’est pas recommandée en pratique en raison de la grande dimensionnalité des images, qui entraîne un grand nombre de paramètres à estimer.
En pratique, c’est une approche en deux étapes qui est appliquée pour entraîner un classifieur linéaire. Tout d’abord, nous calculons certaines caractéristiques des images, et nous les concaténions en vecteurs de caractéristiques. Ce sont ces derniers qui sont donnés en entrée au classifieur.
Pendant l’entraînement, seuls les poids du classifieur linéaire sont mis à jour, l’extracteur de caractéristiques restant inchangé.

Application du classifieur linéaire aux images directement (en haut), et aux caractéristiques issues des images (en bas)
Il existe plusieurs avantages à utiliser des caractéristiques plutôt que les images en entrée :
-
Ceci permet de réduire la dimension du vecteur x. En effet, les caractéristiques choisies ont une dimension inférieure à celle...
Exemple pratique : entraîner un classifieur linéaire à distinguer les chats des chiens
Nous pouvons maintenant regrouper toutes ces étapes pour entraîner un classifieur linéaire à distinguer des photographies de chats de photographies de chiens.
Les images que nous allons utiliser sont issues d’une compétition de la plateforme Kaggle. Cette compétition, datant de 2013, a été remportée par un Français, Pierre Sermanet (qui travaille pour Google Brain au moment de l’écriture de cet ouvrage), qui a obtenu une précision de 98,9 % en utilisant un réseau de neurones convolutionnel.
La précision attendue avec un classifieur linéaire est beaucoup plus faible.
Le code pour cet exemple se trouve dans le notebook intitulé « classifieur_lineaire.ipynb ».
Conclusion
Dans ce chapitre, nous avons décrit le fonctionnement des classifieurs linéaires.
Nous avons également détaillé le processus d’entraînement et de validation d’un modèle d’apprentissage automatique : la séparation des données, les différentes fonctions-coût et métriques de la classification, et l’optimisation par descente de gradient stochastique sont des concepts de base qui sont également utilisés en apprentissage profond.
Nous avons également examiné les avantages et les limites des classifieurs linéaires, et décrit en quoi ces derniers constituent une première étape cruciale dans la construction de réseaux de neurones profonds plus complexes et plus puissants.
Dans le prochain chapitre, nous utiliserons ces concepts pour décrire les réseaux de neurones profonds et la manière dont ils sont entraînés.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations



