Les variables et opérateurs

1. Principe

Vous savez grâce au chapitre précédent comment l’ordinateur se représente les chiffres et les nombres : sous forme binaire. De même la mémoire de l’ordinateur, composée de cases, peut contenir des informations, notamment ces fameux nombres. En programmation, il faut quelque chose de simple, pratique et souple à manipuler pour représenter ces nombres.

Chaque case de la mémoire est numérotée. Si la mémoire fait, disons, 256 octets, et que chaque case peut contenir un octet, alors il y a 256 cases numérotées de 0 à 255. On peut donc obtenir la valeur d’une case depuis son numéro, en disant que la case 74 contient la valeur 212. Là où ça se complique, c’est que la mémoire de vos ordinateurs atteint un nombre très important de cases. Avec 1 Go de mémoire, vous avez 1073741824 cases pouvant contenir chacune un octet. Comment voulez-vous vous souvenir de chaque numéro de case ? C’est bien entendu impossible.

Si par contre vous donnez un nom ou une étiquette à chaque valeur contenue dans la case, ou à une suite de valeurs de plusieurs cases, pour vous en rappeler plus facilement, cela devient bien plus évident. C’est ce qu’on appelle une variable. En informatique, une variable est l’association d’une étiquette à une valeur. Vous nommez la valeur. La variable représente la valeur et se substitue à elle. La variable est donc la valeur. Mais comme son nom l’indique, cette valeur peut changer dans le temps, soit que la variable ne représente plus la (ou les) même(s) case(s) mémoire, soit que la valeur de la case a changé.

Quel nom donner à une valeur ? Le nom que vous voulez et qui, si possible, est en rapport avec ce que représente la valeur. Ce peut être une lettre, une association de lettres et de chiffres, ou d’autres symboles. Le formalisme des noms des variables dépend du langage utilisé. Parfois, un caractère spécifique indique le type (que vous rencontrerez...

1. Les affectations

Le symbole d’affectation "←" fait partie d’une grande famille, celle des opérateurs. Comme son nom l’indique, un opérateur est utilisé pour et dans des opérations. Le symbole "←" est un opérateur d’affectation. Il existe plusieurs opérateurs qui servent aux calculs, affectations, comparaisons, rotations (de bits), groupages, etc.

2. Les opérateurs arithmétiques

Pour que les algorithmes puissent effectuer des calculs, il faut pouvoir au moins faire des opérations simples. Vous utiliserez pour cela les symboles suivants :

Ces opérateurs sont dits binaires car ils s’utilisent avec deux valeurs : une avant le symbole et une après. Les valeurs avant et après peuvent être des données (de même type que la variable qui reçoit les résultats) ou des variables. Voici un exemple d’opérations dans un simple algorithme qui calcule la surface et le périmètre d’un cercle.

PROGRAMME CERCLE 
VAR 
  r, PI, surface,perimetre:réels 
DEBUT 
  PI←3,1415927 
  r←5,2 
  surface←PI * r * r 
  perimetre←2 * PI * r 
  Afficher surface,perimetre 
FIN
 

Ici il n’y a que des multiplications. Vous pouvez déjà remarquer que vous avez parfaitement le droit de chaîner vos calculs et de mélanger les données et les variables. Simulez les deux calculs :

surface←PI * r * r 
surface←3,1415927 * 5,2 * 5,2 
surface←84.948666608 
 
perimetre←2 * PI * r 
perimetre←2 * 3,1415927 * 5,2 
perimetre←32.67256408
 

En C# :

class chap2_cercle {  
  public static void main(String[] args) {  
    double pi,r,surface,perimetre;  
    pi=3.1415927;  
    r=5.2;  
  ...

1. Les nombres négatifs

Un nombre signé, par exemple sur 8 bits, contient un bit réservé pour le signe. C’est en tout cas ainsi qu’on vous le présente pour plus de compréhension. Généralement c’est le bit de poids fort, le plus à gauche, qui sert pour le signe : à 0 le nombre est positif, à 1 il est négatif. Par exemple -9₍₁₀₎ devrait être représenté par 10001001₍₂₎. Cette représentation pratique pour le lecteur ne l’est cependant absolument pas pour l’ordinateur.

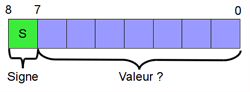
Le bit de poids fort représente le signe

Additionnez -9 et 30, vous obtenez 21.

En binaire, 30 équivaut à 00011110. Le binaire s’additionne comme le décimal : 1+1=10 donc retenue de 1, et ainsi de suite :

 00011110 (30) 
+10001001 (-9) 
=10100111 (-39)
 

Il y a un problème ! Vous devriez obtenir 21 soit 00010101 ! C’est qu’en réalité un nombre négatif n’est pas représenté comme ceci. L’ordinateur "ruse" avec les manipulations binaires. L’astuce consiste à prendre le complément à un de la valeur binaire en valeur absolue (-9 => 9), et de lui rajouter 1. On obtient au final un complément à deux. Le complément à un consiste à remplacer tous les zéros (0) par des un (1) et tous les 1 par des 0. Le complément à deux consiste à ajouter 1 au complément à un.

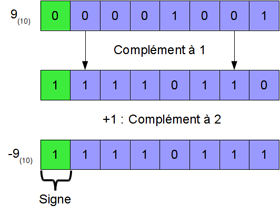
Les nombres négatifs en complément à deux

Pour convertir un nombre décimal négatif en binaire, il faut donc suivre les étapes suivantes :

1. Convertir le nombre décimal positif (valeur absolue) en binaire.

2. Complémenter à 2 le nombre binaire obtenu.

Pour convertir un nombre binaire négatif en décimal, on fait l’inverse :

1. Complémenter à 2 le nombre binaire.

2. Convertir le nombre binaire obtenu en décimal, et rajouter le signe.

Maintenant, additionnez ce résultat à 30 :

 11110111 (équivaut à -9 représentation machine) 
+00011110 (30) 
=00010101 (21 - plus une retenue)
 

Vous obtenez le bon résultat !...

1. Langages typés ou non

Quelques langages sont très souples avec les variables. Vous pouvez tout d’abord y mettre des nombres, puis du texte, puis de nouveau des nombres. Ces langages sont dits "non typés". Certains poussent le raisonnement assez loin : une variable peut contenir le chiffre 3, et l’autre le texte "3 petits cochons", il pourra les additionner (ce qui devrait donner 6) ! C’est le cas du PHP par exemple : le type de la variable dépend alors de son contexte d’utilisation, le langage tentant de convertir son contenu quand c’est possible.

À l’inverse, d’autres langages sont de "typage fort" où toutes les variables doivent être déclarées de manière extrêmement précise : type, signe, longueur, et les éventuelles conversions doivent être explicites.

En algorithmique, vous vous contenterez de donner le nom, le type et éventuellement la taille de la variable, qui gardera ses propriétés tout au long de l’algorithme, sa valeur pouvant bien entendu évoluer.

2. La gestion de la mémoire

La gestion de la mémoire est le calvaire des programmeurs en langages de bas niveau ou même de haut niveau quand ceux-ci laissent cette tâche au programmeur. C’est le cas de langages comme le C ou le C++. Imaginez une chaîne de caractères...