Conditions, tests et booléens

1. Les conditions sont primordiales

Dans notre vie, notre comportement est dirigé par une multitude de décisions à prendre. Toujours avec l’exemple du passage piéton, nous allons traverser si le voyant piéton est vert, sinon nous allons attendre s’il est rouge. Il en va de même pour un algorithme et un programme, nous devons guider l’ordinateur pour qu’il puisse prendre les bonnes décisions et donc exécuter correctement nos instructions.

Souvenez-vous que nous devons tout expliquer à la machine, elle ne prendra jamais une décision par elle-même, sauf peut-être le fait de s’éteindre en cas de court-circuit. Vous devez indiquer à l’ordinateur dans quels cas il peut exécuter vos instructions. Par exemple comme quand un adulte apprend à un jeune enfant à dessiner : l’adulte lui montre comment tenir le crayon, quel est le bout qui permet de dessiner, qu’on ne peut dessiner que sur une feuille et non sur une table ou un mur, etc. L’avantage de la programmation pour nous est que nos explications sont beaucoup plus simples à formuler et que la machine nous écoute forcément sans jamais en faire à sa tête et surtout comprend parfaitement du premier coup.

Les tests et conditions représentent une idée de base très simple pour bien guider notre programme : choisir d’exécuter telle ou telle instruction selon la validité d’une condition. Nous testons donc la validité d’une condition pour donner l’autorisation ou non de continuer le déroulement du programme comme : si le feu piéton est vert (condition), alors je traverse (instruction).

Le test peut également contenir une ou plusieurs alternatives : si le feu piéton est vert (condition), alors je traverse (instruction) sinon j’attends que le feu piéton passe au vert.

Qui dit condition, dit booléen. Les booléens sont les types les plus simples en informatique. Ils ne peuvent prendre que deux valeurs : VRAI ou FAUX. La relation entre une condition et un booléen est donc totalement explicite car une condition est toujours une expression de type booléenne.

Une condition est systématiquement le résultat d’une comparaison...

1. Conditions multiples

Écrire une condition qui teste la validité d’un seul fait est assez logique, voire simple. Les conditions augmentent en complexité dès lors que nous augmentons le nombre de fais à valider, que ce soit dans la vie de tous les jours ou en informatique.

Lorsque nous testons des conditions multiples en tant qu’être humain, notre cerveau raisonne tellement vite que nous n’avons pas l’impression de réfléchir ni même de résoudre une équation. Et pourtant…

Reprenons l’exemple du passage piéton. Il vous paraît normal, avant de traverser à un feu, de vérifier que le voyant piéton est vert et d’également vérifier qu’aucune voiture ne grille le feu. Vous analysez donc deux conditions et avez l’impression de les faire en même temps avec une seule et unique condition. Mais votre cerveau reçoit bien deux conditions à vérifier, donc il résout ces deux conditions dans une équation.

Comme nous l’avons indiqué dans le chapitre d’introduction de cet ouvrage, vous devez tout décrire à la machine, faire du vrai pas-à-pas, aucun raccourci n’est possible. Il nous faut donc une manière simple de représenter les conditions multiples.

Pour formuler correctement cette équation avec plusieurs conditions, George Boole, un mathématicien du XIX^e siècle, créa une algèbre binaire que Claude Shannon utilisa plus d’un siècle plus tard en informatique. L’algèbre de Boole, appelée aussi logique booléenne selon le contexte, permet d’analyser plusieurs conditions en même temps dans une même équation, donc dans une même structure conditionnelle. Vous comprenez maintenant d’où vient le nom du type booléen.

L’implémentation de cette algèbre est quasiment naturelle en informatique. Un ordinateur fonctionnant par impulsion électrique, le FAUX est donc représenté par le 0 ou l’absence de courant, le VRAI par le 1 ou la présence d’un courant. 

Ce procédé de calcul donne priorité à certaines conditions par rapport à d’autres en fonction des opérateurs...

1. L’importance de l’indentation

Python est un langage d’une syntaxe assez particulière qui nécessite de la rigueur de la part du développeur. Cette rigueur permet d’alléger la syntaxe de Python et de forcer les bonnes pratiques de développement.

En effet, en Python, un code qui n’est pas indenté n’est pas exécutable par l’interpréteur. 

Un script Python est décomposé en blocs. Chaque bloc doit être indenté par une nouvelle tabulation comme le montre la figure ci-dessous. Pour remonter au bloc précédent, il suffit d’enlever une tabulation aux instructions. Pour indiquer à l’interpréteur qu’un bloc commence, l’instruction doit finir par le caractère ":".

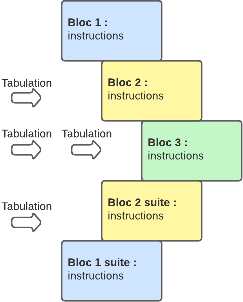
Indentation avec Python

La règle est simple : un bloc d’instructions = une indentation.

Pourquoi abordons-nous cette règle ? Tout simplement car une structure conditionnelle en Python doit être représentée par un bloc. Comme Python utilise le saut de ligne pour la fin d’une instruction, il utilise un bloc pour une instruction conditionnelle.

2. Visibilité des variables

Cette notion de bloc impose d’aborder la visibilité des variables, appelée encore la portée ou le scope.

Les variables d’un algorithme peuvent être utilisées dans n’importe quelle ligne car elles sont toutes connues de tout l’algorithme grâce à leur déclaration dans le bloc VAR avec le début de l’algorithme. Ces variables sont dites globales.

Les variables peuvent être déclarées n’importe quand en Python, contrairement à l’algorithmie. Les variables ne sont donc pas globales mais locales au bloc dans lequel est sont déclarés. Une variable déclarée dans le bloc...