Programmation scientifique
Calcul scientifique
1. Présentation
Le calcul scientifique est un domaine très particulier de l’informatique qui a ses propres exigences et nécessite des besoins très pointus. Il n’est pas pour autant uniquement destiné à des mathématiciens : http://fr.wikipedia.org/wiki/Nombre_premier_de_Mersenne
Le calcul scientifique touche des domaines aussi larges que l’ensemble des filières scientifiques (séquençage ADN, etc.), l’analyse d’image, la cartographie, l’analyse de son ou de vidéos, les mathématiques financières, le pilotage de robots, la génération de graphes, l’animation vidéo, l’analyse linguistique, la lecture de texte par un automate… qui sont tous des domaines de niche. En fait, les mathématiques sont partout et le calcul scientifique également.
N’importe quel projet informatique peut y avoir recours, y compris un projet qui n’aurait a priori rien à voir avec le domaine de la science, tel qu’un projet de gestion documentaire. En effet, les systèmes de classement et les fonctions de recherche de documents peuvent utiliser du calcul scientifique.
On peut également citer l’exemple de la retouche d’image ou du floutage vidéo en temps réel, qui sont des domaines d’application du calcul scientifique auxquels on ne pense...
Tableaux multidimensionnels
1. Création
Un tableau NumPy peut être créé à partir d’une liste Python :
>>> a = array([2, 3, 4]) Attention : il ne faut pas confondre ce tableau à celui du module array.
Lorsque l’on affiche ce tableau, il se présente d’ailleurs sous la forme d’une liste :
>>> print(a)
[2, 3, 4] Mais on peut visualiser le type des éléments qu’il contient :
>>> a.dtype
dtype('int64') Ce résultat peut changer en fonction de votre plateforme (et du compilateur C qui se trouve derrière votre Python), mais vous aurez un type entier. Si un seul nombre n’est pas entier, vous aurez un type réel :
>>> b = array([1.2, 3.5, 5.1])
>>> b.dtype
dtype('float64') On peut aussi créer très rapidement des tableaux de plusieurs dimensions à partir de listes de listes ou de listes de n-uplets :
>>> array( [ (1.5,2,3), (4,5,6) ] )
array([[ 1.5, 2. , 3. ],
[ 4. , 5. , 6. ]])
>>> array( [ ((1.5,2,3), (4,5,6)), ((1.5,2,3), (4,5,6)) ] )
array([[[ 1.5, 2. , 3. ],
[ 4. , 5. , 6. ]],
[[ 1.5, 2. , 3. ],
[ 4. , 5. , 6. ]]]) Lors de l’affichage, la seconde dimension apparaît grâce au saut de ligne, la troisième grâce à deux sauts, ce qui laisse apparaître une ligne blanche.
Comme l’outil est très souple, on peut aussi tout simplement générer une liste à l’aide d’un générateur, similaire à range :
>>> arange(15)
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]) Il peut également prendre un pas :
>>> arange( 10, 30, 5 )
array([10, 15, 20, 25]) Mais peut aussi fonctionner avec des nombres réels :
>>> arange( 0, 2, 0.3 )
array([ 0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8]) Enfin, une fois que l’on a généré une liste de nombres, on peut la remodeler à volonté, nous permettant...
Matrices
Si les tableaux sont des objets malléables représentant un ensemble de données quelconque, les matrices sont des objets mathématiques aux règles strictes.
Il y a cependant quelques similarités entre les matrices et les tableaux. Toujours est-il que NumPy permet de les manipuler très simplement.
Voici comment créer une matrice, à partir d’une simple chaîne de caractères :
>>> A = matrix('1.0 2.0; 3.0 4.0') Notez que l’espace sert à séparer les éléments d’une même ligne et que le point-virgule sert à séparer les lignes entre elles.
Lorsque l’on affiche une matrice, cela se présente toujours sous la forme d’une liste de listes, mais cette fois-ci on a matrix au lieu de array :
>>> A
matrix([[ 1., 2.],
[ 3., 4.]]) On peut calculer la transposée d’une matrice ainsi :
>>> A.T
matrix([[ 1., 3.],
[ 2., 4.]]) Voici une matrice sur une ligne :
>>> X = matrix('5.0 7.0')
>>> X
matrix([[ 5., 7.]]) Sa transposée sera sur une seule colonne :
Y = X.T
>>> Y
matrix([[ 5.],
[ 7.]]) On peut multiplier une matrice carrée par une matrice...
Génération de graphiques
Python est un langage qui a de très nombreuses cordes à son arc. Il peut totalement être utilisé de manière impérative ou de manière objet, sans aucun problème.
En ce qui concerne la génération de graphiques, on peut donc soit faire appel à une syntaxe pythonique qui va utiliser l’objet, soit préférer une syntaxe à la MATLAB, ce qui est pratique pour les connaisseurs de ce langage, puisque cela leur évite d’avoir à réapprendre tout et d’avoir à maîtriser les concepts objet.
Pour visualiser un graphique, vous aurez besoin d’utiliser une console IPython ou, encore mieux, le IPython Notebook.
Pour ce dernier, la commande recommandée pour le lancer est :
$ ipython3 notebook --pylab inline 1. Syntaxe MATLAB
Pour dessiner un graphique, il suffit de procéder par étapes. Tout d’abord, on crée un espace linéaire :
>>> x = linspace(-5, 5, 11) Ensuite, on crée la fonction à représenter :
>>> y = x ** 2 Puis, on crée notre espace de représentation :
>>> figure() Suivi du graphique (on veut représenter y par rapport à x et on veut une ligne rouge) :
>>> plot(x, y, 'r') On peut ensuite donner un nom aux axes :
>>> xlabel('abscisse')
>>> ylabel('ordonnee') Puis donner un titre au graphique lui-même :
>>> title('fonction carree') Ensuite, vous pouvez afficher votre graphique :
>>> show() Notons que la courbe sera d’autant plus précise qu’il y aura de points. Ceci se fait en changeant l’espace linéaire de départ (et en répétant toutes les étapes) :
>>> x = linspace(-5, 5, 101)
>>> x = linspace(-5, 5, 1001) Voici le résultat :
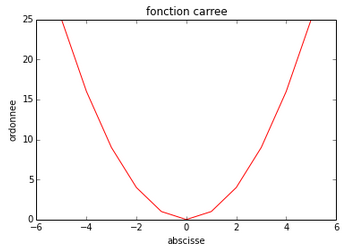
2. Syntaxe objet
Nous pouvons réaliser exactement le même type d’opération à l’aide d’une syntaxe objet :
x = linspace(-5, 5, 11)
y = x ** 2
fig = plt.figure()
axes = fig.add_axes([0, 0, 1, 1])
axes.plot(x, y, 'r')
axes.set_xlabel('abscisse')
axes.set_ylabel('ordonnee')
axes.set_title('fonction...Introduction à Pandas
1. Présentation
Pandas est une bibliothèque Python spécialisée dans le traitement, la manipulation et l’analyse de données.
Ces données sont organisées sous la forme d’un dataframe, lequel est un tableau organisé, à la manière d’un fichier CSV. Les colonnes d’un tel tableau correspondent à des variables et les lignes à des individus. Lorsque les données sont organisées sous une seule colonne, on peut utiliser la notion de série.
Pour installer Pandas, il suffit de faire :
$ pip install pandas 2. Séries
Une série est un dataframe n’ayant qu’une seule colonne, comparable à une liste Python. Il se crée d’ailleurs à partir d’une telle liste :
>>> from pandas import Series
>>> s = Series([1, 1, 2, 3, 5, 8, 13]) Chaque série est associée à un index qui, par défaut, est construit comme celui des listes :
>>> s.index
RangeIndex(start=0, stop=7, step=1) On peut ainsi adresser rapidement un élément de la série à partir de son index :
>>> s[1]
1
>>> s[4]
5
>>> s[9]
KeyError: 9 On peut également extraire une sous-série :
>>> s[2:5]
2 2
3 3
4 5
dtype: int64 On voit ici à gauche l’index et à droite la valeur. La chose essentielle à retenir est que l’index associé à la valeur reste identique au lieu d’être recréé à la volée comme ce serait le cas pour une liste. Notons que, comme toujours, on part de l’indice minimal inclus à l’indice maximal exclu. Notons également que, comme c’est le cas pour NumPy, une série est associée à un type qui est soit déterminé automatiquement, comme c’est le cas ici, soit précisé au moment de la création de la série. Dans notre exemple, nous n’avions que des entiers, on a donc un type entier. Voici d’autres exemples :
>>> Series([1, 1, 2, 3, 5, 8, 13], dtype=float).dtype
dtype('float64')
>>> Series([1... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations