Code et mathématiques
Présentation du chapitre
Nous allons parcourir ici certains rudiments ayant trait aux tenseurs ainsi que diverses notions complémentaires également utiles dans les usages liés à l’Intelligence Artificielle. L’idée générale n’est pas de vous proposer un cours ou une formation sur ce sujet très pointu, mais d’esquisser les quelques aspects qui vous permettront d’appréhender avec sérénité les textes de recherche et les tutoriels que vous croiserez dans votre parcours de data scientist.
Les syntaxes TensorFlow de base utilisées dans ce chapitre doivent être assimilées pour aborder avec sérieux le développement avec ces outils.
En première lecture, il n’est pas indispensable d’assimiler en profondeur le côté mathématique des sujets développés ici pour pouvoir aborder la suite de l’ouvrage (mais il faut assimiler le code TensorFlow).
Nous vous proposons de le parcourir attentivement. Vous pourrez mémoriser où "trouver quoi" afin de faciliter vos expériences futures.
Peu d’ouvrages, y compris en langue anglaise, sur TensorFlow 1.x ou sur des frameworks similaires prennent le temps d’explorer ces formulations mathématiques et le débutant ne possédant pas déjà une culture mathématique affirmée...
En route vers les tenseurs
1. Autour des tenseurs
La notion de tenseur se construit à partir du XIXe siècle. Très schématiquement, on peut dire qu’elle hérite de plusieurs points de vue :
-
La représentation multidimensionnelle d’informations physiques "statiques" possédant des structures complexes (par exemple en cristallographie, ou aujourd’hui dans la représentation des images ou des vidéos).
-
La représentation multidimensionnelle de phénomènes physiques possédant des structures physiques complexes (par exemple la description de toutes les contraintes sur un solide plus ou moins élastique, ceci sur chacune de ses faces).
-
La généralisation des notions d’algèbre linéaire qui s’expriment opérationnellement par les notions de vecteurs, matrices, normes, structures duales et produits scalaires.
-
La volonté de se doter de représentations efficaces et opérationnelles en algèbre multilinéaire.
-
La simplification de la manipulation des équations de la physique devant simultanément intégrer les notions d’espace, de temps, de variété (en anglais manifold), de probabilité, de courbure et de différentiation.
-
La normalisation des méthodes de calcul différentiel sur les structures multilinéaires et/ou multidimensionnelles qui débouche sur le calcul tensoriel.
Dans les ouvrages d’initiation au machine learning on présente souvent les vecteurs comme des colonnes (ou lignes) d’objets, les matrices comme des tableaux d’objets, les tenseurs comme des tableaux multidimensionnels (array) le cas échéant pouvant avoir une forme (shape). En fait, on parle ici de la forme des choses, mais moins de leur sens. Pour autant, le seul fait de ranger des informations sous forme vectorisée et/ou sous la forme d’un tensor s’avère fécond...
Les vecteurs
1. Approche intuitive des vecteurs
Sur un plan ("une feuille") ou en volume ("autour de vous"), il est assez facile d’imaginer la notion de vecteur en physique comme étant une quantité orientée ("une flèche") possédant une direction et un module ("une intensité").
Suivant les cas, ce vecteur physique peut être compris comme :
-
la caractéristique intrinsèque d’un élément du réel ; la vitesse de cet avion est de 900 km/h ( le module ) dans la direction du nord ;
-
la position d’un élément par rapport à l’origine du référentiel ; la cathédrale de Saint Denis est à 9 km au nord de Notre-Dame ;
-
la caractéristique d’une abstraction qui agit sur le réel ; ce matin à Brest le vent est de force 4, plein ouest.
Dans un espace muni d’un repère adéquat, on peut décomposer ce vecteur comme étant la combinaison linaire ("la somme pondérée") des vecteurs de la base du repère (dont, par définition, les modules respectifs ont pour valeur 1 et dont aucun vecteur composant cette base n’est colinéaire, c’est-à-dire n’a la même direction).
Pour représenter ce vecteur dans une base donnée, il est alors commode de lister les poids en question, sous la forme d’une représentation matricielle comportant une colonne de scalaires ("nombres").
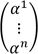
Sur un plan n vaut 2. Dans "notre" espace quotidien n vaut 3 ou 4, suivant que l’on considère ou pas la notion de positionnement temporel. Dans le cas du fichier d’entraînement du data set mnist vu au précédent chapitre n = 60000 pour le vecteur y_train.
Dans ce dernier cas, on pourrait craindre que la forme ait pris le pas sur le fond : il n’est en effet pas aisé de comprendre en quoi cette colonne de chiffre serait un "vecteur" et de quelle "base" on parle. Pourtant on constate avec l’usage que cette représentation est bien pratique et s’avère avoir un fondement mathématique explicite dans le cadre du machine learning.
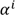 ) ou même
) ou même 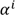 s’il n’est pas ambigu que
l’on...
s’il n’est pas ambigu que
l’on...Les matrices
D’une certaine façon, l’usage des matrices découle naturellement de la nécessité de manipuler les vecteurs : on pourrait dire que les matrices "opèrent" alors sur des vecteurs. Dans ce que les mathématiciens nomment l’algèbre linéaire cela s’avère manifestement le cas (mais il existe d’autres types de matrices, c’est-à-dire dont la signification est différente).
Ces opérations peuvent être successives et une nouvelle matrice peut alors être calculée pour exprimer cette succession d’opérations, on parle alors de multiplication matricielle. À l’inverse, une matrice compliquée peut parfois être décomposée en une multiplication de matrices plus simples ou rapides à comprendre, à manipuler ou à calculer.
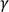 , le tangage
, le tangage 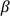 et le lacet
et le lacet 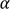 .
.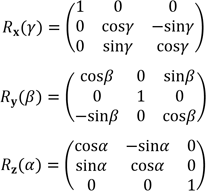
Pour mémoire, notez que la multiplication matricielle suivante de ces trois matrices permet de construire la rotation vectorielle de votre choix dans notre espace 3D orthonormé (rotation d’un vecteur autour d’un axe dirigeant la rotation en question).
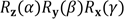
La construction d’une telle...
Les quaternions
Comme indiqué plus haut, toutes les matrices ne représentent pas des rotations. Cette remarque préliminaire va nous aider à comprendre l’utilité des quaternions.
Pour modéliser, ou calculer les mouvements d’un objet physique (caméra, robots…), on doit souvent effectuer de nombreuses rotations sucessives (mais pas seulement !).
C’est le cas par exemple quand on modélise l’articulation du bras d’un robot (ou celle de votre coude !). Ces rotations successives ne sont pas toujours toutes situées sur le même plan et peuvent être appliquées en nombre (imaginez qu’un moteur applique une micro rotation toutes les 100 millisecondes). Elles se composent donc au travers de multiplications de matrices numériques.
Malheureusement, dans la réalité les opérations numériques successives peuvent dégrader le résultat, et bien que mathématiquement une composition de matrices de rotation donne une matrice de rotation, on obtient parfois une matrice résultante qui n’est plus une matrice de rotation.
Afin de corriger ce phénomène, on peut procéder de deux façons :
-
Utiliser des représentations numériques en virgules flottantes de plus en plus précises.
-
Ou, dans le cas précis des rotations successives, utiliser une représentation...
Les tenseurs
1. Exemples de formes d’un tenseur
Dans un outil comme TensorFlow, la forme d’une image en gamme de gris telle que celle du fichier nmist que nous avons manipulée au deuxième chapitre est naturellement (28,28). Si l’on considère une image couleur, codée en Rouge, Vert, Bleu, cela multiplie par 3 couches, une par couleur.
Un tenseur comportant ces 3 dimensions (indices) que sont la largeur, la hauteur et la couleur, ne comprenant que des valeurs nulles est assez facile à fabriquer. Il pourra servir de réceptacle à une telle image.
im = K.zeros( # création d'un tenseur variable
shape = (3,28,28), #
dtype = tf.int32 # encodage entiers 32, pas très économe!
)
print("\n shape d'une image \n",K.shape(im)) shape d'une image
tf.Tensor([ 3 28 28], shape=(3,), dtype=int32) Pour bien comprendre comment est structuré un tel tenseur, je vous propose de vous imprégner du suivant, assez petit pour être édité. L’idée est d’observer attentivement ce qui a été créé pour une forme donné, ici (3,4,2).
im = K.zeros( # création d'un tenseur variable
shape = (3,4,2), #
dtype = tf.int32 # encodage entier
)
print("\n 3 couches de 4 lignes de 2 colonnes : \n",im) 3 couches de 4 lignes de 2 colonnes :
<tf.Variable 'Variable:0' shape=(3, 4, 2) dtype=int32, numpy=
array([[[0, 0],
[0, 0],
[0, 0],
[0, 0]],
[[0, 0],
[0, 0],
[0, 0],
[0, 0]],
[[0, 0],
[0...Différentiation
Ne pas confondre cette différentiation avec un "t", qui est une opération mathématique et différenciation avec un "c" qui traite de l’établissement d’une différence entre les choses…
TensorFlow comporte une aptitude très utile, nommée la différentiation automatique, que nous verrons à la section Différentiation automatique (AD).
Dans vos calculs, et quand vous lirez un article de recherche ou la description d’un algorithme, il faudra identifier avec soin la nature des fonctions manipulées ainsi que le type des coordonnées employées et les bases dans lesquelles sont exprimées ces coordonnées.
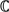 ) :
) :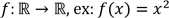 ;
;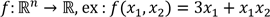 ;
;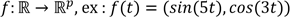 (ici une
courbe paramétrée) ;
(ici une
courbe paramétrée) ;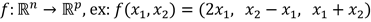 .
.1. Introduction
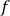 d’une seule variable
du corps des réels, dire que cette fonction est dérivable
autour du point
d’une seule variable
du corps des réels, dire que cette fonction est dérivable
autour du point  signifie
qu’un petite variation autour de
signifie
qu’un petite variation autour de  génère approximativement par
génère approximativement par 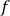 une petite variation proportionnelle (le o représente une quantité négligeable à l’endroit
considéré - voir plus loin) :
une petite variation proportionnelle (le o représente une quantité négligeable à l’endroit
considéré - voir plus loin) :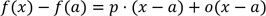
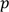 , qui est en fait la pente de la tangente de
la courbe en x = a ,
est appelée dérivée de
, qui est en fait la pente de la tangente de
la courbe en x = a ,
est appelée dérivée de 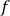 en
en  . Cette quantité étant
calculable en plusieurs lieux, on peut construire une nouvelle fonction
"dérivée" au travers de ce mécanisme.
Nous verrons plus loin que TensorFlow nous permet de calculer cette
fonction en plusieurs points.
. Cette quantité étant
calculable en plusieurs lieux, on peut construire une nouvelle fonction
"dérivée" au travers de ce mécanisme.
Nous verrons plus loin que TensorFlow nous permet de calculer cette
fonction en plusieurs points. peut se noter de différentes façons,
citons :
peut se noter de différentes façons,
citons :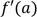
ou :
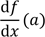
ou, bien plus explicite :
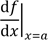
 et est de plus appliquée en
et est de plus appliquée en  .
.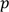 par la dérivée) :
par la dérivée) :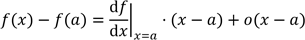
Gradient
Imaginez vous à mi-chemin du sommet d’une montagne de forme conique. Si vous cheminez autour de la montagne sans changer de courbe de niveau, vous ne descendez ni ne montez.
Si on appelle f la fonction qui représente la hauteur de la surface de la montagne en fonction de la lattitude et de la longitude de l’endroit où l’on se trouve, on peut affirmer que localement, à chacun de vos pas sur la même courbe de niveau la variation de f reste nulle le long de ce chemin.
À l’inverse si vous décidez d’aller droit vers le sommet, de façon perpendiculaire aux courbes de niveaux, la variation à chacun de vos pas sera importante et positive. La descente de la montagne correspondrait à un valeur négative. Enfin si vous décidez de monter gentiment en suivant un chemin en spirale vous aurez à chaque pas une variation positive mais faible.
On en retient que la valeur de la variation dépend de la direction dans laquelle on mesure celle-ci (direction qui peut être symbolisée par un vecteur attaché à l’endroit où l’on se trouve, c’est donc un champ vectoriel).
Nous allons maintenant aborder des concepts que vous trouverez dans les différents articles. Notre intention étant d’immuniser le lecteur pas très "matheux" en l’exposant à diverses notations qu’il pourra démystifier, mais aussi de rappeler aux autres lecteurs quelques points clés.
1. Dérivée suivant une direction et introduction des dérivées partielles
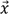 votre position sur la carte qui comprend deux
coordonnées et
votre position sur la carte qui comprend deux
coordonnées et 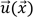 le vecteur unitaire (i.e. de
norme 1) comprenant trois coordonnées qui correspond à votre
direction dans l’espace à chacun de vos pas, on
peut former (i.e. concevoir) la fonction dérivée
locale suivant la direction
le vecteur unitaire (i.e. de
norme 1) comprenant trois coordonnées qui correspond à votre
direction dans l’espace à chacun de vos pas, on
peut former (i.e. concevoir) la fonction dérivée
locale suivant la direction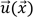 au point
au point 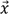 :
: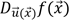
C’est une fonction à valeurs réelles (scalaires) qui désigne l’intensité...
Tenseur métrique
Ce qu’il faut comprendre ici c’est que les notions abordées sont très locales (i.e. autour de chaque point d’un éventuel parcours, comme quand nous cheminions de pas en pas en gravissant la montagne de l’introduction). Le fait de travailler sur des dérivées, qui sont par nature linéaires, montre que l’on approxime la surface en chaque point en évoluant sur les divers plans tangents en ces points (c’est plus ou moins la notion de géométrie riemannienne à condition que l’on dispose d’une métrique).
Évidemment, par plan on désigne ici l’hyperplan de même dimension que la variété (une variété de 3D plongée dans un espace 4D est "tangente" a un hyperplan en 3D : un hyperplan possède une dimension de moins que l’espace considéré et peut être réprésenté par une équation linéaire simple).
On retrouve également cette notion quand on considère les surfaces de décision de divers algorithmes de machine learning sur lequelles nous nous basons pour séparer une classe d’une autre.
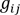 , c’est...
, c’est...Optimisation
Dans la suite de l’ouvrage nous évoquerons différentes techniques d’optimisation, souvent liées à la recherche d’une situation où l’erreur commise sera minimale. On pourait reformuler cela en exprimant qu’il faut trouver un jeu de paramètres qui minimise (c’est-à-dire optimise) l’erreur.
L’idée est souvent d’effectuer un parcours sur une variété en cherchant un point particulier qui correspond à l’optimum que l’on cherche.
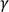 qui minimise
(ou maximise) une fonction d’un champ de tenseurs
qui minimise
(ou maximise) une fonction d’un champ de tenseurs  en fonction de certaines contraintes, typiquement
l’appartenance ou la non apartenance à une variété ou à ses
voisinages.
en fonction de certaines contraintes, typiquement
l’appartenance ou la non apartenance à une variété ou à ses
voisinages.Dans de nombreux cas, la fonction à minimiser est notre fonction de perte loss en respectant des contraintes de structure heureusement simples qui peuvent alors s’exprimer par plusieurs inégalités ou plusieurs égalités :
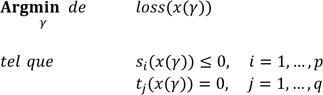
Par Argmin ou Argmax on entend deux recherches concomittantes :
|
1. |
La recherche d’un optimum de
 , en faisant varier le jeu de paramètres , en faisant varier le jeu de paramètres 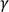 . . |
|
2. |
La recherche de l’image réciproque de cet optimum, qui est un ensemble, parfois réduit à un jeu unique de paramètres (dans un espace à trois dimensions comme... |
Boîte à outils complémentaire
1. Filtre de Kalman
Cet outil permet d’estimer l’état d’un système linéaire composé d’états additifs et comportant du bruit.
On a d’une part le processus lui-même qui peut être entaché d’un bruit, puis la mesure du processus entachée de son propre bruit. On considère que ce sont des bruits blancs.
La mécanique d’implémentation est récursive, typique du concept de filtre (on utilise les valeurs précédentes pour trouver les nouvelles valeurs). Ce concept s’apparente à la notion de convolution que nous aborderons au chapitre Améliorations du modèle.
Pour comprendre le concept, il suffit d’imaginer un problème d’interception : à partir des positions successives d’un mobile qui suit une certaine trajectoire (mais comportant des aléas affectant cette trajectoire et les outils de mesure de la trajectoire) l’intercepteur est contraint de prédire la suite de la trajectoire pour pouvoir procéder à l’interception.
Il existe des généralisations pour des cas non linéaires (filtre Kalman étendu - FKE). L’équation d’état a alors l’aspect suivant :
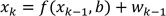
 k représente
l’état du vecteur d’état à la
période k, comme
par exemple la position du mobile cité en exemple. b est un vecteur de paramètres
entachés d’une incertitude.
k représente
l’état du vecteur d’état à la
période k, comme
par exemple la position du mobile cité en exemple. b est un vecteur de paramètres
entachés d’une incertitude. 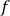 est une fonction représentant la dynamique du
système, le cas échéant non linéaire. wk représente le bruit blanc
bruitant le signal.
est une fonction représentant la dynamique du
système, le cas échéant non linéaire. wk représente le bruit blanc
bruitant le signal.L’équation correspondant à la mesure est la suivante :
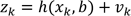
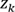 est le vecteur
mesuré,
est le vecteur
mesuré, 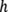 représente
de fait les caractéristiques de la mesure,
représente
de fait les caractéristiques de la mesure, 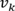 le bruit blanc bruitant la mesure (les 2 bruits
ne sont pas corrélés). Évidement ni la
mesure , ni les paramètres, ni le bruit de la mesure ne
ne dépendent des mesures...
le bruit blanc bruitant la mesure (les 2 bruits
ne sont pas corrélés). Évidement ni la
mesure , ni les paramètres, ni le bruit de la mesure ne
ne dépendent des mesures...Bibliographie du chapitre
Houchmandzadeh, Bahram. 2018. "Mathématiques pour la Physique. Licence. Mathématiques pour la Physique." https://hal.archives-ouvertes.fr/cel-01148916v5.
Laaraiedh, Mohamed. 2012. "Implementation of Kalman Filter with Python Language." CoRR abs/1204.0375. http://arxiv.org/abs/1204.0375.
Prieur, Benoit. 2019. Informatique quantique. 1st ed. Éditions ENI.
Ruder, Sebastian. 2016. "An overview of gradient descent optimization algorithms," September. http://arxiv.org/abs/1609.04747.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
