Fonctions de manipulation des courbes de taux
Introduction
Dans ce chapitre vous allez créer les fonctions vous permettant de manipuler des courbes de taux. Vous allez d’abord réaliser une fonction permettant de changer les conventions utilisées pour un taux. Vous verrez par la suite les fonctions d’interpolation linéaire et cubique. Vous aurez alors les éléments pour construire une courbe de facteurs d’actualisation ou de taux zéro-coupon. Pour finir vous verrez une fonction pour calculer un taux forward.
L’instruction "Option Base"
Avant d’aborder les fonctions de manipulations des taux, nous allons expliquer une option déclarée au niveau du module, de la même manière que "Option Explicit".
L’instruction "Option Base" suivie de 0 ou 1, permet de déclarer la valeur par défaut de l’indice inférieur d’un tableau.
Par exemple, il est équivalent de faire :
Option Base 1
Function Test()
Dim UnTableau(10)
End Function
et
Function Test()
Dim UnTableau(1 To 10)
End Function
Vous ajouterez cette option sur les prochains modules. Sur le module contenant les fonctions de manipulations des dates, elle ne doit pas être présente.
La fonction ChangeTaux
Les taux peuvent prendre différentes formes. Ils peuvent être de la forme simple, aussi appelés taux proportionnels, de forme actuariels ou taux composés ou encore être des taux continus.
Taux simple
Dans le cas d’un taux simple, les intérêts i reçus pour la période allant de t à t+1 par un taux r pour un investissement de 100 sont calculés par la formule :: i=100*r*FractionAnnee(t,t+1,Base)
Taux composé
Dans le cas des intérêts composés, ou capitalisés, les intérêts payés en n sont supposés réinvestis dans le capital de l’instrument. En n+1, les intérêts seront calculés sur le capital augmenté des intérêts payés en n.
Par exemple, pour un instrument payant des intérêts annuels, à la fin de la première période le capital C1 sera le capital initial C0 augmenté des intérêts i :
C1=C0+i*C0=C0(1+i)
À la deuxième période :
C2=C1+i*C1=C1(1+i)=C0(1+i)2
Et ainsi de suite :
Cn=C0(1+i)n
Si le paiement n’est pas annuel, mais à une périodicité p inférieure à l’année (p=12 pour un paiement mensuel), on conserve l’idée de la capitalisation, la formule générale devient :
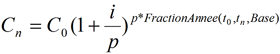
Il est possible de calculer des taux équivalents. Par exemple, le taux semi-annuel i2 équivalent au taux annuel i est calculé par la relation :
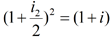
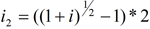
Taux continu
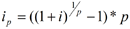 alors il est
démontré que :
alors il est
démontré que :ip=ln(1+i).
ip est appelé taux continu.
Facteur d’actualisation
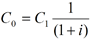 , le rapport
, le rapport 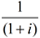 est appelé facteur d’actualisation.
est appelé facteur d’actualisation.Il permet de connaître la valeur actuelle d’un montant futur. Les facteurs d’actualisation sont la base des techniques d’évaluation des instruments financiers.
Objectif de la fonction ChangeTaux
Cette fonction permet la conversion d’un taux ou d’un facteur d’actualisation en un autre taux (ou facteur d’actualisation) en modifiant la base de calcul et/ou son type. Elle sera utile pour calculer une courbe de facteurs d’actualisation pour la valorisation des instruments et également pour calculer...
La fonction InterpolationLineaire
Pour valoriser un instrument, ou déterminer ces flux, il est nécessaire de pouvoir déterminer les taux d’intérêts à toutes les dates futures. Comme il n’existe pas sur les marchés de taux pour chaque date, il faut recourir à des interpolations des taux existants. La méthode la plus simple est l’interpolation linéaire.
Objectif
Cette fonction calcule les taux ou les facteurs d’actualisation interpolés linéairement pour un vecteur de date.
Par exemple, en utilisant cette courbe de taux :
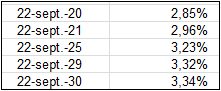
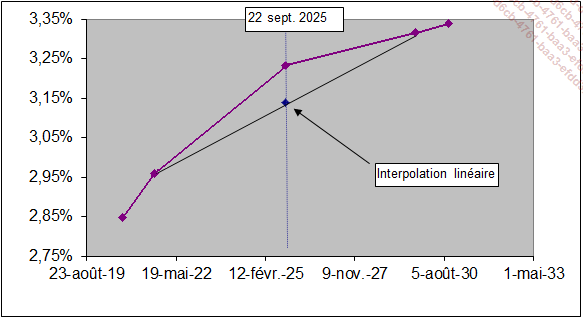
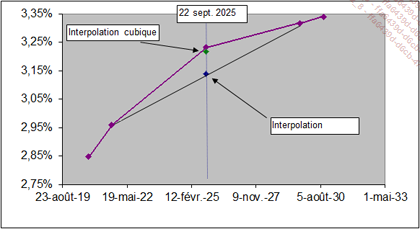
La recherche du taux au 22 septembre 2025 par interpolation linéaire sur la droite passant par le taux du 22 septembre 2021 et du 22 septembre 2029, donne la valeur 3.14%.
Graphique 7 : Interpolation linéaire
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
TableauMaturites |
Dates de maturité des données, triées par ordre croissant |
Tableau de Dates |
|
TableauDonnees |
Données : taux en pourcentage ou facteurs d’actualisation |
Tableau de Doubles |
|
DateCalculees |
Dates pour lesquelles il faut interpoler les données |
Tableau de Dates |
|
TypeDonnees |
Type de données (optionnel) |
Booléen, égal à 1 si les données sont des facteurs d’actualisation |
|
DateDeCalcul |
Date de calcul (optionnel) |
Obligatoire si les données sont des facteurs d’actualisation |
Mode de calcul
Cas général
Pour chaque date à calculer Dc, il faut trouver dans le tableau de maturités les 2 dates Dinf et Dsup encadrant Dc, puis interpoler le taux Tc de Dc par une interpolation sur la droite passant par les taux Tinf de Dinf et Tsup de Dsup :
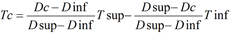
Cas des bornes
Dans le cas où le type de donnée est "Taux", si la date Dc est inférieure à la première date de maturité disponible, alors Tc est égal au taux de la première maturité disponible.
Dans le cas où le type de donnée est "Taux", si la date Dc est supérieure à la dernière date de maturité disponible, alors Tc est égal au taux de la dernière maturité disponible.
Dans le cas où les données sont des facteurs d’actualisation, si la date Dc est inférieure à la première date de maturité disponible...
La fonction InterpolationCubique
Objectif
Cette fonction calcule les taux ou les facteurs d’actualisation par interpolation cubique pour un vecteur de dates.
Une méthode moins rustique d’interpolation est l’interpolation cubique. Elle consiste à utiliser une équation de degré trois passant par les quatre points encadrant la date recherchée.
En reprenant les données de l’exemple de la fonction InterpolationLineaire, la valeur interpolée au 22 septembre 2025 est 3.22%.
Graphique 8 : Interpolation linéaire et interpolation cubique
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
TableauMaturites |
Dates de maturité des données, triées par ordre croissant |
Tableau de Dates |
|
TableauDonnees |
Données : taux en pourcentage ou facteurs d’actualisation |
Tableau de Doubles |
|
DateCalculees |
Dates pour lesquelles il faut interpoler les données |
Tableau de Dates |
|
TypeDonnees |
Type de données (optionnel) |
Booléen, égal à 1 si les données sont des facteurs d’actualisation |
|
DateDeCalcul |
Date de calcul (optionnel) |
Obligatoire si les données sont des facteurs d’actualisation |
Mode de calcul
Cas général
Pour chaque date à calculer Dc, il faut trouver dans le tableau de maturités les quatre dates encadrant Dc :
D1<D2<Dc<D3<D4
Connaissant les taux T1 à T4 correspondant aux dates D1 à D4, le taux T de Dc est calculé en utilisant l’équation :
T=a* Dc³ + b* Dc² + c* Dc+d
Où a, b, c et d sont déterminés par le système :
T1=a* D1³ + b* D1² + c* D1+d
T2=a* D2³ + b* D2² + c* D2+d
T3=a* D3³ + b* D3² + c* D3+d
T4=a* D4³ + b* D4² + c* D4+d
La résolution de ce système de quatre équations à quatre inconnues est :

Traitements des bornes
Le traitement des bornes s’effectue en utilisant la fonction InterpolationLineaire.
Code de la fonction InterpolationCubique
Les fonctions de calculs matriciels disponibles dans les feuilles de calcul n’ont pas d’équivalent en VBA. Il est possible d’y accéder en utilisant la propriété WorksheetFunction de l’objet...
La fonction Interpolation
Pour pouvoir appeler indifféremment l’une des deux méthodes d’interpolation sans alourdir le code de nos prochaines fonctions, il est nécessaire de les encapsuler dans une seule fonction, qui appellera l’une ou l’autre méthode en fonction d’un argument.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
TableauMaturites |
Dates de maturité des données, triées par ordre croissant |
Tableau de Dates |
|
TableauDonnees |
Données : taux en pourcentage ou facteurs d’actualisation |
Tableau de Doubles |
|
DateCalculees |
Dates pour lesquelles il faut interpoler les données |
Tableau de Dates |
|
TypeInterpolation |
Type interpolation (optionnel) |
Booléen, égal à 1 si l’interpolation se fait linéairement |
|
TypeDonnees |
Type de données (optionnel) |
Booléen, égal à 1 si les données sont des facteurs d’actualisation |
|
DateDeCalcul |
Date de calcul (optionnel) |
Obligatoire si les données sont des facteurs d’actualisation |
Code de la fonction
Function Interpolation(TableauMaturites, TableauDonnees,
DateCalculees, _
Optional TypeInterpolation As Boolean = False, _
Optional TypeDonnees As Boolean = False, Optional _
...La fonction CourbeActualisation
Objectif
Pour pouvoir déterminer la valeur d’un instrument, il faut sommer la valeur actuelle de chacun de ses flux. Vous devez construire une courbe permettant de déterminer pour chaque date future le facteur d’actualisation. Pour construire cette courbe vous allez utiliser un panier d’instruments de marché. Sur la partie inférieure à 1 an, vous utiliserez des instruments monétaires. Ces produits paient un coupon à leur date de maturité. Puis, vous utiliserez le taux des contrats Futures de type euribor. Ces contrats sont cotés sous la forme 100-taux. Enfin, sur la partie longue, vous utiliserez le taux de rendement des obligations à taux fixe à paiement annuel, ou des taux de swap.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
TableauDatesValeurs |
Dates de valeur des instruments futures |
Tableau de Dates |
|
TableauMaturites |
Dates de maturité des données, triées par ordre croissant |
Tableau de Dates |
|
TableauDonnees |
Données : taux en pourcentage ou facteurs d’actualisation |
Tableau de Doubles |
|
TableauTypeDonnees |
Type de données : "MM" pour instrument du marché monétaire, "FUT" pour les futures, "PAR" pour les obligations ou les swaps |
Tableau de chaînes de caractères |
|
TableauBases |
Bases de calcul des instruments |
Tableau de type Variant |
Mode de calcul
La transformation des taux monétaires ("MM") en facteur d’actualisation est directe. La valeur future d’un investissement initial V0 au taux r à la date t1 est :
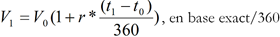
Vous pouvez déterminer la valeur actuelle, V0, d’un montant V1 à la date t1 par :
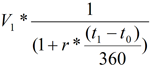
Le facteur d’actualisation de la période t0 à t1 est donc :
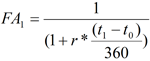
L’utilisation des contrats Futures ("FUT") ou contrats à terme est plus délicate. Un contrat à terme nous indique le taux qui aura cours pour la période allant de t1 à t2. Sous l’hypothèse d’absence d’opportunité d’arbitrage, un investissement de t0 à t1 au taux r0,1, puis le réinvestissement du montant perçu en t1 jusqu’en t2 au taux r1,2 est équivalent à un investissement au taux r0,2 sur la période...
La fonction TauxForward
Objectif
Cette fonction calcule un taux forward à partir d’une courbe de facteurs d’actualisation. Elle nous permettra de déterminer les flux d’un instrument à taux variable.
Un taux forward est un taux dont la date de début de la période d’application est une date dans le futur.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
TableauMaturites |
Dates de maturité des données, triées par ordre croissant |
Tableau de Dates |
|
TableauDonnees |
Facteurs d’actualisation |
Tableau de Doubles |
|
DateDepart |
Date de départ d’application du taux forward |
Date |
|
DateFin |
Date de fin d’application du taux forward |
Date |
|
iType |
Type du taux |
Entier |
|
iFrequence |
Fréquence de paiement du taux |
Entier |
|
Base |
Base du taux |
Variant |
Mode de calcul
En reprenant la formule générale de la fonction CourbeActualisation pour le cas des instruments "PAR" à paiement annuel :
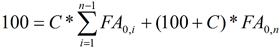
Si la date de départ t0, est forward, alors la valeur actuelle de l’instrument n’est pas 100, mais la valeur actualisée de 100 :
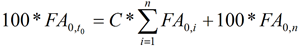
Le taux C de l’instrument forward est donc :
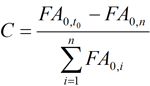
Dans le cas où l’instrument a plusieurs paiements par an, la formule devient :
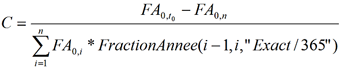
Pour ramener ce taux dans les conventions souhaitées, vous utiliserez la fonction ChangeTaux.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

