Instruments à taux fixe
Introduction
Vous allez dans ce chapitre réaliser un ensemble de fonctions utiles pour la gestion des instruments à taux fixe.
Un instrument à taux fixe paye à intervalles réguliers des intérêts basés sur le même taux tout au long de sa vie. Le montant des intérêts peut ne pas être constant.
Par exemple les obligations de l’Etat français, les OAT, sont des instruments à taux fixe. Pour plus d’informations sur les obligations, vous pouvez consulter l’article qui leur est consacré sur Wikipédia, à l’adresse : http://fr.wikipedia.org/wiki/Obligation_(finance)
Nous ne considérons que les instruments à remboursement in fine, c’est-à-dire dont le flux de capital est unique et à la date de maturité de l’instrument.
La fonction FluxTF
Objectif
Cette fonction détermine les dates et les flux d’un instrument à taux fixe entre la date de calcul et la date de maturité.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblValeurRemboursement |
Valeur de remboursement |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Si les flux ne sont pas ajustés selon leur durée, les paiements d’intérêts sont tous égaux :
Flux(i)=dblValeurRemboursement*Coupon/iFrequence
Pour un investissement de 100 € recevant un coupon de 5% par an, payé en 2 fois, les flux d’intérêts seront de 2.5 €.
Si les flux sont ajustés selon leur durée, par exemple en mode Modified Following, il faut pondérer chaque flux par la fonction FractionAnnee :
dblFrac=FractionAnnee(DateFlux(i-1);DateFlux(i);ModeAjustement)
Flux(i) = dblValeurRemboursement*Coupon*dblFrac
Que les flux d’intérêts soient ajustés ou non, le dernier flux de l’instrument est égal au flux d’intérêts plus le flux de remboursement.
Code de la fonction FluxTF
Pour déterminer la date des flux nous utilisons...
La fonction CouponCouruTF
Objectif
Cette fonction détermine le coupon couru entre la date du dernier coupon et la date de calcul. Elle nous permettra de distinguer le prix avec ou sans coupon couru.
Le prix d’une obligation incluant son coupon couru est le prix plein coupon ou dirty price.
Le prix d’une obligation excluant son coupon couru est le prix pied de coupon ou clean price.
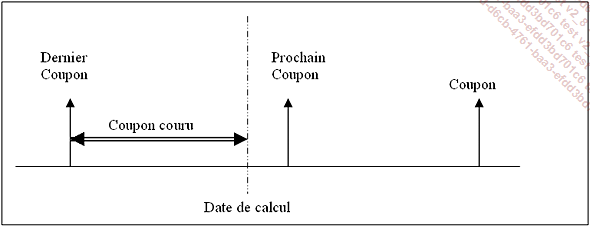
Pour en savoir plus sur les coupons courus vous pouvez consulter la section Coupon couru de l’article de Wikipédia sur les obligations à l’adresse suivante : http://fr.wikipedia.org/wiki/Obligation_(finance)
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblValeurRemboursement |
Valeur de remboursement |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Le coupon couru est égal à la fraction des intérêts acquis depuis le dernier paiement....
La fonction TauxRendementTF
Objectif
Cette fonction détermine le taux de rendement actuariel d’une obligation.
Le taux de rendement actuariel est le taux d’actualisation qui permet de retrouver le prix plein coupon d’un instrument à taux fixe.
La courbe des taux est considérée comme plate. Chaque flux est actualisé au même taux.
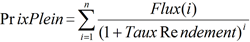
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblPrixPied |
Prix pied de coupon de l’instrument |
Double |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblValeurRemboursement |
Valeur de remboursement |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Il faut chercher le taux t applicable afin que la somme des flux actualisés à ce taux soit égale au prix plein coupon de l’instrument :
dblFrac(i) = FractionAnnee(i-1;i;Base)
PrixPlein = dblPrixPied+CouponCouru
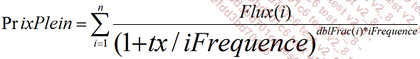
Pour ce faire vous utiliserez la méthode de Newton, décrite sur Wikipedia à l’adresse http://fr.wikipedia.org/wiki/Methode_de_Newton
Posez :
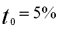
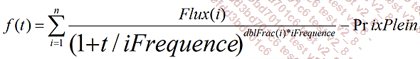
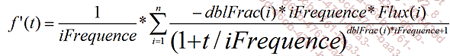
Itérez 100 fois avec :
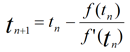
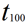 .
.Code de la fonction TauxRendementTF
Pour gagner en vitesse d’exécution, les fractions d’années sont calculées une fois et conservées dans un tableau. La précision de la fonction peut être améliorée en augmentant le nombre de fois que la boucle est exécutée.
Function TauxRendementTF(DateDeCalcul...La fonction PrixPleinTF
Objectif
Cette fonction détermine le prix plein coupon d’un instrument à taux fixe à partir de son taux de rendement actuariel.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblTauxRendement |
Taux de rendement de l’instrument |
Double |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblValeurRemboursement |
Valeur de remboursement |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Comme vous l’avez vu pour la fonction TauxRendement, le prix plein coupon est égal à la somme des flux actualisés au taux de rendement.
dblFrac(i) = FractionAnnee(i-1;i;Base)
Code de la fonction PrixPleinTF
Le code de la fonction est similaire à celui de la fonction TauxRendement.
Function PrixPleinTF(DateDeCalcul As Date, DateDeMaturite As Date, _
dblTauxRendement As Double, dblCoupon As Double, _
...La fonction PrixPiedTF
Objectif
Cette fonction détermine le prix pied de coupon d’une obligation. Celui-ci est égal au prix plein coupon diminué du coupon couru.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblTauxRendement |
Taux de rendement de l’instrument |
Double |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblValeurRemboursement |
Valeur de remboursement |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Le prix plein coupon est égal à la somme des flux actualisés au taux de rendement.
dblFrac(i) = FractionAnnee(i-1;i;Base)

Le prix pied de coupon est égal au prix plein diminué du coupon couru.
PrixPied = PrixPlein - CouponCouru
Code de la fonction PrixPiedTF
Vous avez réalisé une fonction calculant le prix plein, une fonction calculant le coupon couru, il ne reste plus qu’à effectuer la soustraction.
Function PrixPiedTF(DateDeCalcul...La fonction SpreadSurCourbeTF
Objectif
Cette fonction est utile pour valoriser les obligations émises par les entreprises. Ce type d’instrument aussi appelé instrument de crédit se valorise par rapport à la courbe taux des swaps. Il faut déterminer la constante, qui une fois ajoutée aux taux d’actualisation permet de retrouver le prix de marché. Cette constante est appelée spread par les professionnels, elle est l’indicateur du risque de cet instrument. Plus le spread est élevé, plus le risque de défaut de paiement est grand.
Un spread est une constante à ajouter aux taux de la courbe pour retrouver le prix de marché d’une obligation.
Cette fonction détermine le spread à appliquer à une courbe de taux zéro coupon, calculée avec la fonction CourbeActualisation, pour retrouver le prix d’une obligation.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblPrixPied |
Prix pied de coupon de l’instrument |
Double |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblValeurRemboursement |
Valeur de remboursement |
Double |
|
TabDateFA |
Tableau des maturités des facteurs d’actualisation |
Variant |
|
TabFA |
Tableau des facteurs d’actualisation |
Variant |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Il faut chercher le spread à appliquer aux facteurs d’actualisation permettant d’égaliser la somme des flux actualisés au prix plein coupon de l’instrument :

Comme dans le cas de la fonction TauxRendement, vous utilisez la méthode de Newton.
Posez :
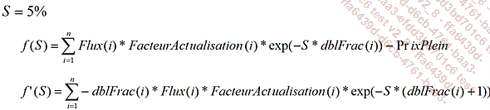
Itérez 100 fois avec :
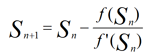
Le spread est égal à S100.
Code...
La fonction PrixPleinSurCourbeTF
Objectif
Cette fonction détermine le prix plein coupon d’une obligation à partir d’une courbe de facteurs d’actualisation. Plutôt que de considérer la courbe des taux plate, comme dans le cas de la fonction PrixPleinTF, où le taux d’actualisation est identique pour chaque flux, ici les taux d’actualisation proviennent d’une courbe de facteurs d’actualisation, déterminée à partir d’instruments de marché. Vous pouvez choisir d’appliquer un spread aux facteurs d’actualisation, pour par exemple, valoriser un titre d’entreprise (corporate bond).
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblValeurRemboursement |
Valeur de remboursement |
Double |
|
TabDateFA |
Tableau des maturités des facteurs d’actualisation |
Variant |
|
TabFA |
Tableau des facteurs d’actualisation |
Variant |
|
dblSpread |
Spread (optionnel) |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Vous actualiserez les flux de l’instrument en utilisant les facteurs d’actualisation, éventuellement augmenté du spread, déterminé par la fonction CourbeActualisation.
dblFrac(i) = FractionAnnee(DateDeCalcul;i;Base)...
Les fonctions de gestion du risque d’un instrument à taux fixe
La valeur d’un instrument de taux est fonction des taux d’intérêts. Anticiper la variation de la valeur permet d’anticiper le risque de perte et de couvrir ce risque. Vous allez construire dans cette partie les fonctions permettant de déterminer les variations de la valeur de l’instrument à une variation des taux d’intérêts.
La variation du prix P d’un titre suite à une variation du taux de rendement de r à r’, peut être déterminée localement par un développement limité au deuxième ordre :
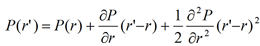
Les grandeurs principalement utilisées sont :
-
La sensibilité S ;
La sensibilité est la variation relative du prix à une variation du taux de rendement.
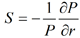
-
La convexité C ;
La convexité mesure la variation relative de la sensibilité en fonction du taux de rendement.
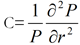
-
La duration D ;
La duration est la durée de vie moyenne actualisée des flux.
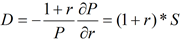
Vous pouvez obtenir plus de détails sur ces grandeurs sur le site de l’encyclopédie Wikipedia.
La fonction BPVTF
Objectif
Cette fonction détermine la variation de prix d’une obligation pour une variation du taux de rendement. C’est la dérivée première du prix par rapport au taux de rendement. Les initiales BPV correspondent à Basis Point Value.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblTauxRendement |
Taux de rendement de l’instrument |
Double |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblValeurRemboursement |
Valeur de remboursement |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Cette fonction correspond à la dérivée première du prix, PrixPlein’(t) par rapport à son taux de rendement t, pour 0.01% :
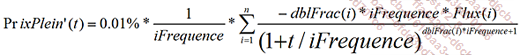
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

