Fonctions de manipulation des swaps
Introduction
Nous examinerons les swaps de taux fixe contre taux variables.
Dans un swap de taux, deux contreparties échangent des flux d’intérêts. L’une reçoit des flux à taux fixe et paie des flux à taux variables, l’autre reçoit les flux à taux variables et paie les flux à taux fixe.
Un swap est donc la somme d’un instrument à taux fixe de nominal N et un instrument à taux variables de nominal -N.
La plupart des fonctions de manipulations des swaps ne sont donc que la somme des fonctions correspondantes d’un instrument à taux fixe et d’un instrument à taux variables, mais dont les nominaux sont opposés. En exemple vous verrez la fonction de calcul du prix sur une courbe de taux. Nous nous arrêterons également sur les fonctions de BPVP par maturité et de flux de l’instrument car elles font intervenir des manipulations de tableaux.
D’autres fonctions sont spécifiques aux swaps comme par exemple le calcul du taux fixe d’un swap ou du spread sur taux variables. Nous examinerons également ces fonctions.
La fonction PrixPleinCbSwp
Objectif
Cette fonction détermine le prix plein coupon d’un swap par actualisation de ses flux sur une courbe de taux.
Arguments
La liste des arguments pour un swap est longue car elle reprend les arguments d’un instrument à taux fixe et celle d’un instrument à taux variables.
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateCalcul |
Date de calcul |
Date |
|
DateMaturite |
Date de maturité de l’instrument |
Date |
|
dblCpFixe |
Coupon de la jambe fixe (%) |
Double |
|
iFrequenceJF |
Fréquence de la jambe fixe, nombre de coupon par an de la jambe fixe |
Entier |
|
BaseJF |
Base la jambe fixe |
Variant |
|
dblNominal |
Valeur de remboursement, si elle est positive alors les flux de la jambe fixe sont reçus et ceux de la jambe variable sont payés. Si la valeur de remboursement est négative, alors les flux de la jambe variable sont reçus et ceux de la jambe fixes sont payés. |
Double |
|
iFrequenceJV |
Fréquence de la jambe variable. Nombre de coupon par an de la jambe variable |
Entier |
|
BaseJV |
Base |
Variant |
|
TabDateFA |
Tableau des maturités des facteurs d’actualisation |
Variant |
|
TabFA |
Tableau des facteurs d’actualisation |
Variant |
|
dblDernierFixing |
Dernier fixing s’il est connu (%, optionnel) |
Double |
|
iPeriodeTV |
Période d’application du taux variable, si elle est différente de la fréquence de paiement. Par exemple un taux 6 mois payé tous les 3 mois, alors iFrequence=12/3=4 et iPeriodeTV=6 (nombre de mois). Par défaut iPeriodeTV=12/iFrequence (Optionnel) |
Entier |
|
bSetInArrears |
1 si l’instrument est "Set in arrears" (optionnel, par défaut=0) |
Booléen |
|
dblSpread |
Spread à ajouter aux coupons de la jambe variable (optionnel) |
Double |
|
ModeAjustementJV |
Mode d’ajustement de la jambe variable (optionnel) |
Variant |
|
ModeAjustementJF |
Mode d’ajustement de la jambe fixe (optionnel, par défaut identique à celui de la jambe variable) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein sur la jambe fixe (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon... |
La fonction BPVCbSwap
Objectif
La fonction BPVCbSwap détermine les variations de valeur d’un swap, pour des variations de 1 point de base (0.01%) de chaque taux d’actualisation.
Arguments
Les arguments sont identiques à ceux de la fonction PrixPleinCbSwp.
Mode de calcul
Comme pour le calcul du prix, la BPV sur courbe est égale à la somme des BPV de chaque jambe, en utilisant des valeurs de remboursement opposées. L’unique difficulté est qu’ici, vous devez manipuler des tableaux.
Code de la fonction BPVCbSwp
Comme les tableaux renvoyés par les fonctions pour la jambe fixe et la jambe variable ont la même dimension, il suffit d’étirer chaque dimension des tableaux pour les sommer.
Function BPVCbSwp(DateCalcul As Date, DateMaturite As Date, _
dblCpFixe As Double, _
iFreqJF As Integer, BaseJF, dblNominal As Double, _
iFreqJV As Integer, BaseJV, _
TabDateFA, TabFA, Optional dblDernierFixing As Double = 0, _
Optional iPeriodeTV As Integer = 0, _
Optional bSetInArrears As Boolean = False, _
Optional dblSpread As Double = 0, _
Optional ModeAjustementJV As Variant = 0, _
Optional...La fonction FluxSwp
Objectif
Cette fonction détermine les dates et les flux d’un swap entre la date de calcul et la date de maturité.
Arguments
Les arguments sont identiques à ceux de la fonction PrixPleinCbSwp.
Mode de calcul
Les flux du swap sont égaux à ceux de sa jambe fixe déterminés avec la fonction FluxTF et ceux de sa jambe variable sont déterminés avec la fonction FluxTV.
Pour une meilleure lisibilité, nous distinguerons dans deux colonnes les flux de la jambe fixe et ceux de la jambe variable.
Code de la fonction
Nous allons regrouper dans un seul tableau, FluxSwap, les données provenant de la fonction FluxTF et celles provenant de la fonction FluxTV. Nous trierons ensuite le tableau FluxSwap par ordre croissant des dates. Si deux lignes possèdent la même date, nous sommerons ses éléments. Pour trier le tableau nous utiliserons le tri à bulles.
Le tri à bulles
Le tri à bulles consiste à comparer deux lignes d’un tableau et, dans notre cas, faire remonter les lignes (dates) les plus petites, comme une bulle d’air remonte à la surface. Un exemple d’implémentation pour un tableau à une dimension est :
|
|
|
Boucle à effectuer tant que le tableau n’est pas trié. |
|
On suppose le tableau trié. |
|
Boucle sur l’ensemble des éléments du tableau. |
|
Compare deux lignes du tableau. |
|
Si les lignes ne sont pas en ordre croissant, échange des lignes. |
|
Si on passe sur cette ligne, c’est que le tableau n’est pas trié. |
|
Le tri à bulles n’est pas l’algorithme de tri le plus rapide, mais c’est certainement le plus simple à mettre en œuvre.
Code
Function FluxSwp(DateCalcul As Date, DateMaturite As Date, _
dblCpFixe As Double, _
iFreqJF As Integer, BaseJF, dblNominal As Double, _
iFreqJV As Integer, BaseJV, _
...La fonction TauxFixeSwap
Objectif
Cette fonction détermine le taux fixe d’un swap permettant d’égaliser le prix de la jambe fixe et le prix de la jambe variable.
Arguments
Les arguments sont identiques à ceux de la fonction PrixPleinCbSwp, sauf l’argument dblCpFixe qui n’est pas renseigné.
Mode de calcul
Le prix de la jambe fixe, c’est-à-dire la somme de ses flux actualisés, doit être égal au prix de la jambe variable :
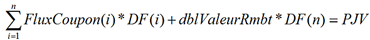
Avec DF(i) le facteur d’actualisation à la date i et PJV le prix de la jambe variable.
Les flux de coupons sont égaux au coupon fixe multiplié par des cœfficients d’ajustement des coupons. Par exemple, pour un coupon fixe payé deux fois par an, sans ajustement pour les jours fériés, les cœfficients seront à 0.5.
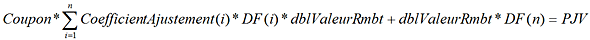
Et donc :
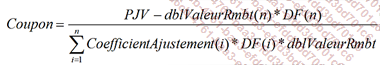
Code de la fonction TauxFixeSwp
Les cœfficients d’ajustement sont calculés par la fonction FluxTF, avec un coupon de 100% et un nominal de 1. Le nominal de 1 doit être déduit du dernier flux.
Les facteurs d’actualisation des flux sont obtenus par la fonction interpolation.
Le prix de la jambe variable, PJV, est obtenu en utilisant la fonction PrixPleinSurCourbeInsTV.
Function TauxFixeSwp(DateCalcul As Date, DateMaturite As Date, _
iFreqJF As Integer, BaseJF, dblNominal As Double, _
...La fonction SpreadSwp
Objectif
Cette fonction détermine le spread à ajouter aux coupons de la jambe variable d’un swap, pour égaliser le prix de la jambe fixe et de la jambe variable.
Arguments
Les arguments sont identiques à ceux de la fonction PrixPleinCbSwp, sauf l’argument dblSpread qui n’est pas renseigné.
Mode de calcul
Sachant que :
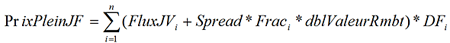
Avec
|
Fraci = FractionAnnee(datei-1,datei,base) |
|
|
PrixPleinJF |
Le prix plein coupon de la jambe fixe. |
|
Et |
|
|
FluxJVi |
Le flux de la jambe variable à la date i. |
Alors le spread est égal à :

Code de la fonction SpreadSwp
Le prix plein de la jambe fixe est donné par la fonction PrixPleinSurCourbeTF et le spread est déterminé par la fonction SpreadSurCourbeInsTV.
Function SpreadSwp(DateCalcul As Date, DateMaturite As Date, _
dblCpFixe As Double, _
iFreqJF As Integer, BaseJF, dblNominal As Double, _
iFreqJV As Integer, BaseJV, _
TabDateFA, TabFA, Optional dblDernierFixing As Double = 0, _
Optional iPeriodeTV As Integer = 0, _
Optional bSetInArrears As Boolean = False, _
Optional ModeAjustementJV As Variant = 0, _
Optional ModeAjustementJF As Variant = -1, _
... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

