Fonctions pour les titres indexés sur l'inflation
Introduction
Cette partie concerne plus précisément les OATi. Ces instruments ont leur coupon et leur nominal réindexés annuellement pour tenir compte de l’évolution de l’indice des prix. La valeur de remboursement du capital des OATi ne peut pas être inférieure à la valeur nominale. Le coupon indexé des OATi peut être inférieur au coupon avant indexation.
Par exemple, si IPCref est l’indice des prix à la consommation lors de l’émission d’une OATi et IPCi l’indice des prix à la consommation à la date i, alors les flux d’une OATi de coupon c et de nominal M sont à chaque date de coupon :
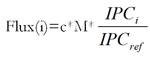
À la date de maturité, il faut ajouter le flux de remboursement égal à :
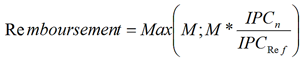
La fonction Max renvoie la valeur maximale entre M et M indexé.
Pour pouvoir valoriser une OATi, il faut pouvoir déterminer l’indice des prix pour toute date i, vous verrez avec la fonction IndicePrixQuotidien comment interpoler les indices de prix mensuels pour déterminer une valeur quotidienne.
En plus des fonctions de calcul du coupon couru, du prix ou du taux de rendement, nous verrons comment calculer le break even (ou inflation point mort), l’inflation point mort est le taux d’inflation constant à appliquer aux flux d’une OATi pour retrouver son prix.
La fonction ValeurIndiceQuotidien
Objectif
Cette fonction retourne la valeur de l’indice des prix à une date donnée selon les conventions de calcul des OATi.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
IPCM3 |
Indice des prix 3 mois avant le mois de la date de calcul |
Double |
|
IPCM2 |
Indice des prix 2 mois avant le mois de la date de calcul |
Double |
Mode de calcul
La valeur de l’indice des prix quotidien à la date de calcul est :
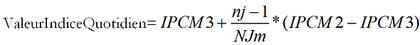
Avec :
NJm=le nombre de jour du mois de la date de calcul
nj=numéro du jour de la date de calcul
Code de la fonction
Function ValeurIndiceQuotidien(DateDeCalcul As Date, _
IPCM3 As Double, IPCM2 As Double)
'//////////////////////////////////////////////////////////
' Cette fonction détermine la valeur
' de l'indice à la date de calcul
' par interpolation selon les conventions des OATi
'//////////////////////////////////////////////////////////
Dim dblIPC As Double 'Donnée renvoyée
Dim dblNJM As Integer 'Nombre de jour dans le mois de calcul
Dim dblNJ As Double 'Numéro du jour du mois de calcul
dblNJM = DateSerial(Year(DateDeCalcul), Month(DateDeCalcul) + 1, 1) - _
...La fonction CouponCouruIndexe
Objectif
Cette fonction détermine le coupon couru entre la date du dernier coupon et la date de calcul.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblCoupon |
Coupon (%), coupon de l’instrument |
Double |
|
iFrequence |
Fréquence, nombre de coupon par an de l’instrument |
Entier |
|
Base |
Base |
Variant |
|
dblNominal |
Valeur de remboursement |
Double |
|
IPCREF |
Indice des prix de référence de l’instrument |
Double |
|
IPCM3 |
Indice des prix à la consommation 3 mois avant la date de calcul |
Double |
|
IPCM2 |
Indice des prix à la consommation 2 mois avant la date de calcul |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Le coupon couru est indexé de la croissance de l’indice des prix depuis l’émission de l’instrument jusqu’à la date de calcul.
-
Coupon Couru Titre Indexe=CC* VIQ/ IPCREF
-
Avec CC le coupon couru non indexé
-
VIQ l’indice des prix interpolé à la date de calcul
Code de la fonction CouponCouruIndexe...
La fonction BreakEven
Objectif
Cette fonction détermine le break even, ou inflation point mort, d’un titre indexé.
L’inflation point mort est le taux d’inflation constant à appliquer sur la durée de vie résiduelle de l’instrument pour retrouver son prix de marché.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblPrixPlein |
Prix plein coupon de l’instrument |
Double |
|
dblTauxRendement |
Taux de rendement de l’instrument |
Double |
|
dblCoupon |
Coupon (%), coupon de l’instrument |
Double |
|
iFrequence |
Fréquence, nombre de coupon par an de l’instrument |
Entier |
|
Base |
Base |
Variant |
|
dblNominal |
Valeur de remboursement |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Si tous les indices des prix étaient connus, le prix d’un instrument indexé serait :
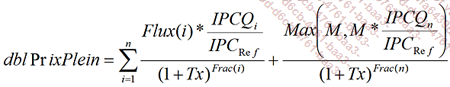
Avec :
|
Flux(i) |
le flux de coupon de l’instrument à la date i. |
|
IPCQi |
l’indice des prix interpolé à la date i. |
|
IPCref |
l’indice des prix de référence de l’instrument. |
|
Frac(i) |
la fraction d’année entre la date de calcul et la date i. |
|
M |
la valeur de remboursement (nominal) de l’instrument. |
|
Tx |
le taux de rendement de l’instrument. |
Comme les indices des prix futurs sont inconnus, on cherche à déterminer le taux d’inflation constant permettant de réconcilier la somme des flux actualisés et le prix de l’instrument.

Avec :
|
P |
l’inflation point mort ou break even. |
Pour déterminer l’inflation point mort, nous utilisons la méthode de Newton.
Soit :
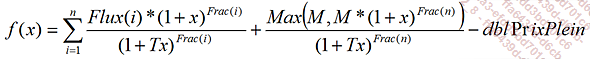
Et :
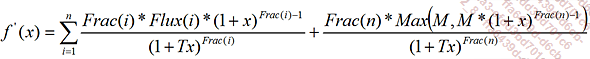
On pose :
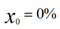
On itère 100 fois avec :
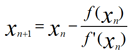
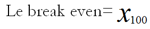
Code de la fonction BreakEven
Plutôt que d’utiliser la fonction Max pour déterminer le flux de nominal, nous effectuons un test sur le signe de x.
Function BreakEven(DateDeCalcul As Date, DateDeMaturite As Date, _
dblPrixPlein As Double, _
dblTauxRendement As Double, dblCoupon...La fonction BreakEvenCb
Objectif
Cette fonction détermine l’inflation point mort d’un titre indexé en utilisant une courbe de facteurs d’actualisation plutôt qu’un taux de rendement.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblPrixPlein |
Prix plein coupon de l’instrument |
Double |
|
dblCoupon |
Coupon (%), coupon de l’instrument |
Double |
|
iFrequence |
Fréquence, nombre de coupon par an de l’instrument |
Entier |
|
Base |
Base |
Variant |
|
dblNominal |
Valeur de remboursement |
Double |
|
TabDateFA |
Tableau des maturités des facteurs d’actualisation |
Variant |
|
TabFA |
Tableau des facteurs d’actualisation |
Variant |
|
dblSpread |
Spread (optionnel) |
double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
La méthode est la même que pour la fonction BreakEven, mais pour actualiser les flux, nous utilisons les facteurs d’actualisation de TabFA, plutôt qu’un taux de rendement. Par conséquent, les fonctions deviennent :
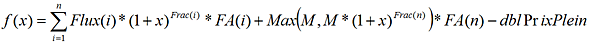
Et :
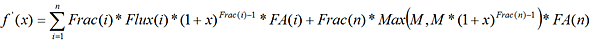
Avec FA(i), le facteur d’actualisation à la date i.
On pose :
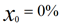
On itère 100 fois avec :
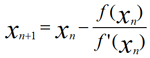
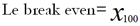
Code de la fonction BreakEvenCb
Function BreakEvenCb(DateDeCalcul As Date, DateDeMaturite As Date, _
dblPrixPlein As Double, _
dblCoupon As Double, _
iFrequence As Integer, Base As Variant, dblNominal As Double, _
TabDateFA, TabFA, Optional dblSpread As Double = 0, _
Optional ModeAjustement As Variant = 0, _
Optional bPremierCouponPlein As Boolean = False, _
Optional TypeCouponBrise As Variant = 0, _
Optional DateDeDepart As Date = 0)
'////////////////////////////////////////////////////////// ...La fonction PrixPleinIndexe
Objectif
Cette fonction détermine le prix plein coupon d’un instrument indexé.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblTauxRendement |
Taux de rendement de l’instrument |
Double |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblNominal |
Valeur de remboursement |
Double |
|
dblBreakEven |
Taux d’inflation point mort |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Comme vous l’avez vu pour la fonction BreakEven le prix plein de l’instrument s’écrit :
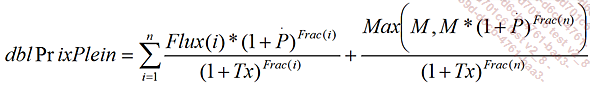
Avec :
|
P |
l’inflation point mort ou break even. |
|
Flux(i) |
le flux de coupon de l’instrument à la date i. |
|
Frac(i) |
la fraction d’année entre la date de calcul et la date i. |
|
M |
la valeur de remboursement (nominal) de l’instrument. |
|
Tx |
le taux de rendement de l’instrument. |
Code de la fonction PrixPleinIndexe
Function PrixPleinIndexe(DateDeCalcul As Date, DateDeMaturite As Date, _
dblTauxRendement As Double, _
dblCoupon As Double, _
iFrequence As Integer, Base As Variant, dblNominal As Double, _
dblBreakEven As Double, _
Optional...La fonction PrixPleinCbIndexe
Objectif
Cette fonction détermine le prix plein coupon d’un instrument indexé par actualisation de ses flux sur une courbe de taux.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblPrixPlein |
Prix plein coupon de l’instrument |
Double |
|
dblCoupon |
Coupon (%), coupon de l’instrument |
Double |
|
iFrequence |
Fréquence, nombre de coupon par an de l’instrument |
Entier |
|
Base |
Base |
Variant |
|
dblNominal |
Valeur de remboursement |
Double |
|
dblBreakEven |
Inflation point mort de l’instrument |
Double |
|
TabDateFA |
Tableau des maturités des facteurs d’actualisation |
Variant |
|
TabFA |
Tableau des facteurs d’actualisation |
Variant |
|
dblSpread |
Spread (optionnel) |
double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Le mode de calcul est similaire à celui de la fonction PrixPleinIndexe, sauf que l’actualisation des flux se fait grâce à des facteurs d’actualisation.
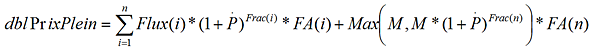
Avec :
|
P |
l’inflation point mort ou break even. |
|
Flux(i) |
le flux de coupon de l’instrument à la date i. |
|
Frac(i) |
la fraction d’année entre la date de calcul et la date i. |
|
M |
la valeur de remboursement (nominal) de l’instrument. |
|
FA(i) |
le facteur d’actualisation à la date i. |
Code de la fonction PrixPleinCbIndexe
Function PrixPleinCbIndexe(DateDeCalcul As Date, _
DateDeMaturite As Date, _
dblCoupon As Double, _
iFrequence As Integer, Base As Variant, dblNominal As Double, _
dblBreakEven As Double, _
TabDateFA, TabFA, Optional dblSpread As Double = 0, _
Optional...La fonction TauxRendementInsIndexe
Objectif
Cette fonction détermine le taux de rendement d’un instrument indexé, permettant d’égaliser la somme des flux actualisés avec ce taux et le prix du titre.
Arguments
|
Nom de l’argument |
Description |
Format de l’argument |
|
DateDeCalcul |
Date de calcul |
Date |
|
DateDeMaturite |
Date de maturité de l’instrument |
Date |
|
dblCoupon |
Coupon (%) |
Double, coupon de l’instrument |
|
iFrequence |
Fréquence |
Entier, nombre de coupon par an de l’instrument |
|
Base |
Base |
Variant |
|
dblNominal |
Valeur de remboursement |
Double |
|
dblBreakEven |
Taux d’inflation point mort |
Double |
|
ModeAjustement |
Mode d’ajustement (optionnel) |
Variant |
|
bPremierCouponPlein |
Premier Coupon Plein (optionnel) |
Booléen |
|
TypeCouponBrise |
Type coupon brisé (optionnel) |
Variant |
|
DateDeDepart |
Date de départ de l’instrument (optionnel, obligatoire si le type de coupon brisé est renseigné) |
Date |
Mode de calcul
Comme pour un instrument à taux fixe, vous utiliserez la méthode de Newton, avec comme fonction :
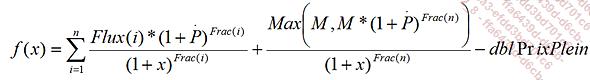
Et :
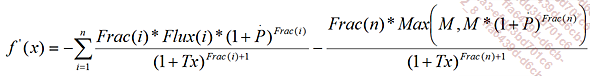
Avec :
|
P |
l’inflation point mort ou break even. |
|
Flux(i) |
le flux de coupon de l’instrument à la date i. |
|
Frac(i) |
la fraction d’année entre la date de calcul et la date i. |
|
M |
la valeur de remboursement (nominal) de l’instrument. |
On pose :
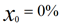
On itère 100 fois avec :
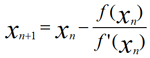
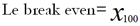 .
.Code de la fonction TauxRendementInsIndexe
Les fonctions f(x) et f’(x) sont ajustés pour tenir compte de la fréquence de paiement des coupons.
Function TauxRendementInsIndexe(DateDeCalcul As Date, _
DateDeMaturite As Date, _
dblPrixPlein As Double, _
dblBreakEven As Double, dblCoupon As Double, _
iFrequence As Integer, Base As Variant, dblNominal As Double, _
Optional ModeAjustement As Variant = 0, _
Optional bPremierCouponPlein As Boolean = False, _
Optional TypeCouponBrise As Variant = 0, _
Optional DateDeDepart As Date = 0)
'////////////////////////////////////////////////////////// ... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

