Décision en avenir incertain : arbre de probabilité, simulation Monte-Carlo
La méthode de l’arbre de probabilité
Principe
Un arbre de probabilité est un outil d’aide à la décision en avenir incertain. Il représente un ensemble de décisions sous la forme graphique d’un arbre.
Pour rendre le modèle utile pour la prise de décision, il est possible d’inclure dans l’arbre les dépenses et les résultats estimés pour chacune des décisions. Chaque extrémité de l’arbre, les branches représentent un résultat potentiel.
Dans le but de représenter l’incertitude liée aux résultats de chacune des décisions prises, la probabilité de chaque évènement est ajoutée aux branches de l’arbre.
À partir de là, il sera possible de calculer l’espérance mathématique.
L’espérance mathématique est égale à la somme des gains (et des pertes) pondérées par la probabilité du gain (ou de la perte).
Elle représente l’espérance de gain que nous pouvons « espérer ».
Une des meilleures illustrations de l’espérance de gain se trouve dans le jeu de poker.
Imaginons qu’avec les cartes que j’ai en mains, j’ai 80 % de chance de gagner. J’ai mis 5 € dans le pot, l’autre joueur a aussi mis 5 €.
D’après mes cartes, j’ai 80 % de chance de gagner. Si c’est le cas, j’empoche la totalité du pot, soit 10 €. Cela représente un gain net de 5 €.
J’ai 20 % de chance de perdre, si c’est le cas, je perds la totalité du pot, soit 10 €, pour une perte nette de 5 €.
L’espérance mathématique de gain est :
80 % x 5 + 20 % x (-5) = 3
Cette situation est donc profitable, l’espérance mathématique est positive. Il s’agit en quelque sorte « d’un bon pari ».
C’est le même principe que nous allons utiliser, mis à part que dans notre arbre de décision, du fait du caractère séquentiel des décisions, nous allons utiliser des probabilités combinées.
Application avec Excel
La société Elena souhaite mettre...
La simulation Monte-Carlo
Principe
La simulation Monte-Carlo propose d’analyser la variabilité d’un résultat en utilisant un grand nombre de valeurs possibles pour un ou plusieurs paramètres intervenant dans le calcul de ce résultat.
Les valeurs prises par les paramètres peuvent être soit totalement aléatoires, soit générées aléatoirement selon une distribution de probabilité, si cette dernière est connue ou estimée.
Dans la pratique, la distribution de probabilité peut être estimée en analysant les données historiques de l’entreprise, d’une entreprise de même type ou bien d’un même secteur.
Après l’examen des résultats d’une simulation Monte-Carlo, l’analyste est souvent capable de faire des recommandations de décisions sur les variables contrôlables en ayant une idée de l’espérance du résultat, mais aussi de sa variabilité.
Cette méthode est utilisée dans de nombreuses disciplines allant de la physique à la finance. Elle a été utilisée pour la première fois durant la deuxième guerre mondiale dans le cadre du projet Manhattan. « Monte-Carlo » était le nom de code utilisé pour cette méthode, faisant référence au casino de Monte-Carlo et au caractère incertain des jeux de hasard.

Stanislaw Ulam à gauche et John von Neumann à droite : les mathématiciens, inventeurs de la simulation Monte-Carlo.
Exemple et application avec Excel
Le café Bob a décidé de tenter de diversifier son activité, en plus des glaces et des cafés, le gérant souhaite se lancer dans la vente de petits pains.
Le coût du petit pain serait de 0,90 €.
Le prix de vente du petit pain serait de 1,30 €.
Il existe une association d’aide et de collecte alimentaire qui se chargerait de récupérer les invendus du jour au prix de 0,50 €.
Ayant une expérience dans la boulangerie et après plusieurs sondages auprès de sa clientèle actuelle, Bob estime que les ventes de petits pains journaliers suivraient la distribution de probabilité suivante :
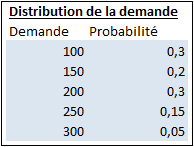
À partir de ces éléments...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations




