Outils statistiques de prévisions
Introduction
Dans ce chapitre, nous allons étudier quelques-uns des outils statistiques les plus utilisés en pratique pour établir une prévision.
Il s’agit de méthodes utilisant des données historiques de l’entreprise. En d’autres termes, nous allons nous fier au passé pour tenter de prévoir le futur.
Si ce travail est important, il ne constitue en fait que la moitié d’un travail prédictif efficace. En effet, pour mener son analyse, l’entreprise doit aussi réaliser un travail qualitatif sur les aspects économiques de son marché et de son environnement :
Quelle est ma part de marché ?
À quelle étape de cycle de vie se trouve mon produit ?
Comment les mutations technologiques affectent-elles mon secteur ?
Quel est l’état de la concurrence ?
Quelle est la conjoncture macroéconomique actuelle ?
Etc.
Bien entendu, dans un ouvrage consacré à l’analyse financière avec Excel, c’est surtout l’aspect statistique de la prévision qui va nous intéresser.
La régression linéaire
Principe
La régression est probablement l’outil statistique le plus utilisé pour établir des prévisions. Le but de la régression est d’estimer la relation qu’il existe entre deux ou plusieurs variables.
Si le modèle a une seule variable explicative, il s’agit d’une régression linéaire simple. Dans le cas où le modèle à plusieurs variables explicatives, nous parlerons d’une régression linéaire multiple.
Il est possible de faire des régressions linéaires avec des variables numériques ou catégorielles.
Enfin, toutes les régressions ne sont pas linéaires, selon la relation qu’il existe entre les données, il pourra s’agir de régressions non linéaires.
Cette méthode doit son nom à Francis Galton, mathématicien, statisticien et sociologue anglais qui fut un des premiers à l’utiliser, notamment pour tenter de prédire, en 1888, la taille d’un enfant à l’âge adulte en fonction de la taille de ses parents.

Francis Galton 1822 - 1911
Aujourd’hui, la régression linéaire est utilisée dans toute sorte de domaines : prévisions commerciales, finances d’entreprise, finances de marché, dans le domaine de la santé, dans les études économiques, sociologiques... En outre, il s’agit de l’un des algorithmes les plus utilisés en data sciences/machine learning.
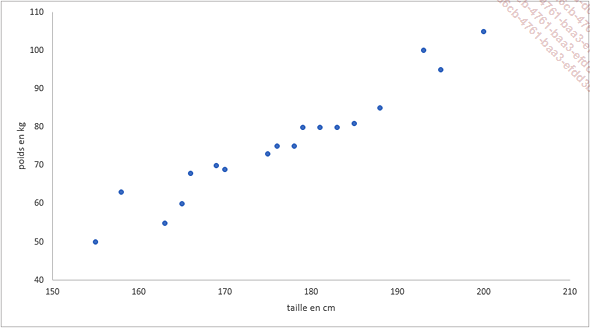
Cet exemple est un graphique en nuage de points représentant sur l’axe des abscisses, la taille en centimètres d’individus et sur l’axe des ordonnées leur poids en kilo.
Même s’il existe des personnes plus lourdes ou plus légères que la moyenne, il est probable qu’il y ait une relation entre le poids et la taille des individus.
Si nous tentons de tracer une droite représentant la tendance de ce graphique, plusieurs points seront en dessous de cette droite, d’autres seront au-dessus et quelques points seulement se retrouveront sur la droite.
La meilleure droite de régression possible, celle qui capturera au mieux la tendance de nos données...
La régression linéaire simple : application avec Excel
Le directeur d’un magasin de jouets pense que le chiffre d’affaires mensuel de son magasin est directement corrélé aux dépenses mensuelles réalisées en publicité.
Il souhaiterait déterminer quel pourrait être son chiffre d’affaires pour une dépense mensuelle en publicité de 19 000 €.
Pour cela, le directeur a répertorié les données correspondant à ces deux éléments pour les vingt-quatre derniers mois.
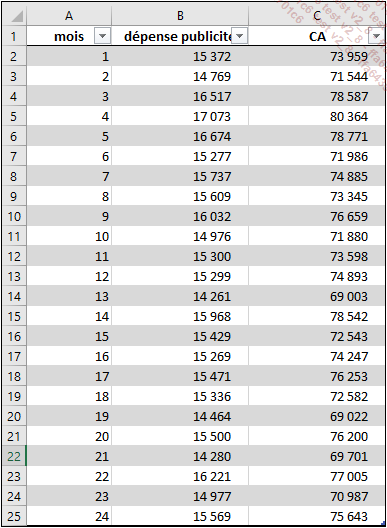
Bien entendu, d’autres facteurs peuvent entrer en ligne de compte : le prix des jouets ou la saison par exemple. Mais pour ce premier exemple, nous allons créer une régression linéaire uniquement à partir de deux variables :
Variable indépendante : le montant mensuel des dépenses en publicité
Variable dépendante : le chiffre d’affaires mensuel
Vous retrouverez le fichier contenant les données de cet exemple ainsi que les différentes méthodes de résolution dans le fichier reg_lineaire.
Première étape : représentation graphique des données
Nous allons représenter nos données avec un graphique en nuage de points.
Sélectionnez les colonnes CA et dépense publicité du tableau de données.
Dans le ruban, cliquez sur l’onglet Insertion et dans le groupe Graphiques, sélectionnez Nuages de points.
A priori, visuellement, il existerait bien une corrélation positive entre le chiffre d’affaires et les dépenses mensuelles en publicité.
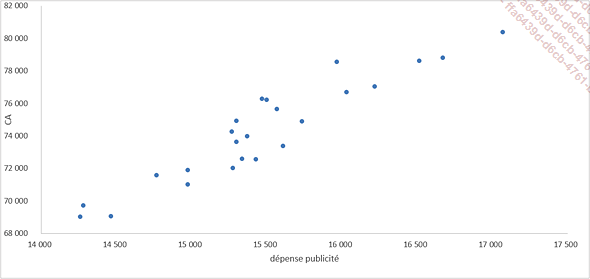
Toujours d’après la forme du nuage de points, il semblerait que la relation entre les deux variables pourrait être approximée par une régression linéaire.
Deuxième étape : calcul des éléments de la régression
Première méthode : à partir des formules d’Excel
Vous retrouverez la résolution de cette application dans l’onglet méthode formules du fichier reg_lineaire.
Le coefficient directeur peut être calculé avec la fonction PENTE.
Dans l’onglet données, sélectionnez la cellule F5.
Cliquez sur le bouton Insérer...
La régression linéaire multiple
Concept
La régression linéaire multiple utilise les mêmes principes que la régression linéaire simple, mis à part que, dans ce cas, on utilisera deux ou plusieurs variables explicatives.
L’équation d’une régression linéaire multiple peut être écrite :
y = a1x1 + a2x2..... anxn + b
où
y est la variable dépendante, aussi appelée variable expliquée. Il s’agit de la variable dont le modèle va tenter d’expliquer le mieux possible la variabilité.
x1,x2,xn sont les variables indépendantes, aussi appelées prédicteurs ou variables explicatives. Il s’agit des données qui vont servir au modèle pour tenter d’expliquer la variabilité de y.
a1,a2,an sont les coefficients directeurs associés à chacune des différentes variables indépendantes.
b est l’ordonnée à l’origine de la droite.
Contrairement au nuage de points en deux dimensions qui représente graphiquement la mesure de deux variables liées, il n’est pas aisé de faire une représentation graphique d’une régression multiple.
Dans le cas où il y a deux variables indépendantes, il est toutefois possible de créer un nuage de points en trois dimensions :
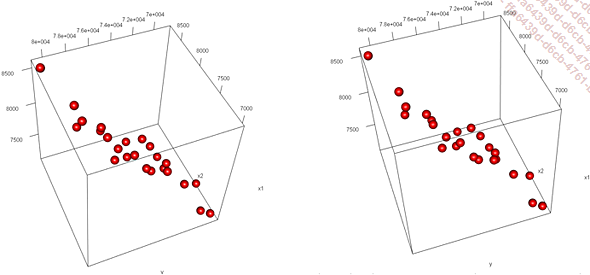
Au-delà...
La régression linéaire avec variables catégorielles
Concept
Une variable catégorielle aussi appelée variable qualitative, est tout simplement une variable sur laquelle il n’est pas possible de faire un calcul. Cela peut être par exemple :
-
Le genre : femme/homme
-
Des données géographiques : Est/Nord/Sud/Ouest
-
Des nationalités
Contrairement aux variables numériques, pour faire une régression linéaire avec des variables catégorielles, il va falloir utiliser une technique spéciale : la technique de la variable muette (dummy variable).
Comme il n’est pas possible de faire des calculs avec des variables catégorielles, nous allons utiliser un code qui ressemble au code binaire
|
Femme/Homme |
||
|
Nom |
Homme |
Femme |
|
Elena |
0 |
1 |
|
Bob |
1 |
0 |
Dans la colonne Homme, nous avons attribué la valeur 1 à la ligne Bob pour signifier qu’il s’agit d’un homme et dans la colonne femme, nous avons attribué la valeur 1 à la ligne Elena pour signifier qu’il s’agit d’une femme.
Il est possible de simplifier le tableau précédent de la manière suivante :
|
Femme/Homme |
|
|
Nom |
Femme |
|
Elena |
1 |
|
Bob |
0 |
Elena a la valeur 1 dans la colonne Femme, et Bob a la valeur 0, signifiant qu’il ne s’agit pas d’une femme (et donc c’est forcément un homme).
Le principe est le même avec quatre variables catégorielles.
|
Région habitée |
|||
|
Nom |
Est |
Ouest |
Nord |
|
Elena |
0 |
0 |
1 |
|
Bob |
0 |
0 |
0 |
Dans cet exemple, Elena habite dans la région Nord et Bob n’habite pas dans la région Est ni dans la région Ouest ni dans la région Nord. Il habite donc forcément dans la région Sud.
Application avec Excel
Un magasin de jouets investit régulièrement dans des campagnes de publicité internet et papier. Récemment, le magasin a particulièrement centré ses campagnes publicitaires sur deux modèles de jouet.
Le directeur du magasin souhaiterait déterminer lequel des deux médias est le plus susceptible d’améliorer son chiffre d’affaires pour chacun des deux modèles de jouet. Il souhaiterait en outre estimer quel serait son chiffre...
Pour aller plus loin : les régressions non linéaires
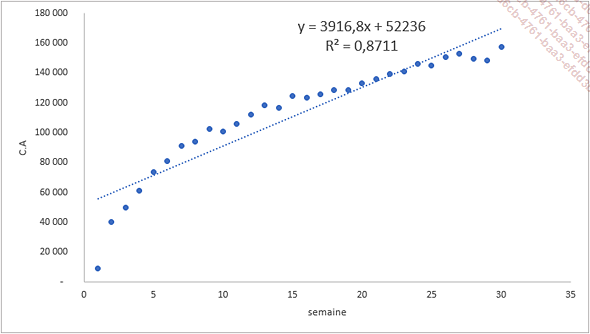
Dans l’exemple de l’onglet reg_linéaire du fichier reg_non_lineaire.xlsx, la droite de régression linéaire a un coefficient de détermination R² de 0,8711.
Même si le modèle explique bien la relation entre les semaines et le chiffre d’affaires, en regardant attentivement la forme du nuage de points, il apparaît qu’une équation de type logarithmique serait plus pertinente.
Pour réaliser ce graphique :
Sélectionnez les cellules C1:D31, dans le ruban, allez dans l’onglet Insertion, dans le groupe Graphiques, cliquez sur Insérer un nuage de points (X,Y) ou un graphique en bulles puis choisissez le graphique Nuages de points.
Sélectionnez le graphique en nuage de points obtenu, les onglets Création de graphique et Mise en forme apparaissent.
Dans l’onglet Création de graphique sélectionnez Ajouter un élément graphique, dans Courbe de tendance, sélectionnez Autres options de la courbe de tendance. Le volet Format de courbe de tendance apparaît à droite de l’écran.
Dans le menu Format de courbe de tendance, allez dans Options de courbe de tendance. Cochez Linéaire et Afficher l’équation sur le graphique, Afficher le coefficient de détermination (R²)...
Les moyennes mobiles
Principe
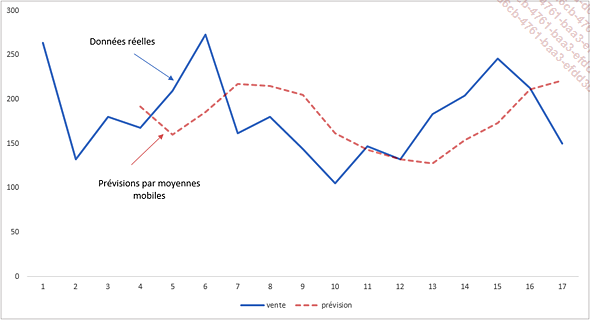
La méthode des moyennes mobiles est une méthode de lissage basée sur l’idée de faire des prévisions d’après la moyenne des valeurs observées des dernières périodes.
Puisque cette méthode part du principe que les observations futures vont être similaires aux dernières observations, les moyennes mobiles sont plutôt utilisées pour faire des prédictions à court terme.
Cette méthode consiste à faire une prévision à partir de la moyenne des N dernières observations.
Exemple :
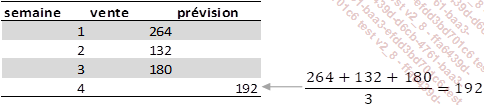
Si N est égal à 3, nous allons faire la moyenne des 3 premières valeurs pour faire une prédiction de la quatrième valeur.
Intérêt
La méthode des moyennes mobiles et les méthodes de lissage en général peuvent aider à distinguer les mouvements dus au hasard des changements fondamentaux de la tendance dans une série chronologique. Il sera ainsi possible d’une part de déterminer si la tendance de la série chronologique augmente, diminue ou reste au même niveau et d’autre part, de se servir de cette tendance pour réaliser des prévisions.
Exemple :
Il a fait exceptionnellement froid durant le mois de janvier, de ce fait, les clients ont été moins enclins à sortir pour réaliser des achats. Le temps s’est amélioré par la suite, les clients ayant reporté leurs achats en janvier, les ont réalisés au cours de février et mars.
En effectuant une moyenne des observations des mois de janvier, février et mars, il est possible d’avoir une meilleure idée de la tendance générale des ventes pour réaliser une prévision du niveau des ventes durant le mois d’avril.
Plus la période prise en compte dans le calcul des moyennes mobiles sera élevée, plus la prévision sera dépendante d’observations anciennes. Le modèle...
Les moyennes mobiles pondérées
Principe
Dans certains cas, et selon l’activité de l’entreprise, il est souhaitable d’avoir un modèle prédictif dans lequel les dernières observations réelles ont plus d’importance dans la détermination des prévisions que les valeurs plus anciennes. Dans la méthode des moyennes mobiles pondérées, un coefficient ou un pourcentage est affecté à chaque observation.
Application avec Excel
Vous retrouverez les données de cet exemple dans l’onglet MMP_donnees du fichier moyenne mobile.xlsx. Sa résolution se trouve dans l’onglet MMP_resultat.
Dans notre magasin de jouets, le comptable propose de réaliser une prévision selon la méthode des moyennes mobiles pondérées en utilisant un nombre N=2.
Il propose d’affecter un pourcentage de 40 % à l’observation la plus ancienne et un pourcentage de 60 % à l’observation la plus récente pour chaque moyenne mobile.
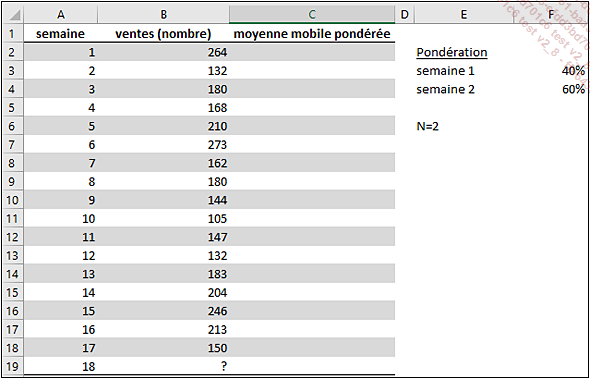
Dans la cellule C4, entrez la formule =B2*F$3+B3*F$4.
Copiez cette formule vers le bas en double cliquant sur la poignée de recopie de la cellule C4.
Le résultat est le suivant :
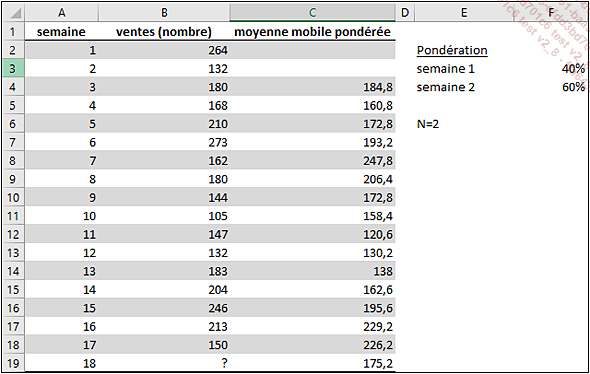
Et donc d’après ce modèle, pour la semaine 18, la prévision serait de 175 ordinateurs vendus.
Évaluation...
Le lissage exponentiel
Principe
L’idée derrière le lissage exponentiel est d’utiliser la dernière valeur connue corrigée de la différence entre cette dernière valeur et la dernière prévision.
Le lissage exponentiel est en quelque sorte un modèle qui s’autocorrige.
L’invention du lissage exponentiel est attribuée au mathématicien Siméon Denis Poisson, connu notamment pour la loi de Poisson (théorie des probabilités).
Exemple :
Les ventes réelles du mois de juin sont de 258 094 €.
La prévision réalisée concernant les ventes du mois de juin était de 259 913 €.
Première étape : définition du coefficient de lissage
Le coefficient de lissage (ou paramètre de lissage) est un nombre compris entre 0 et 1 ou entre 0 % et 100 %. Ce coefficient va représenter l’importance de l’autocorrection des erreurs dans le modèle.
Dans cet exemple, nous allons utiliser arbitrairement un coefficient de lissage de 30 %, nous verrons par la suite comment déterminer le coefficient de lissage le plus adéquat.
Deuxième étape : déterminer l’erreur entre les ventes réelles de la dernière observation connue et la dernière prévision réalisée en juin
Erreur réalisée juin = 258 094 - 259 913 = - 1 819
Troisième étape : appliquer le coefficient de lissage à l’erreur observée pour obtenir l’erreur pondérée de juin
Erreur pondérée juin = -1 819 x 0,3 = - 545,7
Quatrième étape : additionner l’erreur pondérée à la dernière prévision connue pour obtenir la nouvelle prévision pour le mois de juillet
Prévision juillet = 259 913 + (- 545,7) = 259 367,30
L’équation peut s’écrire :
Prévision juillet = prévision juin + 0,3(ventes réelles juin - prévision juin)
Ou encore
Prévision juillet = 0,7 x prévisions juin + 0,3 x ventes réelles juin
C’est cette dernière formule qui est utilisée par l’utilitaire d’analyse d’Excel.
Application avec Excel
Vous...
Travailler avec des saisonnalités
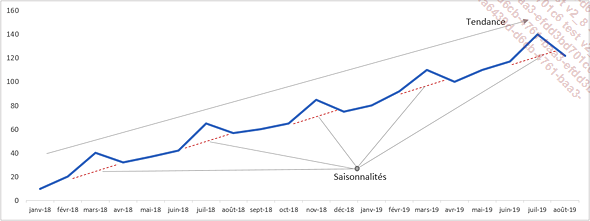
Selon l’activité de l’entreprise, il est possible d’observer des mouvements saisonniers, c’est-à-dire graphiquement des « pics et des creux » avec une amplitude plus ou moins régulière.
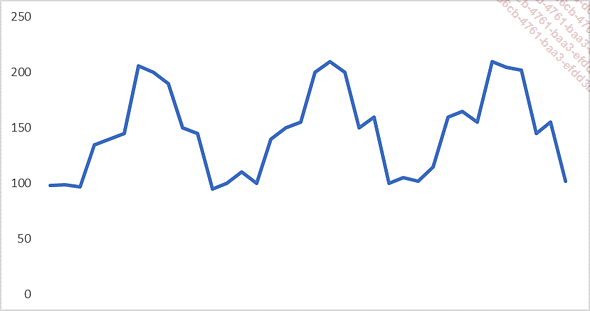
Il est aussi possible que la série chronologique ait à la fois une saisonnalité et une tendance.
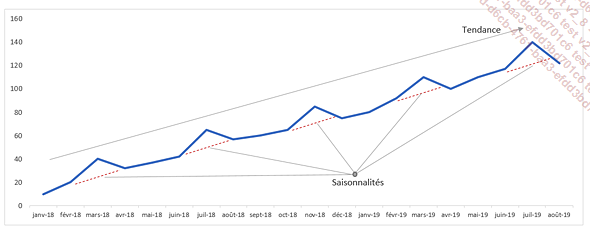
Les séries temporelles comportant une saisonnalité sont un peu plus difficiles à analyser.
Parfois, la saisonnalité masque la tendance générale de la série chronologique.
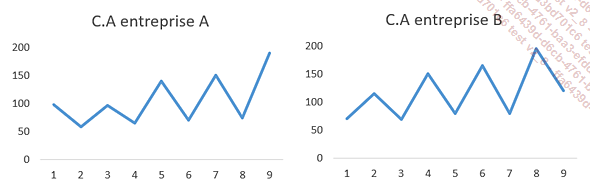
Si nous regardons l’évolution du chiffre d’affaires de l’entreprise A et de l’entreprise B, l’impression visuelle est que l’entreprise A est en pleine croissance alors que l’entreprise B est sur le déclin.
Ces deux entreprises sont a priori sujettes à des variations saisonnières, l’œil humain a tendance à juger sur la base de la dernière période. Or dans le cas de l’entreprise B, la période 9 est une saison basse, et il est bien possible que l’activité remonte à la période 10.
Nous allons voir différentes méthodes pour séparer la saisonnalité de la tendance, mesurer l’impact des saisonnalités sur l’activité et effectuer des prévisions sur une série chronologique comportant une saisonnalité.
Les coefficients saisonniers
Un coefficient saisonnier est le rapport d’une saison (ou de la moyenne d’une saison spécifique sur plusieurs années) par rapport à la moyenne d’une série.
Exemple
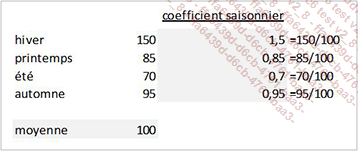
L’intérêt de ce calcul est double :
-
Établir une prévision des ressources nécessaires en fonction des fluctuations saisonnières de l’activité (recours à du travail intérimaire, heures supplémentaires, etc.).
-
Analyser la tendance en neutralisant les saisonnalités de la série chronologique. Pour cela, nous allons utiliser les coefficients saisonniers pour « désaisonnaliser » la série.
Exemple et application avec Excel
Imaginons que les entrées d’un parc zoologique se répartissent de la manière suivante entre 2017 et 2023 :...
Les nouvelles fonctions d’analyse des séries chronologiques
Depuis la version 2016 d’Excel, de nouveaux outils avancés permettant de réaliser des prévisions sont apparus.
Il s’agit des fonctions PREVISION.LINEAIRE, PREVISION.ETS, PREVISION.ETS.CARACTERESAISONNIER, PREVISION.ETS.CONFINT ainsi que l’outil Feuille de prévision.
La fonction PREVISION.ETS
La fonction PREVISION.ETS est basée sur un algorithme d’apprentissage de haut niveau et très efficace en matière de prévisions : le lissage exponentiel triple ou Exponential Triple Smoothing.
Cette méthode est aussi connue sous le nom de Holt - Winters, du nom des deux professeurs du MIT qui ont mis au point cet algorithme à partir de la méthode du lissage exponentiel.
Même si la démonstration mathématique du lissage exponentiel triple dépasse le cadre de cet ouvrage, dans le principe cette fonction estime à la fois :
-
la tendance de la série chronologique étudiée,
-
la composante saisonnière de la série chronologique étudiée (si elle existe),
-
l’algorithme du lissage exponentiel triple donne plus d’importance aux données récentes qu’aux données plus anciennes.
Application
À partir des données de l’onglet donnee_ETS du fichier nouv_fonc_prev.xlsx, nous allons effectuer une prévision du chiffre d’affaires pour les 15 prochains mois.
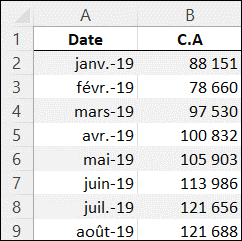
(8 premières lignes des données de l’onglet donnee_ETS)
La résolution de cet exemple se trouve dans l’onglet ETS.resolu du fichier nouv_fonc_prev.xlsx.
Visualisation de la série chronologique
Si nous réalisons un graphique en courbes à partir des données, nous obtenons ce graphique :
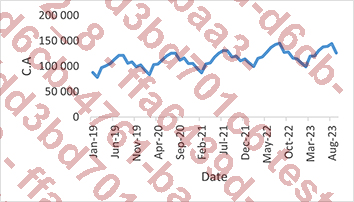
A priori, dans ce jeu de données, il existe une saisonnalité ainsi qu’une légère tendance positive.
Utilisation de la fonction PREVISION.ETS
Voyons ce que propose l’algorithme du lissage exponentiel triple avec la fonction PREVISION.ETS.
Dans la cellule A59 saisissez 01/10/2023.
Sélectionnez la cellule B59, saisissez =PREVISION.ETS( et
cliquez sur le bouton Insérer une fonction  situé dans la barre de formule.
situé dans la barre de formule.
La boîte de dialogue Argument de la fonction apparaît....
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations




