Décision, rentabilité et temporalité
Introduction
Ce chapitre consacré à la prise de décision aborde les trois éléments principaux à prendre en compte lors de l’estimation de la rentabilité d’un projet :
-
La prise en compte de la valeur temps.
L’étymologie du mot « finance » vient du latin « finire » : finir, mener à terme.
Ce sens ancien nous renseigne sur le but premier de la finance : avec le développement de la civilisation sont apparus à la fois l’échange à crédit et la mise en place de projets complexes entraînant un décalage temporel entre l’investissement initial et le retour sur investissement.
Nous aborderons dans cette partie différentes méthodes permettant d’estimer la rentabilité d’un projet en prenant en compte la temporalité.
-
L’optimisation des ressources en avenir certain.
Dans cette partie, nous étudierons deux méthodes pratiques d’optimisation avec Excel et l’outil Solveur.
-
La prise en compte de l’incertitude.
La décision d’investir ne peut s’effectuer qu’à partir du moment où l’espérance de gain l’emporte sur le risque associé au projet. Nous aborderons deux outils permettant de modéliser le risque : l’arbre de décision...
Le principe de capitalisation
Pour calculer la valeur future d’une somme, nous effectuons un calcul dit de capitalisation. Dans la vie courante, ce principe peut être illustré par les taux appliqués à l’épargne des particuliers :
Si nous plaçons 1 000 € sur un compte ayant un taux d’intérêt de 5 % par an, au bout d’un an nous aurons : 1 000 € x 1,05 = 1 050 €.
Au bout de deux ans, nous aurons : 1 000 € x 1,05 x 1,05 = 1 102,5 €
Il est aussi possible d’écrire 1 000 € x 1,05²
C’est ce que l’on appelle en finance la valeur capitalisée d’un flux.
La valeur capitalisée d’un flux unique peut se schématiser de la manière suivante :

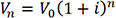
Avec
Vn : valeur à la période n
V0 : valeur à la période 0
i : taux d’intérêt
Valeur capitalisée d’une suite d’annuités constantes
Une annuité constante de placement est une somme d’argent versée à chaque période pour constituer par exemple une épargne.
Si nous prenons l’exemple d’un versement annuel de 1 000 € répété pendant trois ans au taux d’intérêt de 5 %, nous...
La valeur actuelle
La valeur actuelle est la situation inverse de la valeur capitalisée, cette fois, il s’agit de calculer la valeur actuelle d’une somme à percevoir dans le futur.

Exemple
Avec un taux d’intérêt de 5 %, quelle somme faudrait-il déposer pour atteindre un montant de 1 000 € au bout d’un an ?
1 000 € / 1,05 = 952,38 €
Ou
1 000 € x (1,05)-1 = 952,38 €
Dans ce cas, 952,38 € aujourd’hui est « économiquement équivalent » à 1 000 € dans 1 an.
Il est possible de vérifier ce calcul en calculant la valeur capitalisée de 952,38 € au taux d’intérêt de 5 % durant 1 an.
Nous avons :
952,38 € x (1,05) = 1 000 €
Toujours selon la même logique, combien d’épargne faudrait-il déposer pour arriver à la somme de 1 000 € dans deux ans ?
1 000 € / (1,05)2 = 907,03 €
Ou
1 000 € x (1,05)-2 = 907,03 €
C’est ce que l’on appelle en finance la valeur actualisée d’un flux.
Et nous pouvons écrire :
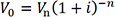 ou
ou 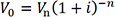
Avec
V0 : la valeur initiale
Vn : la valeur obtenue à la période n
n : le nombre de versements
i : le taux d’intérêt
Valeur...
La Valeur Actuelle Nette (VAN)
Principe
Évaluer un projet nécessite de comparer le capital investi à l’ensemble des flux de trésorerie estimés.
Cette comparaison implique l’évaluation du capital investi et des flux nets de trésorerie liés au projet à une même date. En général, cette date est le début du projet soit la date 0 et donc, le calcul de la VAN nécessite l’actualisation des flux de trésorerie estimés.
La VAN est la différence entre la prévision des flux nets de trésorerie actualisés relatifs à l’investissement et le coût initial lié à cet investissement.
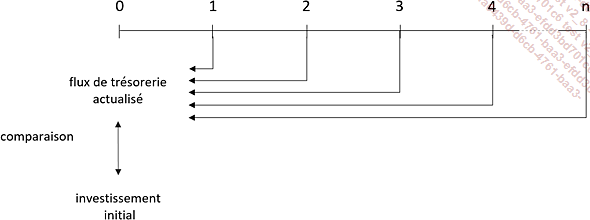
En anglais, le flux net de trésorerie est appelé cash-flow. Ce terme est aussi couramment utilisé en France.
Quelle est la signification du taux d’actualisation ?
Pour l’entreprise
L’actualisation des flux de trésorerie nécessite l’utilisation d’un taux d’actualisation. Pour l’entreprise, ce taux est le taux de rentabilité minimum exigé par l’entreprise.
En pratique, ce taux est équivalent au coût du capital utilisé par l’entreprise. Le capital dont dispose l’entreprise provient généralement de plusieurs sources. À chaque source correspond un coût.
Exemple : La banque prête à 5 %, les actionnaires demandent un dividende de 8 %, etc.
Le coût du capital est la moyenne pondérée des coûts des différentes sources de fonds auxquelles l’entreprise fait appel.
Si la VAN est positive, le projet est créateur de richesse pour l’entreprise.
À l’inverse, si la VAN est négative, le projet est destructeur de richesse pour l’entreprise. Il devrait donc a priori être rejeté.
Pour les investisseurs
Pour l’investisseur, le taux d’actualisation représente ce que l’on appelle le coût d’opportunité, c’est-à-dire le rendement d’un placement alternatif comportant un risque équivalent. L’investisseur pourra donc utiliser le taux du placement alternatif comme taux d’actualisation de la VAN du projet. Si la VAN calculée est positive, alors le projet est susceptible de générer...
Le taux interne de rentabilité (TIR)
Principe
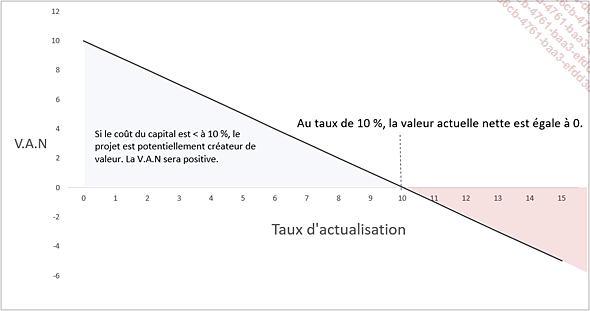
Le TIR est le taux pour lequel la VAN est nulle. Si ce taux est supérieur au taux d’actualisation retenu (en d’autres termes, au coût du capital), le projet est potentiellement créateur de valeur pour l’entreprise.
Cette méthode est peut-être la méthode la plus utilisée pour évaluer la rentabilité d’un projet.
Imaginons un projet ayant un coût de 100, susceptible de générer un cash-flow de 110 en N+1.
Nous avons :
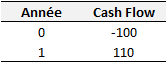
Le taux de rentabilité interne de ce projet est : (110 -100)/100 = 10 %
Au taux de 10 %, la VAN de ce projet est : - 100 + 110/(1,1) = 0
Le projet est potentiellement acceptable si le coût du capital de l’entreprise est inférieur à 10 %, car dans ce cas, la VAN du projet sera positive.
Imaginons à présent un projet ayant un coût initial de 100, un cash-flow de 0 en N+1 et un cash-flow de 110 en N+1.
Nous avons :
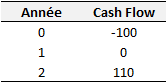
Nous pouvons écrire :
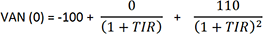
D’une manière générale, le TIR est la résolution de l’équation suivante :
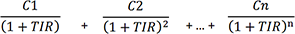
Exemple :
Un investissement de 32 000 € devrait engendrer un flux de trésorerie de 12 000 € dans un an, 14 400 € dans deux ans et 12 000 € dans trois ans.
Devons-nous accepter ce projet sachant que le coût du capital est estimé à 7 % ?
Nous avons l’équation suivante :
0 = - 32 000 + 12 000/(1+ TIR) + 14 400/(1 + TIR)^2 + 12 000/(1 + TIR)^3
TIR = 9,69 %
Le plus simple pour résoudre une telle équation est de faire plusieurs essais de taux de TIR successifs, mais bien entendu, Excel dispose d’une fonction qui calcule automatiquement le TIR.
Application avec Excel
Nous allons utiliser la formule TRI pour calculer le taux de rentabilité interne. À partir de l’exemple précédent, nous pouvons créer le tableau suivant :
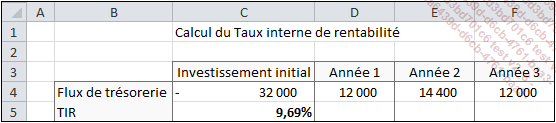
Vous retrouverez cet exemple dans l’onglet TIR du fichier VAN_tri.xlsx.
Le premier paramètre de la fonction TRI : les flux de trésorerie ; le deuxième paramètre (facultatif) est la valeur d’estimation....
Le délai de récupération du capital
Principe
Le délai de récupération indique la durée nécessaire pour que le cash-flow équilibre la dépense d’investissement initiale.
Le délai de récupération répond donc à la réponse suivante : combien de temps faut-il pour récupérer le capital investi ?
Il s’agit du critère de rentabilité des investissements le plus simple et le plus ancien, probablement aussi ancien que l’invention de la monnaie elle-même.
Exemple
Un investissement de - 1 000 permet d’avoir un cash-flow de 300 la première année, de 700 la deuxième année et de 2 000 la troisième année.
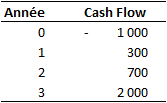
Délai de récupération : 2 ans (300 + 700 = 1 000)
Avec les éléments suivants :
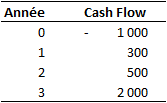
Année 1 : 300
Année 2 : 500
Année 3 : 2000
Capital restant = 1000 - 800 = 200
Fraction de la 3e année nécessaire à la récupération du capital :
200/2000 = 0,1
Délai de récupération = 2,1 années
Application avec Excel
Un investissement de 1 000 permettrait de dégager les cash-flows suivants :
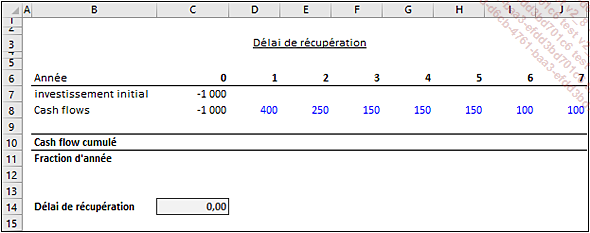
Vous retrouverez cet exemple dans l’onglet délai_recup_exercice du fichier delai_recup.xlsx. Sa résolution...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations




