La complexité des algorithmes
Présentation
Pour résoudre un problème donné, il est possible d’écrire différents algorithmes qui réalisent parfaitement le travail demandé. Néanmoins, il est possible que ces différents algorithmes n’aient pas les mêmes performances. Certains ont besoin de plus de temps ou de plus d’espace mémoire. La complexité algorithmique permet de les comparer de manière objective et sans se préoccuper du matériel utilisé.
La complexité en algorithmique comporte deux facettes. La première s’intéresse à la complexité minimale d’un problème donné (nommée théorie de la complexité) alors que la seconde s’intéresse aux algorithmes résolvant ce problème (nommé complexité des algorithmes). Cet ouvrage se concentre uniquement sur cette seconde facette.
Dans la plupart des cas, c’est la complexité en temps qui sera scrutée de près. Afin de calculer cette complexité, l’ensemble des opérations réalisées sont comptabilisées.
Il est possible de se concentrer uniquement sur les opérations fondamentales, c’est-à-dire les opérations les plus coûteuses, les autres étant estimées négligeables par rapport à celles-ci. Comme...
L’ordre de grandeur de la complexité
Le calcul exact n’est généralement pas nécessaire. L’ordinateur réalisant plusieurs milliards d’opérations par seconde, il n’est pas à quelques opérations près !
Soient les complexités de trois algorithmes :
Complexité(Algo1) = 3n + 3
Complexité(Algo2) = 7n - 5
Complexité(Algo3) = n² - 4 n - 7
Supposons que nous utilisons ces algorithmes avec des données ayant une taille n=10 puis 1 000 puis 1 000 000.

Avec des valeurs de n petites, le nombre d’opérations réalisées semble du même ordre de grandeur. Pour n=10, c’est de l’ordre de quelques dizaines d’opérations. Cependant, lorsque n devient plus grand, l’ordre de grandeur n’est plus le même pour les trois algorithmes. C’est d’ailleurs pour des données de grande taille en entrée que la complexité est un élément important à prendre en compte. Effectivement, pour des données de petites tailles, n’importe quel algorithme fait l’affaire. Pour n=1 000, l’ordre de grandeur des deux premiers algorithmes est du millier d’opérations alors que pour le troisième l’ordre de grandeur est du million d’opérations. Cela est encore plus visible avec n=1 000 000. Les deux premiers...
Les catégories de complexité
Avec les ordres de grandeur, il est possible de catégoriser les complexités des algorithmes dans les familles suivantes :
|
Complexité |
Nom |
Exemple |
|
Ο(1) |
Complexité constante |
Accès à une case précise d’un tableau |
|
Ο(log(n)) |
Complexité logarithmique |
Recherche d’une valeur dans un tableau trié (Recherche dichotomique) |
|
Ο(n) |
Complexité linéaire |
Recherche d’une valeur dans un tableau non trié |
|
Ο(n log(n)) |
Complexité linéarithmique |
Tri d’un tableau (Tri par tas) |
|
Ο(n²) |
Complexité quadratique (cas particulier d’une complexité polynomiale) |
Tri d’un tableau avec un algorithme naïf (Tri par sélection) |
|
Ο(n3) |
Complexité cubique (cas particulier d’une complexité polynomiale) |
Multiplication matricielle naïve |
|
Ο(2n) |
Complexité exponentielle |
Problème du sac à dos par brute force |
|
Ο(n!) |
Complexité factorielle |
Problème du voyageur de commerce par une approche naïve |
En traçant les courbes des fonctions associées à ces ordres de grandeur, il est assez aisé de se rendre compte de la différence entre elles lorsque la valeur de n devient grande.
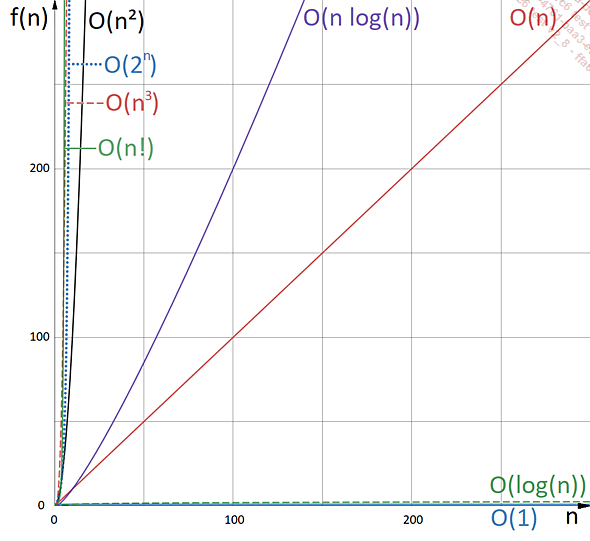
Les algorithmes avec une complexité constante (Ο(1)) ou logarithmique (Ο(log(n)))...
Illustration avec les algorithmes de tri
Les algorithmes de tri de valeurs parmi un ensemble de données sont de bons exemples pour illustrer les différentes complexités. Dans cet ouvrage, les algorithmes sont réalisés pour trier par ordre croissant un tableau de valeurs réelles, mais il est possible de les adapter pour d’autres types de données ordonnées ou pour trier dans un ordre décroissant.
Afin de pouvoir comparer les différents algorithmes de tri, ceux-ci sont tous présentés sous la même forme. Il s’agit d’une classe implémentant une interface ayant deux méthodes :
-
Une fonction retournant le nom de l’algorithme.
-
Une procédure prenant en paramètre le tableau à trier ainsi que sa taille.
Interface Trieur
Fonction abstraite getNom() Retourne texte
Procédure abstraite trier(tableau : réel[], taille : entier)
FInterface L’algorithme suivant permet d’essayer les différents algorithmes de tri présentés dans les lignes suivantes :
Constante TAILLE : entier <- 10
Algo Tri
Variable algosDeTri : Trieur[7]
Variable t : réel[]
Variable i, numAlgo : entier
Début
algosDeTri[0] <- nouveau TriSelection()
algosDeTri[1] <- nouveau TriBulles()
algosDeTri[2] <- nouveau TriInsertion()
algosDeTri[3] <- nouveau TriShell()
algosDeTri[4] <- nouveau TriFusion()
algosDeTri[5] <- nouveau TriRapide()
algosDeTri[6] <- nouveau TriParTas()
écrire("Quel algorithme de tri souhaitez-vous utiliser ?")
Pour i <- 0 à 6
écrire(i+1 & " - " & algosDeTri[i].getNom())
FPour
numAlgo <- saisir()-1
t <- genererTabAlea()
afficher(t)
écrire("tri avec l'algorithme " & algosDeTri[numAlgo].getNom())
algosDeTri[numAlgo].trier(t...Exercices
1. L’ordre de grandeur
Donner l’ordre de grandeur et le nom de la catégorie de complexité d’algorithmes ayant les complexités suivantes :
-
Complexité(A) = 2n² + 7n + 24
-
Complexité(B) = 4n + 3n log(n) + n²
-
Complexité(C) = 7n + 3n log(n) - 2
-
Complexité(D) = 7n + log(n) - 7
2. L’implémentation des algorithmes de tri en Java
Implémenter l’un des algorithmes de tri en Java. Tester ensuite cet algorithme avec plusieurs tableaux de valeurs tirées aléatoirement et vérifier automatiquement que le tableau est bien trié après l’appel à la méthode de tri.
Solutions des exercices
1. L’ordre de grandeur
-
Complexité(A) = 2n² + 7n + 24
Suppression des coefficients multiplicateurs :
n² + n + 24
Suppression des ajouts ou des soustractions de valeurs constantes :
n² + n
Suppression des termes qui ne sont pas dominants :
n²
Complexité(A) = O(n²)
L’algorithme A a une complexité quadratique.
-
Complexité(B) = 4n + 3n log(n) + n²
Suppression des coefficients multiplicateurs :
n + n log(n) + n²
Suppression des ajouts ou des soustractions de valeurs constantes :
n + n log(n) + n²
Suppression des termes qui ne sont pas dominants :
n²
L’algorithme B a une complexité quadratique.
-
Complexité(C) = 7n + 3n log(n) - 2
Suppression des coefficients multiplicateurs :
n + n log(n) - 2
Suppression des ajouts ou des soustractions de valeurs constantes :
n + n log(n)
Suppression des termes qui ne sont pas dominants :
n log(n)
L’algorithme C a une complexité linéarithmique.
-
Complexité(D) = 7n + log(n) - 7
Suppression des coefficients multiplicateurs :
n + log(n) - 7
Suppression des ajouts ou des soustractions de valeurs constantes :
n + log(n)
Suppression des termes qui ne sont pas dominants :
n
L’algorithme D a une complexité linéaire.
2. L’implémentation des algorithmes de tri en Java
package fr.eni.chapitre13.exercice2;
import java.util.Random;
import java.util.Scanner;
import fr.eni.chapitre13.*;
public class Tri {
private static Scanner console = new Scanner(System.in);
private static Random rand = new Random();
public static final int TAILLE = 10;
public static final int NB_REPET = 10;
public static void main(String[] args) {
Trieur[] algosDeTri = new Trieur[7];
double[] t = new double[TAILLE];
int i, numAlgo;
algosDeTri[0] = new TriSelection();
algosDeTri[1] = new TriBulles();
algosDeTri[2] = new TriInsertion();
algosDeTri[3] = new TriShell(); ... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

