Les tableaux
Présentation
Avec les connaissances acquises avec la lecture des chapitres précédents, il n’est possible de mettre qu’une seule valeur dans une variable. Mais cela va changer grâce aux tableaux.
Attention, si vous avez déjà vu la notion de tableau dans des langages de programmation tels que JavaScript, PHP ou Python par exemple, méfiez-vous, car ces langages utilisent en réalité des tableaux associatifs, qui sont des structures de données différentes des tableaux présentés dans ce chapitre.
Un tableau est donc une sorte particulière de variable capable de stocker un ensemble de valeurs, toutes de même type. Ces valeurs sont positionnées dans ce qui se nomme les cases du tableau. Afin de pouvoir s’y retrouver dans toutes ces cases, celles-ci sont numérotées par un nombre entier appelé indice.
Il est possible de faire l’analogie avec une rue ayant plusieurs maisons. Pour se retrouver parmi cet ensemble de maisons, elles possèdent chacune un numéro différent dans leur adresse. Ce numéro dans la rue correspond à l’indice pour les cases de notre tableau.
Voici un exemple de tableau à 5 cases contenant chacune une valeur entière :
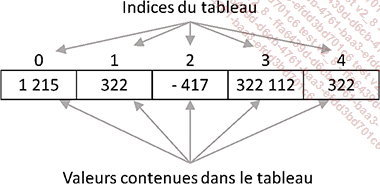
Les indices sont numérotés à partir de zéro. Ainsi la première case du tableau est à l’indice...
La déclaration d’un tableau
Les tableaux sont des variables particulières puisqu’ils sont capables de stocker plusieurs valeurs, mais ce sont tout de même des variables. Il faut donc les déclarer dans la section de déclaration comme les autres variables. Voici la syntaxe permettant la déclaration d’un tableau :
Variable nomDuTableau : type[tailleDuTableau] La déclaration est assez similaire à la déclaration des autres variables. Cette déclaration commence également par le mot-clé Variable suivi du nom choisi pour le tableau. Après le caractère deux-points est indiqué le type de valeur qui sera stocké dans les cases du tableau (n’oubliez pas que les valeurs contenues dans chaque case du tableau doivent toutes être du même type). Enfin, c’est là toute la différence, entre crochets est indiquée la taille du tableau, c’est-à-dire le nombre de cases que doit contenir ce tableau.
Exemples :
# déclaration d'un tableau de dix entiers :
Variable te : entier[10]
# déclaration d'un tableau de 3 nombres réels :
Variable tr : réel[3]
# déclaration d'un tableau de 30 caractères :
Variable tc : caractère[30]
# déclaration d'un tableau...L’utilisation d’un tableau
Pour accéder à l’une des cases du tableau, il faut préciser laquelle parmi l’ensemble des cases du tableau. C’est grâce à l’indice de la case que cela est indiqué. Par exemple, pour indiquer la case d’indice trois du tableau (c’est-à-dire la quatrième case du tableau), il faut indiquer nomDuTableau[3]. Une fois qu’une des cases du tableau a été spécifiée, il est possible de réaliser les mêmes opérations que s’il s’agissait d’une simple variable. Il est par exemple possible de stocker une valeur dedans : nomDuTableau[3] <- 22 ou d’afficher sa valeur : écrire(nomDuTableau[3]).

Attention lorsque vous précisez l’indice pour accéder à une case du tableau que cet indice ait une valeur acceptable, c’est-à-dire que sa valeur soit comprise entre zéro et la taille du tableau moins un.
Voici un exemple d’algorithme utilisant un tableau :
Algo Tableaux
Variable tab : réel[3]
Début
tab[0] <- 1,61803398875
tab[1] <- 2,71828182846
tab[2] <- 3,14159265359
écrire("nombre d'or = " & tab[0])
écrire("e = " & tab[1])
écrire("pi = " &...Le parcours d’un tableau
Il est assez courant d’avoir à répéter une opération sur l’ensemble des cases du tableau. Pour cela, une boucle Pour est utilisée et la valeur de la variable de cette boucle est utilisée comme valeur d’indice pour accéder à chaque case du tableau.
Exemple :
Algo Tableaux2
Constante TAILLE : entier <- 10
Variable tab : entier[TAILLE]
Variable i : entier
Début
Pour i <- 0 à TAILLE - 1
tab[i] <- i + 1
FPour
Fin Lors de la première itération de la boucle, la variable i vaut zéro donc tab[i] permet d’accéder à la case d’indice zéro du tableau, c’est-à-dire la première case du tableau. Celle-ci est initialisée avec la valeur un (i+1). Lors de la deuxième itération, la variable i vaut un donc tab[i] correspond à tab[1] et cette deuxième case est initialisée à la valeur deux. Ainsi de suite, jusqu’à ce que la dernière case du tableau, la case d’indice neuf, soit initialisée avec la valeur dix. Ainsi, les cases du tableau ont été initialisées de la manière suivante :

Cette boucle Pour se traduit par une boucle for en Java. Cela donne par exemple :
final int TAILLE = 10;
int[] tab = new int[TAILLE];
for (int i = 0; i < TAILLE; i++) {
tab[i] = i+1;
} En Java, il est possible de se passer de la constante TAILLE, car la taille d’un tableau est directement intégrée dans le tableau. Pour cela, il faut avoir recours à :
nomDuTableau.length Ce qui permet de simplifier le code précédent en ceci :
int[] tab = new int[10];
for (int i = 0; i < tab.length; i++) {
tab[i] = i+1;
} En Java, il existe une quatrième boucle qui n’a pas d’équivalent en algorithmique. Il s’agit de la boucle foreach, c’est-à-dire "pour chaque". Bien qu’elle se nomme foreach, elle s’écrit avec le mot-clé for par souci d’économie de mot-clé. Mais la syntaxe suivante permet de bien la distinguer d’une boucle for classique :...
Les tableaux : un type référence
Comme nous l’avons vu précédemment, les tableaux contiennent plusieurs valeurs. Pour des raisons d’optimisation, ils ne sont pas traités comme les variables vues précédemment. Celles-ci sont des types valeur alors que les tableaux sont des types référence. Cette différence est expliquée en détail dans le chapitre La mémoire. Néanmoins, pour le moment, il faut retenir que lorsqu’une affectation est effectuée pour un tableau cela ne produit pas une copie du tableau, mais les deux variables de type tableau référencent les mêmes cases du tableau. Une modification par l’une ou l’autre des variables de type tableau modifie le même tableau. Ce n’est donc pas le tableau qui a été dupliqué, mais le moyen d’y accéder qui a été dupliqué.
L’algorithme suivant illustre cela :
Algo TableauTypeReference
Constante TAILLE : entier <- 4
Variable t1 : entier[TAILLE]
Variable t2 : entier[]
Variable i : entier
Début
Pour i <- 0 à TAILLE - 1
t1[i] <- i + 1
FPour
t2 <- t1
t2[2] <- 9
t1[0] <- 6
Pour i <- 0 à TAILLE - 1
écrire("t1[" & i & "] = " & t1[i] & "...Les tableaux multidimensionnels
Il est possible de déclarer un tableau à plusieurs dimensions. Voici par exemple un tableau à deux dimensions :
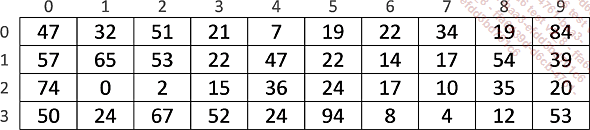
Afin de créer un tableau multidimensionnel, il faut déclarer un tableau de la même manière que précédemment, mais il faut en plus rajouter la taille pour les dimensions supplémentaires.
Syntaxe :
Variable nomDuTableau :
type[dimension1][dimension2]...[dimensionN] Une question se pose : pour créer un tableau d’entiers avec quatre lignes et dix colonnes, faut-il déclarer Variable tab2d : entier[4][10] ou Variable tab2d : entier[10][4] ? En fait, les deux façons de faire sont possibles : dans la mémoire, les valeurs ne sont pas organisées de cette manière-là. Par contre, une fois que ce choix a été effectué, il faudra être cohérent : si la première dimension correspond aux lignes et la seconde aux colonnes, il faut que par la suite ce soit toujours le cas. Dans cet ouvrage, c’est ce choix qui est fait. Ainsi, pour déclarer ce tableau, il faut indiquer :
Variable tab2d : entier[4][10] Il n’y a pas de limite au nombre de dimensions : il est possible de réaliser un tableau à dix dimensions si vous le souhaitez mais généralement, il est assez difficile de s’y retrouver dans toutes ces dimensions alors que nous vivons dans un monde qui ne possède que trois dimensions. C’est pourquoi dans cet ouvrage nous nous limiterons à deux dimensions. Cela est suffisant pour que vous compreniez le concept.
Pour accéder à une case d’un tableau multidimensionnel, il ne faut plus préciser qu’un seul indice, mais autant d’indices qu’il y a de dimensions. Ainsi une et une seule case est désignée. Par exemple pour accéder à la case de la troisième ligne et de la septième colonne du tableau précédent, il faut indiquer tab2d[2][6]. Une fois précisée une case déterminée du tableau, il est possible de la manipuler comme si nous avions affaire...
Exercices
1. Décollage immédiat
Écrire un algorithme inscrivant les valeurs comprises entre dix et zéro par ordre décroissant dans un tableau, puis qui parcourt ce tableau pour afficher le compte à rebours.
2. Nombres d’occurrences
Réaliser un algorithme qui fait saisir à l’utilisateur autant de chiffres compris entre zéro et neuf qu’il souhaite. Une fois que l’utilisateur a mis fin à sa série en saisissant -1, l’algorithme affiche le nombre de fois que chaque chiffre a été saisi.
Exemple d’exécution :
|
Entrer une valeur comprise entre 0 et 9 ou -1 pour finir... : |
|
2 |
|
Autre valeur, svp ou -1 pour finir... |
|
9 |
|
Autre valeur, svp ou -1 pour finir... |
|
2 |
|
Autre valeur, svp ou -1 pour finir... |
|
2 |
|
Autre valeur, svp ou -1 pour finir... |
|
0 |
|
Autre valeur, svp ou -1 pour finir... |
|
-1 |
|
Nombre de 0 : 1 |
|
Nombre de 1 : 0 |
|
Nombre de 2 : 3 |
|
Nombre de 3 : 0 |
|
Nombre de 4 : 0 |
|
Nombre de 5 : 0 |
|
Nombre de 6 : 0 |
|
Nombre de 7 : 0 |
|
Nombre de 8 : 0 |
|
Nombre de 9 : 1 |
3. Moyenne de notes (version 4)
Produire un algorithme saisissant des notes dans un tableau. À la fin de la saisie, il affiche l’ensemble des notes et leur moyenne.
Exemple d’exécution de l’algorithme :
|
Note ? |
|
12 |
|
Note ? |
|
15 |
|
Note ? |
|
8 |
|
Note ? |
|
7 |
|
Note ? |
|
-1 |
|
La moyenne des notes (12; 15; 8; 7) est de 10,5. |
4. Machine à voter
Réaliser un algorithme qui demande aux utilisateurs de voter (les utilisateurs vont se relayer pour utiliser chacun leur tour votre machine à voter). Plusieurs candidats sont proposés. À la fin de la journée, le président du bureau de vote entre un code particulier pour mettre fin au vote (68753421) et les résultats sont affichés. Bien entendu, cet exercice est théorique puisque la sécurité n’est pas du tout assurée et qu’un utilisateur peut voter plusieurs fois…
Exemple d’exécution de l’algorithme :
|
Choisissez parmi : |
|
1 - Émilie FRELAND |
|
2 - Gérard BOUCHARD |
|
3 - Marie JUSTEAU |
|
4 - Nadia LETORD |
|
4 |
|
a voté ! |
|
Choisissez parmi : |
|
1 - Émilie FRELAND |
|
2 - Gérard BOUCHARD |
|
3 - Marie JUSTEAU |
|
4 - Nadia LETORD |
|
1 |
|
a voté ! |
|
Choisissez parmi : |
|
1 - Émilie FRELAND |
|
2 - Gérard BOUCHARD |
|
3 - Marie JUSTEAU |
|
4 - Nadia LETORD |
|
3 |
|
a voté ! |
|
Choisissez parmi : |
|
1 - Émilie FRELAND |
|
2 - Gérard... |
Solutions des exercices
1. Décollage immédiat
Algo Decollage
# inscrit les valeurs comprises entre dix et zéro par ordre
# décroissant dans un tableau puis parcourt ce tableau pour
# afficher le compte à rebours.
Constante TAILLE : entier <- 11
Variable cptR : entier[TAILLE]
Variable i : entier
Début
# remplissage du tableau
Pour i <- 0 à TAILLE - 1
cptR[i] <- TAILLE - 1 - i
FPour
# affichage des valeurs contenues dans le tableau
Pour i <- 0 à TAILLE - 1
écrire(cptR[i])
FPour
Fin 2. Nombres d’occurrences
Algo NbOcc
# Saisit des chiffres et calcule le nombre d'occurrences de chacun
Constante TAILLE : entier <- 10
Constante STOP : entier <- -1
Variable tab : entier[TAILLE]
Variable i, valeur : entier
Début
# Initialisation du tableau
Pour i <- 0 à TAILLE-1
tab[i] <- 0
FPour
# Saisie des valeurs
valeur <- saisir("Entrer une valeur comprise entre" &
" 0 et " & TAILLE-1 & " ou " & STOP &" pour finir : ")
TantQue valeur ≠ STOP
Si valeur < 0 ou valeur >= TAILLE Alors
écrire("N'est pas une valeur entre 0" &
" et " & TAILLE-1 & " !")
Sinon
tab[valeur] <- tab[valeur] + 1
FSi
valeur <- saisir("Autre valeur, svp ou " & STOP &" pour finir : ")
FTq
# Affichage des résultats
Pour i <- 0 à TAILLE-1
écrire("Nombre de " & i & " : " & tab[i])
FPour
Fin 3. Moyenne de notes (version 4)
Algo MoyenneDesNotesV4
# Calcule la moyenne des notes saisies par l'utilisateur (il saisit
# -1 pour finir la saisie). Les notes sont stockées dans un tableau.
Constante TAILLE : entier <- 100
Constante STOP : entier <- -1
Variable notes : réel[TAILLE]
Variable nbVal : entier <- 0
Variable saisie : réel
Variable i : entier
Variable total : réel
Début
saisie <- saisir("Note ? ")
TantQue saisie ≠ STOP et nbVal < TAILLE
notes[nbVal] <- saisie
nbVal <- nbVal + 1
saisie <- saisir("Note ? ")
FTq
# Si c'est l'utilisateur qui a clos la saisie
Si saisie = STOP Alors
Si nbVal ≠ 0 Alors
écrireSRC("La moyenne des notes (" & notes[0])
total <- notes[0]
Pour i <- 1 à nbVal-1
total <- total + notes[i]
écrireSRC("; " & notes[i])
FPour
écrire(") est de " & total/nbVal)
Sinon
écrire("Aucune note n'a été saisie")
FSi
Sinon
écrire("La capacité du tableau a été dépassée, désolé")
FSi
Fin 4. Machine à voter
Algo MachineAVoter
# Simule une machine à voter simplifiée
Constante FIN : entier <- 68753421
Constante NB_CAND : entier <- 4
Variable votes : entier[NB_CAND]
Variable candidats : texte[NB_CAND]
Variable saisie, i : entier
Variable nbVotes : entier <- 0
Début
# initialisation
Pour i <- 0 à NB_CAND - 1
votes[i] <- 0
FPour
candidats[0] <- "Émilie FRELAND"
candidats[1] <- "Gérard BOUCHARD"
candidats[2] <- "Marie JUSTEAU"
candidats[3] <- "Nadia LETORD"
# votes
Répéter
écrire("Choisissez parmi :")
Pour i <- 0 à NB_CAND - 1
écrire(i+1 & " - " & candidats[i])
FPour
saisie <- saisir()
Si saisie ≠ FIN Alors
Si saisie > 0 et saisie ≤ NB_CAND Alors
votes[saisie - 1] <- votes[saisie - 1] +1
écrire("a voté !")
nbVotes <- nbVotes + 1
Sinon
écrire("Vote nul !")
FSi
FSi
TantQue saisie ≠ FIN FRépéter
# affichage des résultats
écrire("Résultats :")
Pour i <- 0 à NB_CAND - 1
écrire (candidats[i] & " : " & votes[i] * 100 / nbVotes & "%")
FPour
Fin 5. Palindrome
Algo Palindrome
# Saisit un mot et indique s'il s'agit d'un palindrome
Constante TAILLE : entier <- 30
Constante STOP : caractère <- '#'
Variable mot : caractère[TAILLE]
Variable nbCar : entier <- 0
Variable palin : booléen <- VRAI
Variable i : entier
Début
#### Saisie du mot ####
écrire("Entrez un mot puis tapez " & STOP)
Répéter
mot[nbCar] <- saisir()
Si mot[nbCar] ≠ STOP Alors
Si mot[nbCar] < 'a' ou mot[nbCar] > 'z' Alors
écrire("Ce caractère n'est pas autorisé, il ne faut" &
"écrire que des lettres minuscules sans accent ni cédille")
Pour i <- 0 à nbCar-1 # Réécriture du début du mot
écrireSRC(mot[i])
FPour
Sinon
nbCar <- nbCar + 1
FSi
FSi
TantQue mot[nbCar] ≠ STOP FRépéter
i <- 0
#### Test du mot pour voir si c'est un palindrome ####
TantQue palin et i<nbCar div 2
palin <- mot[i]=mot[nbCar-1-i]
i <- i+1
FTq
écrireSRC("Le mot ")
Pour i <- 0 à nbCar-1
écrireSRC(mot[i])
FPour
Si palin Alors
écrire(" est un palindrome")
Sinon
écrire(" n'est pas un palindrome")
FSi
Fin 6. Que fait-il donc ?
-
Numérote toutes les cases du tableau de 1 à TAILLE×TAILLE ligne par ligne.
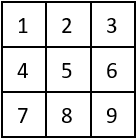
-
Deuxième version :
Algo QueFaitIlDoncV2
# Numérote toutes les cases du tableau de 1 à TAILLE×TAILLE
# colonne par colonne
Constante TAILLE : entier <- 4
Variable i, j, val : entier
Variable tab2d : entier[TAILLE][TAILLE]
Début
val <- 1
Pour j <- 0 à TAILLE - 1
Pour i <- 0 à TAILLE - 1
tab2d[i][j] <- val
val <- val + 1
FPour
FPour
Fin -
Troisième version :
Algo QueFaitIlDoncV3
# Remplit toutes les cases du tableau avec la distance au coin
# en haut à gauche
Constante TAILLE : entier <- 4
Variable i, j : entier
Variable tab2d : entier[TAILLE][TAILLE]
Début
Pour j <- 0 à TAILLE - 1
Pour i <- 0 à TAILLE - 1
tab2d[j][i] <- i + j
FPour
FPour
Fin 7. Matrix
Algo EnterIntoTheMatrix
# Affiche une matrice remplie de caractères aléatoires
Constante HAUTEUR : entier <- 20
Constante LARGEUR : entier <- 30
Variable i, j : entier
Variable matrix : caractère[HAUTEUR][LARGEUR]
Début
Pour j <- 0 à HAUTEUR - 1
Pour i <- 0 à LARGEUR - 1
matrix[j][i] <- aléa(' ', '²')
FPour
FPour
Pour j <- 0 à HAUTEUR - 1
Pour i <- 0 à LARGEUR - 1
écrireSRC(matrix[j][i])
FPour
écrire()
FPour
Fin 8. Micro bataille navale
Algo MicroBatailleNavale
# Jeu de la Bataille Navale avec un seul bateau d'une case
Constante HAUTEUR : entier <- 4
Constante LARGEUR : entier <- 4
Constante PLOUF : caractère <- '~'
Constante BATEAU : caractère <- 'b'
Constante EAU : caractère <- 'e'
Variable plateau : caractère[HAUTEUR][LARGEUR]
Variable i, j : entier
Début
# Initialisation du plateau de jeu
Pour j <- 0 à HAUTEUR-1
Pour i <- 0 à LARGEUR-1
plateau[j][i] <- EAU
FPour
FPour
# Dépôt d'un bateau d'une case sur une case choisie aléatoirement
i <- aléa(0, HAUTEUR-1)
j <- aléa(0, LARGEUR-1)
plateau[i][j] <- BATEAU
Répéter
Pour j <- 0 à HAUTEUR-1 # Affichage du plateau de jeu
Pour i <- 0 à LARGEUR-1
Si plateau[j][i] = BATEAU ou plateau[j][i] = EAU Alors
écrireSRC("?")
Sinon
écrireSRC(plateau[j][i])
FSi
FPour
écrire()
FPour
Répéter
# Saisie des coordonnées de tir
i <- saisir("Quelle colonne (entre 1 et "&LARGEUR&") : ")-1
j <- saisir("Quelle ligne (entre 1 et "&HAUTEUR&") : ")-1
TantQue i < 0 ou i ≥ LARGEUR ou j < 0 ou j ≥ HAUTEUR FRépéter
Si plateau[j][i] ≠ BATEAU Alors # test du tir
plateau[j][i] <- PLOUF
écrire("Plouf ! ")
FSi
TantQue plateau[j][i] ≠ BATEAU FRépéter
écrire("Touché Coulé ! Bravo, vous avez gagné !")
Fin 9. Morpion
Algo Morpion
Constante SYMBOLE1 : caractère <- 'O'
Constante SYMBOLE2 : caractère <- 'X'
Constante INDEFINI : caractère <- 'I'
Constante VIDE : caractère <- ' '
Variable grille : caractère[3][3]
Variable nbCoupsJoues : entier <- 0
Variable joueur : caractère <- SYMBOLE1
Variable gagnant : caractère <- INDEFINI
Variable l, c : entier
Début
#initialisation de la grille
Pour l <- 0 à 2
Pour c <- 0 à 2
grille[l][c] <- VIDE
FPour
FPour
Répéter #boucle de jeu
#affichage de la grille de jeu
Pour l <- 0 à 2
Pour c <- 0 à 2
écrireSRC(grille[l][c])
FPour
écrire()
FPour
écrire("C'est au joueur " & joueur & " de jouer")
l <- saisir("ligne : ")
c <- saisir("colonne : ") ... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

