La mémoire

1. Les nombres entiers

1. Les octets

2. Les entiers naturels

Les entiers naturels sont les nombres entiers positifs ou nuls, c’est-à-dire ceux trouvables dans la nature : il peut y avoir deux arbres, un arbre, aucun arbre, c’est-à-dire zéro, mais il ne peut pas y avoir -2 arbres !

Pour coder ces valeurs, les ordinateurs utilisent directement la valeur en base deux codée avec le nombre d’octets souhaité....

1. La forme normalisée

En base dix, un nombre réel peut être représenté sous sa notation scientifique. Cela consiste à transformer la valeur afin qu’elle soit de la forme suivante :

±m × 10^exp

où ± correspond au signe et m est une valeur comprise entre un (compris) et dix (non compris). La valeur m s’appelle la mantisse. Afin que la mantisse soit comprise dans cet intervalle, il est nécessaire de décaler la virgule. Ainsi, le décalage de la virgule vers la gauche de n positions oblige à ajouter une multiplication par dix puissance n pour conserver la même valeur. Un décalage de n positions vers la droite nécessite l’ajout d’une multiplication par dix puissance -n.

Exemple :

En base deux, il est également possible de mettre un nombre sous sa notation scientifique. Celle-ci est appelée forme normale. Il est nécessaire que la mantisse soit de la forme 1,…

Exemple :

2. La norme IEEE-754

Cette norme définit la représentation utilisée par les ordinateurs pour les nombres réels. Les valeurs mises sous leur forme normale possèdent trois informations : le signe, la mantisse et l’exposant. Ce sont ces trois informations qui sont stockées en mémoire.

Exemple :

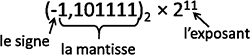
La norme IEEE 754 propose différents formats, dont deux sont utilisés en Java comme dans la plupart des langages de programmation :

Dans le cas de la simple précision...

1. Le code ASCII

La table ASCII (American Standard Code for Information Interchange) a été créée à cet effet. Ainsi, les caractères utilisés par les Américains ont été positionnés dans cette table afin d’avoir un encodage pour ceux-ci.

Voici la table ASCII :

Pour connaître l’encodage utilisé pour un caractère, il faut additionner la valeur de la ligne avec la valeur de la colonne. Par exemple, pour le caractère M, il faut additionner la valeur 40 avec la valeur 0D. Ainsi, le caractère M est codé 4D en ASCII. La valeur obtenue est directement en hexadécimal, ce qui simplifie le travail !

À l’observation de cette table, plusieurs éléments sont à remarquer. Tout d’abord, les deux premières lignes peuvent sembler étranges puisqu’elles ne sont pas réellement des caractères, mais des caractères de contrôle (retour à la ligne, sonnerie, retour arrière…).

Ensuite la troisième ligne commence par le caractère espace, suivi de caractères spéciaux (caractères de ponctuation et caractères mathématiques). La quatrième ligne contient les dix chiffres, suivis d’autres caractères spéciaux. Les cinquième et sixième lignes contiennent les lettres majuscules dans l’ordre de l’alphabet et d’autres caractères spéciaux. Il en est de même pour les deux dernières lignes pour les lettres minuscules de l’alphabet. Enfin, il est à noter qu’il n’y a pas les caractères accentués, le c avec cédille et les caractères entrelacés (œ et æ). L’ASCII n’a été...

1. La pile

Les variables de type valeur (boolean, byte, short, int, long, char, float et double) sont stockées directement sur la pile. Les valeurs sont stockées les unes à la suite des autres dans l’ordre dans lequel elles ont été déclarées. Lorsqu’un bloc se termine, les variables qui ont été déclarées à l’intérieur de celui-ci sont détruites. Plus précisément, l’espace est considéré comme disponible et, lors de l’écriture des prochaines variables, leur valeur est écrasée. Les variables sont ainsi "empilées" et "dépilées" au fil des créations de variables et des fins de blocs. C’est pour cette raison que cette partie de la mémoire s’appelle la pile.

Exemple :

private static void testVariablesEtBlocs() { 
   // 1 
   char car; 
   // 2 
   int a = 27897; 
   // 3 
   if(a<Math.sqrt(Integer.MAX_VALUE)) { 
       int c = a*a; 
       // 4 
       System.out.printf("le carré de %d est %d%n", a, c); 
   } 
   // 5 
   car = 'H'; 
   final int TABLE = 4; 
   // 6 
   System.out.printf("table de %d :%n", TABLE); 
   for (int i = 1; i < 10; i++) { 
       int res = i*TABLE; 
       // 7 
       System.out.printf("%d × %d = %d%n", i, TABLE, res); 
   } 
   //8 
   System.out.println("car = " + car); 
}...

1. Conversion d’une base à une autre

b. Convertir les valeurs suivantes en base 2 et en base 16

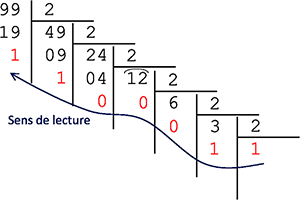
99 = (1100011)2

187 = (10111011)2

238 = (11101110)2

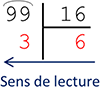
99 = (63)16

187 = (BB)16

238 = (EE)16

f. Convertir les valeurs suivantes en base 2

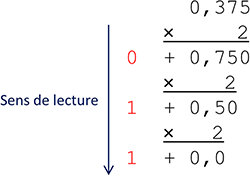
132,375

Partie entière :

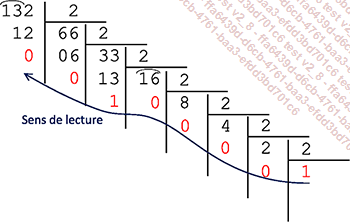
Partie décimale :

132,375 = (10000100,011)2

47,076171875 = (101111,000100111)2

1222,7705078125 = (10011000110,1100010101)2

2. Algorithme de conversion

Algo convertirB10versBx  
# Convertit un nombre écrit en base 10 en une autre base  
Variable n, base : entier  
Début  
   n <- saisir("Nombre à convertir : ")  
   base <- saisir("Base d'arrivée : ")  
   écrire("Conversion avec la méthode des divisions successives")  
   convertirB10versBxDiv(n, base)  
   écrire()  
Fin  
  
Procédure afficher(chiffre : entier)  
# Affiche un chiffre dans une base < 36  
Début  
 ...