Autour des données

Présentation du chapitre

Dans ce chapitre nous allons cheminer à travers diverses techniques et représentations de la donnée structurée (tableaux de classes et de chiffres) en complément à ce que nous avons déjà abordé.

Précédemment, en ce qui concerne l’interprétation des données, le point de vue développé était celui de la préparation des données avant leur usage dans un algorithme supervisé ou non, en grande partie pour les rendre ingérables par cet algorithme. Ici, à la demande de nos lecteurs, nous nous intéressons à la manipulation de la donnée en soi, à la fois pour la préparer, mais aussi pour être à même d’émettre de premières hypothèses ou d’avoir de premières intuitions sur sa signification. Évidemment, les deux points de vue sont complémentaires !

L’agencement de ce chapitre ne doit pas être interprété comme un "protocole" ou une méthode d’analyse de la donnée. Nous avons fait un choix didactique qui introduit pas à pas divers outils, ou qui présente la même chose sous divers angles, afin que le lecteur dispose d’éléments complémentaires à ce qu’il sait déjà, pour qu’il...

Appréhension directe et rapide d’un dataset

Afin d’éviter des redondances inutiles, nous allons nous doter d’un dataset dont les données seront utilisées dans le chapitre qui traite de la création d’un modèle sans programmation via un outil comme le logiciel BigML. Le package mlbench permet d’accéder à ces données et également de fabriquer des datasets adaptés à un type de problème.

library(tidyverse) 
library(mlbench)           # package pour créer ou accéder à des données de test 

On peut facilement lister l’ensemble des datasets de démonstration proposés dans les packages qui sont installés sur une machine.

data(package = .packages(all.available = TRUE)) # liste des datasets disponibles 

Voici un (très) court extrait de ce qui est disponible sur notre machine :

... 
Data sets in package ‘mlbench': 
 
BostonHousing                Boston Housing Data 
BreastCancer                 Wisconsin Breast Cancer Database 
DNA                          Primate splice-junction gene sequences (DNA) 
Glass                        Glass Identification Database 
HouseVotes84                 United States Congressional Voting Records 1984 
Ionosphere                   Johns Hopkins University Ionosphere database 
LetterRecognition            Letter Image Recognition Data 
Ozone                        Los Angeles ozone pollution data, 1976 
PimaIndiansDiabetes          Pima Indians Diabetes Database 
... 

Nous allons invoquer les données suivantes :

data(PimaIndiansDiabetes)  # accès aux données diabète...

Analyse de la conformation des distributions par rapport à la loi normale

On peut valider certaines de nos intuitions par rapport à la normalité des données en confrontant ces densités à la loi normale en utilisant un diagramme Quantile-Quantile. 

# ajustements loi normale(mu,e) 
plot_qq(df)          # diagrammes Quantile-Quantile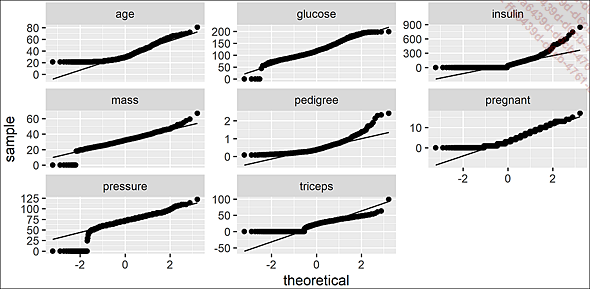 

Diagrammes Quantile-Quantile

Même sans savoir interpréter finement un tel diagramme, cela attire notre attention sur certaines caractéristiques des données :

On peut comparer cet ajustement en distinguant...

Dépendance linéaire entre variables

En complément, il est d’usage de vérifier si certaines des variables explicatives ne sont pas en forte corrélation, ce qui pourrait inciter à essayer des modèles de prédiction qui ne garderaient que l’une ou l’autre de ces variables (pour bien faire, on compare l’efficacité avec l’une et avec l’autre, et quand elle est similaire, on conserve la variable la plus facile à interpréter ou à collecter dans le monde réel).

plot_correlation(df) # un tableau de corrélations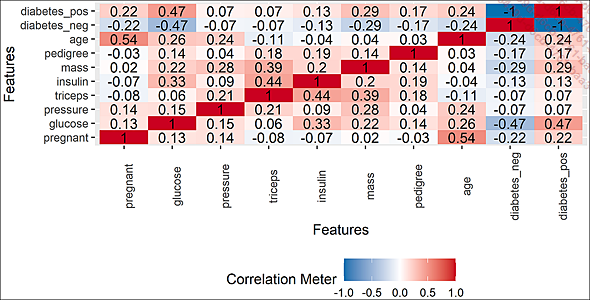 

Corrélations deux à deux

Notre problème n’est pas linéairement trivial, le diabète n’est manifestement pas corrélé simplement à une variable. Excepté pour la variable age, il semble totalement exclu qu’il y ait une part de relation plus ou moins linéaire et simple entre le nombre de grossesses et les autres variables explicatives. On peut se représenter cela, peut-être à tort, en imaginant qu’il serait intéressant de réfléchir à imaginer deux grandes familles de prédicteurs : prédicteurs "sociaux" (âge, nombre de grossesses) et prédicteurs techniques (les autres). Tout cela étant posé, remarquez que cette piste ne porte que sur des relations linéaires...

Mise en évidence de différences sur les distributions

Nous allons maintenant tâcher de mettre en évidence (ou non) d’éventuelles différences de distributions pour certaines variables d’aspect gaussien (pour cet exemple, nous avons choisi glucose) entre la distribution avec diabète ou non.

Notre préoccupation principale sera la significativité de l’éventuelle différence de moyenne. L’outil nous donne également des informations sur la différence d’écart-type, qui ne nécessite pas d’interprétation forte, sinon que le fait qu’elle soit significative peut nous conforter dans l’idée qu’un algorithme judicieux saura en extraire des améliorations de prédictibilité du diabète.

library(lessR)                                  
d <- df                         # par défaut lessR utilise d comme dataset 
tt.brief(glucose ~ diabetes)    # graphique et stats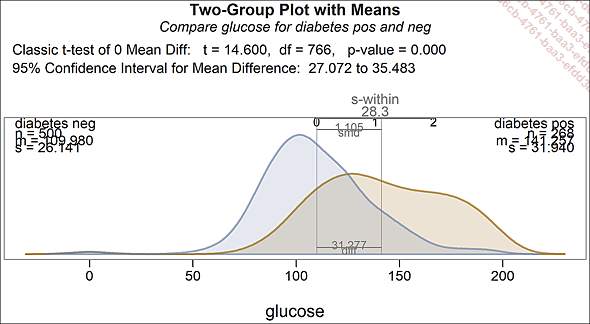 

Distributions du glucose en fonction du diabète

La différence de moyenne est significative !

Vous pourriez aussi vouloir une représentation en "moustache/violon", en utilisant la syntaxe suivante :

library(ggstatsplot) 
 
set.seed(666) ...

Points étrangers

Nous avons déjà travaillé sur l’identification d’outliers. La représentation suivante va permettre d’extraire des observations candidates à ce que vous les qualifiiez comme points étrangers. C’est à vous de choisir par essais successifs de différents paramètres le pouvoir plus ou moins discriminant du contour que vous allez tracer. Il vous reste à étudier individuellement les points à l’extérieur, dont l’identifiant est stipulé, pour commencer à envisager votre stratégie de traitement de ce type de point.

Le fait de conserver des points techniquement aberrants (anomalies ou pas) peut être valide ou non, suivant le traitement que vous appliquez sur ces valeurs. Le fait de conserver ou pas des points correspondant à des observations exceptionnelles peut vous aider à diminuer l’overfitting ou, à l’inverse, diminuer la prédictibilité de vos modèles. Toute décision de ce type doit être soigneusement consignée comme hypothèse structurante dans la documentation de vos modèles. Vous serez souvent amené à challenger ces hypothèses et à faire évoluer vos positions quant à celles-ci pour améliorer votre travail. Ne prenez pas pour argent comptant les assertions que vous pouvez...

Tris et agrégats

# une petite fonction pour imprimer head + tail d'un objet data 
h_t <- function(x, titre = "", sous_titre ="", n = 3) 
         { 
          cat(titre, "\n") 
          cat(sous_titre, "\n") 
          print(rbind(head(x,n),tail(x,n))) 
         } 

# tri à plat sur 2 var discrètes 
t <- table(df$pregnant,df$diabetes)             # tri simpliste   
h_t(t, 
   "6 lignes extraites d'un simple tri à plat, nb grossesses vs statut diabète",  
   "----------" 
   ) 
 
6 lignes extraites d'un simple tri à plat, nb grossesses vs statut diabète  
----------  
  neg pos 
0   73  38 
1  106  29 
2   84  19 
14   0   2 
15   0   1 
17   0   1 

t <- addmargins(table(df$pregnant,df$diabetes)) # tri avec les sommes 

6 lignes, tri à plat avec sommation, nb grossesses vs statut diabète  
---------------  
   neg pos Sum 
0    73  38 111 
1   106  29 135 
2    84  19 103 
15    0...