Feature Engineering

Feature Engineering, les bases

Avec moins de 100 000 entrées dans Google, le Feature Engineering, que l’on pourrait traduire avec un peu d’imagination comme étant le Génie des données, pourrait sembler le parent pauvre du machine learning et de ses 20 millions de liens. Pourtant, celui-ci représente souvent plus de la moitié de l’effort à fournir sur un projet de data sciences.

PCA classique, éléments mathématiques

Cette petite section devrait vous permettre de lire et déchiffrer avec profit la littérature sur la PCA et donne un aperçu de quelques techniques matricielles courantes (dont le changement de base).

Avec les conventions suivantes :

Réduction des données (data reduction)

Cette petite section ne concerne pas stricto sensu le "Feature Engineering", mais a également trait au nettoyage des données avant l’utilisation d’un algorithme, souvent lié au machine learning. Comme la confusion est courante, jetons un œil sur cette notion. Ici le problème est inverse, la préparation ne porte plus sur les "colonnes" mais sur les "lignes".

Cette opération consiste dans l’extraction puis l’utilisation d’un sous-ensemble cohérent de lignes issues d’un dataset de grand volume. Elle est parfois utile pour économiser des ressources machines, mais aussi pour améliorer l’efficacité de certains algorithmes ou pour en diminuer l’exposition au "bruit".

Cette notion de bruit est tout à fait intuitive dans le cas de l’interprétation d’images ou de sons, où on est habitué à l’idée que les capteurs soient moins efficaces que souhaité et y introduisent du "bruit". Ce problème d’introduction de bruit n’est pas propre aux capteurs "physiques" : du "bruit" peut être introduit accidentellement dans n’importe quel type de données en fonction du processus de captation de l’information.

Une des techniques...

Réduction de la dimensionnalité et entropie

Il peut à juste titre sembler gênant de baser toute sa stratégie de réduction de la dimensionnalité sur l’algèbre linéaire, comme on le fait avec la PCA, car ces techniques pourraient embarquer certaines hypothèses simplificatrices sur la nature des données sur lesquelles le data scientist a peu de prise.

Le concept "d’entropie et d’information partagée" décrit dans l’introduction de cet ouvrage semble plus général et il semble donc légitime de bâtir une part de sa stratégie sur ces concepts.

Dans le chapitre Introduction, nous avons exprimé l’information mutuelle de deux variables comme étant représentable par l’expression suivante (en fonction de l’entropie) : I(X,Y) = H(X) + H(Y) - H(X,Y)

Cette expression s’annulant dans le cas de deux variables dépendantes. Ici la notion de dépendance ne suppose pas une dépendance linéaire ou même une dépendance linéaire après une quelconque transformation.

1. Description théorique du problème

Nous allons appeler S (comme set) l’ensemble de nos variables explicatives x_i et y notre variable de réponse.

Notre objectif est de sélectionner un sous-ensemble de S comportant p features, à savoir certaines variables explicatives (features), nous nommerons ce sous-ensemble s et m son nombre de features.

Il nous faut donc un critère de sélection.

En première approximation, on imagine rapidement qu’il faut trouver l’ensemble de features s qui possède la plus grande dépendance avec la cible y. En effet, si un ensemble de features possède plus d’informations mutuelles qu’un autre avec la cible, cet ensemble sera le plus à même de prédire la cible.

Comme nous avons décidé d’utiliser l’information mutuelle, notre mesure de dépendance sera .

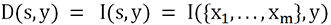L’idée sera alors d’explorer toutes les possibilités d’ensemble s inclus dans S, de calculer cette dépendance et de retenir la plus élevée.

Ce qui, dès que p est peu grand, induit à calculer un très grand nombre de combinaisons d’informations...