Compléments utiles
GAM : généralisation de LM/GLM
Pour aller plus loin avec le modèle linéaire nous allons étudier sa généralisation, qui fait, à juste raison, partie de la boîte à outils de nombreux data scientists.
Le modèle additif généralisé (GAM) va plus loin que le modèle GLM dans la généralisation des modèles linéaires, aussi faut-il se doter de celui-ci dès le début de vos travaux.
C’est un modèle très maniable, aux grandes possibilités, efficace en termes de performance, dont les qualités peuvent inciter à des comportements d’overfitting car il permet de faire ce que nous pourrions appeler du "cousu main" sur les données. Mais c’est aussi un modèle qui incite à comprendre et analyser ses données et qu’il est très intéressant d’utiliser dans une optique courageuse et exploratoire.
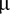 et de variance
et de variance 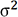 avec
avec 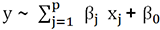 .
.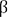 , qui sont
toujours les paramètres à découvrir !
, qui sont
toujours les paramètres à découvrir !Dans ce modèle, la variable de réponse peut ne pas correspondre à une distribution...
Manipulation d’images
La manipulation d’images permet d’extraire différentes features de celles-ci ou de les prétraiter avant l’application de divers algorithmes (typiquement un traitement au travers d’un réseau neuronal).
Nous allons aborder ces manipulations de façon syntaxique et sans fioriture, l’idée étant de vous inciter à aller plus loin en découvrant la simplicité des outils déjà à votre disposition.
Manipuler des images, c’est aussi évoluer dans un monde spatial en deux et trois dimensions, comme en géographie, où deux dimensions sont les variables explicatives de la troisième (intensité, couleur). Une autre similarité avec les usages géographiques et géophysiques s’avère être que les dimensions spatiales sont à considérer de façon conjointe au travers de leur covariance, par exemple : la distance entre deux yeux est plus représentative des caractéristiques d’un visage que l’écart des valeurs de leurs coordonnées respectives.
Dans une image se cachent, tout comme en géographie, d’autres variables latentes et parfois dimensionnelles (ex : la profondeur). Au même titre que l’eau est plus souvent au fond des ravins, les ombres d’un visage apparaissent plus souvent dans les creux du visage que sur la pointe de son nez.
Notre travail sur les dimensions 2D et 3D commence donc par un travail sur l’image, puis nous enchaînerons sur d’autres aspects de la spatialité. Retenez également qu’il existe un continuum de pensée entre les dimensions 1D/2D des séries temporelles et les dimensions 2D/3D de l’image, de la géographie, de la propagation des sons ou des ondes. Si bien que les techniques de modélisation, d’optimisation ou de prédiction acquises dans un de ces champs d’investigation sont utiles dans les autres (moyennant quelques changements de vocabulaire et de contrainte).
1. Création, visualisation, lecture et écriture d’images
Une image en noir et blanc peut se stocker sous la forme d’une matrice de pixels (hauteur et largeur de l’image). Chaque pixel ayant une intensité plus ou moins forte (son intensité...
Comment créer un échantillon : LHS (hypercube latin)
Pour créer un échantillonnage efficace, en particulier quand le problème possède de nombreuses dimensions, il est tentant de fabriquer un échantillonnage où on retrouve un minimum d’interactions entre les variables. Évidemment, ce type d’échantillonnage est d’autant plus utile que l’on soupçonne une faible covariance entre celles-ci, car ce mode d’échantillonnage ne va pas facilement aider à capturer l’effet des interactions entre variables.
Dans le cas des problèmes en petite dimension (2D, 3D) mais avec beaucoup de points par paquet d’observations (image, géographie...), ces méthodes d’échantillonnage trouvent également tout leur sens.
Les joueurs d’échecs connaissent le problème des huit reines sur un échiquier, qui consiste à poser sur l’échiquier huit reines qui ne seront pas en prise. Les carrés magiques, les sudokus et les huit reines sont des problèmes de construction d’une répartition d’objets sous des contraintes d’interaction précises et souvent minimales.
LHS (Latin Hypercube Sampling) ressemble à un problème de "tours" d’un jeu d’échecs, chaque tour ne devant pas être en prise avec...
Travailler sur des données spatiales
1. Variogramme
a. Champ et variable régionalisée
Pendant la séquence "météo" à la télévision, le présentateur commente une carte sur laquelle sont reportées les températures : il vous désigne un champ scalaire (scalar field).
À chaque emplacement, défini par ses coordonnées en 2D sur la carte, il existe une température (une valeur scalaire). Sur la carte météo, seuls certains points sont affublés d’une température, c’est un échantillonnage : on aurait pu choisir ces points en utilisant LHS, mais on a sans doute préféré stipuler les températures aux points correspondant aux différentes grandes villes.
Pour en déduire la température chez vous, dans le cas où vous n’habitez pas dans une grande ville, il vous faut interpoler (en effectuant un lissage). Vous disposez d’une infinité de stratégies plus ou moins efficaces : un lissage brutal en utilisant les deux villes les plus proches et en faisant une moyenne, le même lissage en faisant une moyenne pondérée par l’inverse des distances, l’utilisation de trois villes qui forment un triangle autour de vous et le calcul des coefficients de pondération comme étant l’inverse des coefficients barycentriques de votre emplacement vu comme barycentre des trois villes...
Quand le présentateur météo vous commente efficacement la situation des vents sur la carte, il vous donne la vitesse du vent, mais aussi sa direction : il a donc défini des vecteurs "vents" à divers endroits de la carte. Parfois de petites flèches plus ou moins longues représentent ces vitesses en tout point de la carte. Nous sommes en train de parler d’un champ vectoriel (vector field).
Un pilote de montgolfière ne se contenterait sûrement pas de champs en 2D sur la carte, il voudra sans doute connaître la force des vents et leur direction en trois dimensions, par exemple : le vent à 100 m d’altitude à telles coordonnées GPS est ascendant et N-Nord-Ouest, 60 km/h.
La différence entre les valeurs d’un champ scalaire entre deux points peut générer un...
Savoir-faire utiles
1. Tracer une courbe ROC
Nous avons introduit la courbe ROC et la notion d’AUC dans le premier chapitre. Le concept n’est pas très compliqué, mais on a parfois des difficultés à tracer ces courbes de prime abord. Ce sont des courbes attendues par vos pairs, voici donc un code "hyper classique" pour en produire une.
Pour fabriquer notre jeu de données, nous avons repris le code LHS vu plus haut, mais avec 300 observations au lieu de 100.
Notre exemple utilise les arbres de décision. Nous avons fabriqué une fonction perturbée pour produire des classes binaires. Cette partie de code est sans surprise.
require(caret)
require(party)
set.seed(1)
y <- 10*df[,1] + # une fonction étrange
7* df[,2] * rnorm(nrow(df))+
3*sin(df[,3])+
2*sin(df[,4])*runif(nrow(df))
y <- ifelse(y < 7,0,1) # fabrication de classes
sum(y)/length(y) # % classes
y <- factor(y) # création facteurs
df_<- data.frame(df,y) # plus simple pour :
p <- createDataPartition(y=df_$y,
p= 50/100,
list=FALSE)
training <- df_[p,]
test <- df_[-p,]
#---------------------------------------------------------------#
# ctree #
m <- ctree(y~.,data=df_) # arbres
m
y.pred <- predict(m,test) ...Gradient Boosting et Generalized Boosted Regression
1. Les grands principes
Les principes du boosting et des méthodes de gradient ont déjà été présentés dans les chapitres précédents (dès le premier chapitre). Nous allons maintenant nous focaliser sur une implémentation pratique, particulièrement facile à manipuler pour des datasets de taille raisonnable comme ceux que vous croiserez dans les concours de data scientist : la Generalized Boosted Regression.
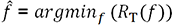 .
.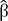 estimés de la fonction tels que
estimés de la fonction tels que 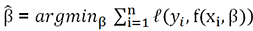 .
.Dans le cas non paramétrique, on reste sur la première formulation en fonction du risque et la méthode du gradient s’applique directement sur le risque.
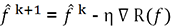 .
.Mais dans le cas paramétrique, il est possible d’appliquer la méthode du gradient directement sur les paramètres, ce que l’on ne se prive pas de faire.
Tout cela pose quelques problèmes pratiques. En effet le modèle a tendance à s’overfitter sur l’ensemble des observations (plutôt que de créer une fonction résultante généralisable). Les cas où des observations différentes avec les mêmes valeurs explicatives débouchent sur une réponse différente peuvent déstabiliser la descente de gradient (ce n’est pas pour rien que l’on a mis au point d’autres méthodes d’optimisation telles que celles que nous avons vues plus haut !).
Une conclusion pratique (cf. l’œuvre de Friedman) est de baser la descente...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations