Analyse en composantes principales
Objectif du chapitre
Les algorithmes du Machine Learning permettent principalement de réaliser des regroupements, des classifications et des régressions dans l’objectif d’analyser les données et/ou de construire des modèles prédictifs sur ces données. Le plus souvent, ces données sont définies dans des espaces de très grande dimension. Cela cause deux problèmes majeurs, à savoir :
-
Plus la dimension est élevée, plus les données sont éparses, ce qui rend la tâche des algorithmes de prédiction plus compliquée et très sensible à la généralisation.
-
La représentation graphique de ces données devient quasiment impossible puisque les capacités de visualisation de l’œil humain sont limitées à un nombre de dimensions d≤3.
À partir de ce constat, le besoin de réduire la dimension des données devient important. L’objectif de ce chapitre est d’introduire l’ACP (Analyse en Composantes Principales) qui est l’une des méthodes les plus utilisées pour la réduction de dimensions.
À la fin de ce chapitre, le lecteur aura appris :
-
ce qu’est l’ACP et à quoi elle sert,
-
les aspects analytiques associés à l’ACP,
-
comment mettre en œuvre une ACP et interpréter...
Pourquoi l’ACP ?
Les données de grande dimension posent des problèmes liés à la pertinence des modèles prédictifs. Mais avant tout, cette grande dimension pose des problèmes de visualisation. En effet, l’œil humain est un outil très puissant qui, à partir d’un simple graphique et en quelques fractions de seconde, peut détecter des regroupements d’individus et des liaisons entre les variables. Ces informations sur les individus et les variables peuvent naturellement être exploitées et utilisées pour la construction de modèles prédictifs performants. Le problème est que si les données sont exprimées dans un espace de dimension supérieur à trois, l’œil humain devient inutile. Dans la pratique, le plus souvent, les données appartiennent à des espaces nettement supérieurs à cette limite humaine. Pour en être convaincu, il suffirait par exemple de faire un tour sur le site www.kaggle.com où plusieurs compétitions sont proposées aux Data Scientists et aux amateurs de l’intelligence artificielle. Ces compétitions portent sur des problèmes réels issus du monde des entreprises et des laboratoires de recherche.
Il existe plusieurs méthodes qui permettent de synthétiser les informations d’un nuage de points...
L’ACP du point de vue géométrique
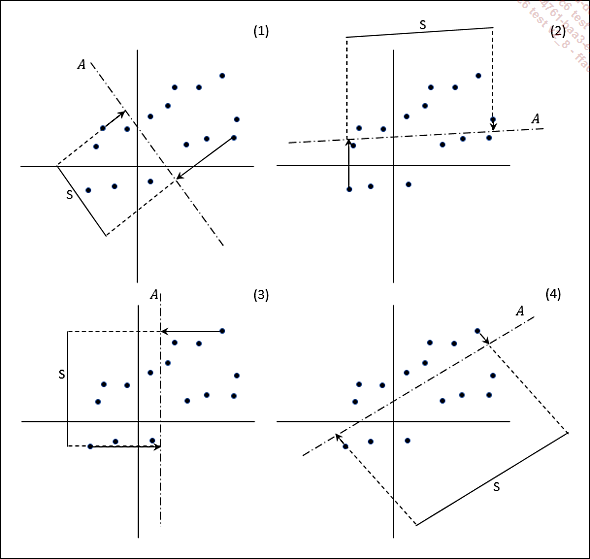
Figure 12-1 : projection d’un nuage de points sur différents axes
Afin de donner une vision géométrique et intuitive de l’ACP, considérons le nuage de 15 points défini dans un espace à deux dimensions et représenté dans les quatre graphiques de la figure 12-1. Pour passer de cet espace à deux dimensions à un espace plus petit à une dimension, il faudrait procéder à la projection sur un seul axe de tous les points du nuage. Comme il existe une infinité d’axes de projection possibles, la question qui se pose immédiatement est la suivante : comment choisir cet axe pour qu’à la fin de la projection l’information totale présente dans le nuage de points initial soit déformée le moins possible sur ce nouvel axe ?
Dans chacun des graphiques ci-dessous, le nuage de points est projeté sur un axe A différent. Vous remarquerez que la différence entre les quatre projections se situe essentiellement au niveau de la taille du segment S contenant toute la projection du nuage sur l’axe A.
La projection d’un nuage de points défini dans un espace à plusieurs dimensions dans un autre espace de dimension inférieure ne peut que déformer l’information présente dans ce nuage projeté. Cependant...
L’ACP du point de vue analytique
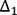 le plus
proche du nuage de points étudié (voir la figure
12-2 ci-dessus). En d’autres termes, nous recherchons un axe
le plus
proche du nuage de points étudié (voir la figure
12-2 ci-dessus). En d’autres termes, nous recherchons un axe 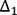 tel que la quantité :
tel que la quantité : 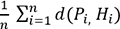 est maximale avec
est maximale avec 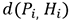
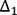 et n le
nombre de points dans le nuage.
et n le
nombre de points dans le nuage.En appliquant le théorème de Pythagore, cela revient à maximiser la quantité :
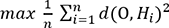 (1)
(1)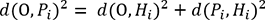
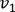 qui a la
même direction que l’axe
qui a la
même direction que l’axe 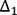 et qui maximise la formule suivante :
et qui maximise la formule suivante :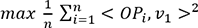 (2)
(2)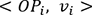 le produit
scalaire entre le vecteur associé au point Pi et le vecteur
le produit
scalaire entre le vecteur associé au point Pi et le vecteur 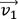 . Pour simplifier la formulation, nous allons
noter OPi par simplement Pi.
. Pour simplifier la formulation, nous allons
noter OPi par simplement Pi.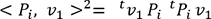 (3)
(3)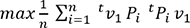 (4)
(4)Le produit scalaire est symétrique, donc la formule (4) devient :
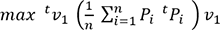 (5)
(5)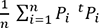 n’est rien d’autre que la matrice de variance/covariance S du nuage de points initial, ou
la matrice des corrélations si le nuage de points est centré et
réduit. Donc la formule (5) devient :
n’est rien d’autre que la matrice de variance/covariance S du nuage de points initial, ou
la matrice des corrélations si le nuage de points est centré et
réduit. Donc la formule (5) devient :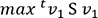 (6).
(6).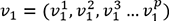 les inconnues du problème. Ce problème
admet une infinité de solutions puisque, pour tout...
les inconnues du problème. Ce problème
admet une infinité de solutions puisque, pour tout...Indicateurs de la qualité de la représentation des données
Les sections précédentes ont montré qu’une ACP est une projection d’un nuage de points qui permet d’avoir une vue simple, représentable en deux ou trois dimensions, et synthétique puisqu’elle résume les données étudiées. Cependant, l’ACP n’est pas une fin en soi, il faudrait donner un sens métier à ces résultats. Par exemple, à partir des résultats, nous pouvons constater des regroupements d’individus, ou encore de fortes liaisons, corrélations entre certaines variables. Il existe des indicateurs qui peuvent nous aider à l’interprétation des résultats d’une ACP. Comme nous allons le voir par la suite, ces indicateurs sont liés soit aux individus, soit aux variables.
1. Indicateurs liés aux individus
Une fois que le nuage de points est projeté dans un nouvel espace formé par les composantes principales, nous disposons de plusieurs métriques permettant de nous indiquer la qualité de la représentation des individus par cette projection.
Ainsi, les trois sections suivantes montrent comment calculer :
-
le score d’un individu ;
-
la contribution d’un individu à l’information apportée par une composante principale ;
-
la qualité de la représentation d’un individu par une composante principale.
a. Score des individus
Exemple d’ACP avec Python
Afin de mieux comprendre les aspects théoriques abordés dans ce chapitre, nous allons réaliser une ACP sur un exemple illustratif. Nous avons volontairement choisi un jeu de données pour lequel nous avons une bonne idée des résultats que nous devrions obtenir avec l’ACP.
Ce jeu de données est défini dans le fichier notes_étudiants.csv du dossier Data de ce chapitre et il est composé de 33 observations. Chaque observation correspond aux résultats d’un étudiant dans 10 matières différentes. Les individus qui composent notre nuage de points sont donc des étudiants, et les variables sont les matières suivantes : Mathématiques, Physique, Sciences naturelles, Histoire, Géographie, Philosophie, Français, Anglais, Allemand et Sport. Également, chaque étudiant est identifié de façon unique avec la variable id.
En réalité, nous avons construit manuellement les données de cet exemple afin de dissimuler intentionnellement un certain nombre d’informations et de voir si l’ACP permettrait de retrouver toutes ces informations à l’aide de graphiques tracés sur des plans à deux dimensions.
Ainsi, les données de cet exemple ont été construites de la manière suivante :
-
Domaines des variables :
-
Toutes les variables sont définies dans l’intervalle [2,20] sauf la variable Sport qui est définie dans l’intervalle [5,10].
-
-
Les profils des étudiants : nous avons créé sept profils représentés avec les groupes G1, G2, G3, G4, G5, G6 et G7 définis ci-après.
-
Le profil formé par le groupe G1:{id=4, id=6, id=12, id=28, id=32}, composé de cinq étudiants qui ont de bonnes notes dans les six matières Mathématiques, Physique, Sciences naturelles, Histoire, Géographie et Philosophie. Ces notes sont comprises dans l’intervalle [16,20]. Aussi, les étudiants de ce groupe ont des notes proches de la moyenne qui varie dans l’intervalle [8,13] dans les matières Français, Anglais, Allemand.
-
Le profil formé par le groupe G2:{id=1, id=2, id=22, id=24, id=27}, composé de cinq étudiants...
-
Conclusion
Dans ce chapitre, nous avons abordé l’Analyse en Composantes Principales. Nous avons commencé par expliquer les objectifs de l’ACP et les problèmes qu’elle tente de résoudre. Nous avons essayé de donner l’intuition derrière l’ACP, puis nous avons donné la preuve formelle que les vecteurs propres de la matrice de données sous-jacente au nuage de points analysé correspondent aux axes principaux de l’ACP. Nous avons proposé de réaliser une ACP sur un exemple illustratif afin d’assimiler les concepts théoriques et de montrer comment Scikit-learn facilite l’application d’une ACP.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations