Editions ENI Livres | Vidéos | e-Formations
La régression logistique
Objectif du chapitre
Le modèle de la régression logistique est un cas particulier de modèle linéaire généralisé et c’est l’un des modèles de classification les plus répandus. Il est utilisé dans des domaines tels que le domaine médical, le domaine social ou le domaine bancaire : par exemple, détecter la présence ou non d’une tumeur chez un patient, expliquer un risque suicidaire après une dépression nerveuse, ou encore prédire si un client pourra ou non rembourser son crédit. De façon plus générale, avec la régression logistique, on cherche à détecter les prémisses de la survenue d’un phénomène.
L’objectif de ce chapitre est d’expliquer les notions de base de la régression logistique et de montrer un exemple de modèle de régression logistique développé avec Scikit-learn.
À la fin de ce chapitre, le lecteur aura abordé :
-
une justification et l’intuition des algorithmes de régression logistique,
-
quelques notions théoriques de la régression logistique,
-
l’application de la régression logistique pour prédire les survivants du naufrage du Titanic en utilisant la bibliothèque Scikit-learn,
-
le seuil de décision d’un modèle...
La régression logistique
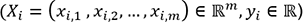, avec yi le résultat
obtenu pour l’observation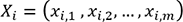 
, alors on
peut construire un modèle prédictif linéaire de
la forme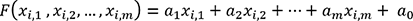 
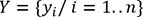est une variable binaire ou une variable qualitative,
alors il n’est plus question de prédire un nombre réel,
mais plutôt la classe associée à une
observation. Dans ce dernier cas, le but recherché est
un modèle de classification, et les modèles de
régression linéaire ne sont plus adaptés
puisque la fonction linéaire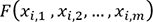 
est définie dans 
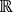.Comme nous allons le voir dans la suite de ce chapitre, l’idée de la régression logistique est de transformer le problème de l’explication d’une variable continue en un problème d’explication d’une probabilité. En d’autres termes, les algorithmes de régression logistique sont une adaptation des algorithmes de régression afin de ne plus prédire une valeur réelle, mais plutôt une classe d’appartenance associée à une observation.
Supposons que nous disposons...
Prédire les survivants du Titanic
1. Définition du jeu de données Titanic
Dans cet exemple, un jeu de données très connu dans la communauté des Data Scientists sera utilisé. Il s’agit d’un sous-ensemble des passagers du fameux navire Titanic. L’objectif de cet exemple est de construire un modèle qui sait prédire pour un passager particulier s’il a survécu ou pas à ce drame. Ce jeu de données indique pour chaque passager les informations suivantes :
-
PassengerId : identifiant d’un passager.
-
Survived : variable binaire indiquant si le passager a survécu au drame ou non.
-
Pclass : variable indiquant la classe de la cabine. Elle prend ses valeurs parmi les valeurs 1, 2 et 3 qui correspondent respectivement à la première, seconde et troisième classe.
-
Sex : variable indiquant le sexe du passager, Male ou Female.
-
Age : variable indiquant l’âge du passager.
-
SibSp : variable indiquant si le passager a des frères, des sœurs, un époux ou une épouse à bord du bateau.
-
Parch : variable indiquant si le passager a des parents ou des enfants à bord du bateau.
-
Fare : prix du ticket.
-
Embarked : port d’embarcation (C = Cherbourg, Q = Queenstown, S = Southampton).
En résumé, l’objectif est de prédire la variable Survived à partir des valeurs des variables Pclass, Sex, Age, SibSp, Parch, Fare et Embarked. La variable PassengerId ne sera pas utilisée, car nous supposons qu’elle n’a pas d’impact sur la variable Survived.
2. Réalisation du modèle de régression logistique
Afin de construire un modèle de régression logistique avec Scikit-learn pour prédire la variable Survived, suivez les étapes ci-après.
Commencez par la création d’un nouveau notebook Jupyter, vous pouvez utiliser le notebook 08-régression_logistique.ipynb contenu dans le sous-dossier Code de ce chapitre.
a. Chargement des modules Scikit-learn
Dans la première cellule de votre notebook, saisissez les instructions suivantes, puis exécutez cette cellule afin d’importer les modules nécessaires à la réalisation de notre modèle :
import matplotlib.pyplot as plt ...L’algorithme One-vs-All
Ce chapitre s’est focalisé sur la régression logistique binomiale, qui traite des modèles dont la variable à prédire est binaire. Cependant, la régression logistique peut être généralisée à des variables prédictives multiclasses, qui peuvent donc prendre un nombre de modalités supérieur à deux. Dans ce dernier cas, l’algorithme One-vs-All est sans doute l’algorithme le plus utilisé.
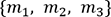. Pour calculer la probabilité que 
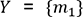, cet algorithme va construire deux groupes :
le premier groupe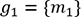 
et le deuxième
groupe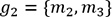 
. Maintenant, le problème
est transformé en un problème binaire où il
faudrait prédire si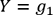 
ou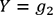 
. On suit
le même raisonnement pour calculer la probabilité que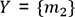 
avec 
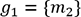et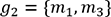 
. Enfin, pour calculer la probabilité que 
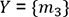, on fixe 
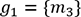et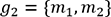 
. Une fois
que ces trois probabilités sont calculées, il
suffit de choisir la probabilité la plus élevée
afin de prédire la classe d’une observation.Conclusion
La régression logistique est un modèle très répandu dans le monde du Machine Learning. Il trouve son application dans des domaines divers et variés. Ce chapitre a permis de donner l’intuition de ce modèle ainsi que d’aborder quelques concepts justifiant plus au moins sa complexité vis-à-vis des modèles linéaires. Il nous a également permis de voir comment construire un modèle de régression logistique avec Scikit-learn pour prédire les survivants du naufrage du Titanic. Enfin, nous avons expliqué l’algorithme One-vs-All qui permet de traiter les problèmes de classification multiclasse.
