Statistiques
Objectif du chapitre
Les statistiques regroupent un ensemble de méthodes dédiées à l’échantillonnage de données ainsi qu’à leur analyse afin de tirer des conclusions et de comprendre les phénomènes sous-jacents à ces données. Ces méthodes statistiques font partie intégrante de la Data Science.
Il est quasiment impossible d’aborder l’ensemble des méthodes statistiques en un seul ouvrage vu leur diversité. Il existe plusieurs livres qui traitent des statistiques. L’objectif de ce chapitre est double : le premier est la présentation des outils statistiques élémentaires que tout Data Scientist devrait connaître, et le deuxième objectif est d’attirer l’attention du lecteur sur l’intérêt des statistiques et leur relation avec la Data Science. Ainsi, nous allons porter une attention particulière à la partie inférentielle des statistiques.
À la fin de ce chapitre, le lecteur aura abordé :
-
les statistiques descriptives,
-
les lois de probabilité,
-
la loi normale et la loi normale centrée réduite,
-
le principe de l’échantillonnage,
-
le théorème central limite,
-
l’estimation ponctuelle,
-
l’estimation par intervalle de confiance,
-
les tests d’hypothèses,
-
le paradoxe de Simpson....
Les statistiques descriptives
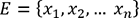 , nous pouvons calculer certains
paramètres afin de cerner la nature de la distribution
associée aux valeurs
, nous pouvons calculer certains
paramètres afin de cerner la nature de la distribution
associée aux valeurs 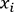 .
.Ainsi, nous distinguons deux types de paramètres que nous pouvons calculer sur une série statistique de type quantitative : les paramètres de position et les paramètres de dispersion présentés dans les sous-sections suivantes.
1. Paramètres de position
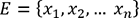 .
.a. La moyenne
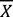 associée à une série
de valeurs
associée à une série
de valeurs 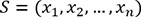 se calcule comme
suit
se calcule comme
suit 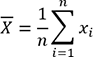 .
.La moyenne ainsi calculée correspond à la moyenne arithmétique. Il existe d’autres types de moyennes telles que la moyenne harmonique, la moyenne quadratique ou encore la moyenne géométrique. Généralement, en statistiques, la moyenne utilisée est la moyenne arithmétique.
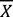 calculée sur cet échantillon
avec la moyenne de la population ! Dans la suite de ce
chapitre, nous allons revenir sur la relation entre la moyenne d’un échantillon
et la moyenne de la population.
calculée sur cet échantillon
avec la moyenne de la population ! Dans la suite de ce
chapitre, nous allons revenir sur la relation entre la moyenne d’un échantillon
et la moyenne de la population.b. Le mode
Le mode d’une série de valeurs est tout simplement la valeur qui apparaît le plus fréquemment.
Par exemple, dans la série de valeurs S=(1, 2, 5, 2, 5, 5, 6, 8, 5, 9, 5), on dira que le mode est la valeur 5, car c’est bien cette valeur qui apparaît avec le plus d’occurrences. La valeur 5 apparaît cinq fois, la valeur 2 deux fois, puis les autres valeurs apparaissent une fois chacune.
La série S de notre exemple est dite unimodale, car elle dispose d’un seul mode. La série S1=(1, 2, 5, 2, 5, 5, 2, 2, 5, 2, 5) est dite bimodale, car elle dispose de deux modes, à savoir le mode...
Les lois de probabilité
Une loi de probabilité permet de cerner le comportement d’une variable aléatoire. Dans le domaine des probabilités, une variable aléatoire dépend du hasard. Justement, c’est le comportement de ce hasard que l’on tente de décrire avec une loi de probabilité. Avec une loi de probabilité, nous pouvons calculer la probabilité qu’une variable aléatoire soit fixée à une valeur donnée.
Par exemple, si nous considérons une variable X associée au résultat obtenu après le lancer d’un dé à six chiffres, alors cette variable X sera appelée une variable aléatoire, puisque la survenue de l’un des six chiffres est un événement aléatoire.
 , alors la loi de la variable X est tout simplement
, alors la loi de la variable X est tout simplement 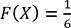 .
.Le choix d’une loi de probabilité est en fonction de la nature de la variable aléatoire étudiée et en fonction du phénomène associé à cette variable aléatoire. En effet, une variable aléatoire X peut être discrète ou continue et elle peut être définie dans un intervalle fini, semi-fini ou infini. Le phénomène...
La loi normale
La loi normale permet de modéliser une distribution suivant une courbe de Gauss. Cette loi normale joue un rôle quasiment central en modélisation statistique du fait de ses relations avec plusieurs autres lois de probabilité, et aussi du fait du théorème central limite que nous allons aborder plus loin dans ce chapitre.
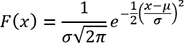 .
.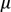 et
et 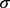 respectivement la moyenne et l’écart-type
de la variable aléatoire modélisée par
cette formule.
respectivement la moyenne et l’écart-type
de la variable aléatoire modélisée par
cette formule.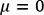 et l’écart-type
et l’écart-type 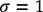 , alors la formule précédente devient :
, alors la formule précédente devient : 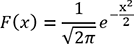 .
.Et dans ce cas, nous parlons de loi normale centrée réduite. Cette loi normale centrée réduite est également appelée la loi normale standard.
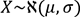 .
.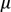 donné et un
donné et un 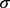 donné, nous pouvons tracer la courbe
associée à la loi normale. Comme il y a une infinité de
possibilités pour
donné, nous pouvons tracer la courbe
associée à la loi normale. Comme il y a une infinité de
possibilités pour 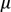 et
et 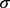 , l’utilisation de la loi normale centrée
réduite, avec
, l’utilisation de la loi normale centrée
réduite, avec 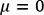 et
et 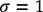 , devient intéressante, car les aires
sous la courbe de la loi normale sont les mêmes...
, devient intéressante, car les aires
sous la courbe de la loi normale sont les mêmes...L’échantillonnage
La procédure d’échantillonnage consiste à sélectionner des sous-ensembles d’individus à partir d’une population. Chacun de ces sous-ensembles d’individus constitue un échantillon. L’objectif est d’analyser ces échantillons afin d’aboutir à des conclusions généralisables sur l’ensemble de la population. La suite de cette section donne des résultats fondamentaux en statistiques sur les distributions des moyennes et des proportions associées aux échantillons.
1. Principe de l’échantillonnage
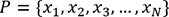 avec
avec 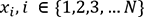 les individus
de cette population et N le
nombre d’individus de l’ensemble de la population. Sur
cette population P, des échantillons
peuvent être sélectionnés comme suit :
les individus
de cette population et N le
nombre d’individus de l’ensemble de la population. Sur
cette population P, des échantillons
peuvent être sélectionnés comme suit :
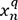 le nième individu de
l’échantillon Eq et
le nième individu de
l’échantillon Eq et 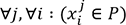 .
.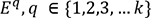 permettent d’avoir
une idée sur la répartition des données
dans la population P.
permettent d’avoir
une idée sur la répartition des données
dans la population P.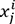 , avant de
procéder au tirage du prochain individu, il faut d’abord
remettre dans la population cet individu
, avant de
procéder au tirage du prochain individu, il faut d’abord
remettre dans la population cet individu 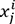 de telle sorte qu’il puisse de nouveau être tiré avec
la même probabilité que tous les autres individus.
de telle sorte qu’il puisse de nouveau être tiré avec
la même probabilité que tous les autres individus.2. Résultats sur la distribution des moyennes
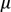 la moyenne
de la population P et
la moyenne
de la population P et 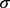 son écart-type. Si P est une population infinie ou
assimilée à une population infinie en utilisant
les tirages avec remise...
son écart-type. Si P est une population infinie ou
assimilée à une population infinie en utilisant
les tirages avec remise...Les statistiques inférentielles
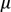 , l’écart-type
, l’écart-type 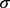 et la proportion p d’individus
possédant une caractéristique donnée
et la proportion p d’individus
possédant une caractéristique donnée 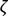 sont connus. Grâce au théorème
central limite et à partir de ces trois paramètres
connus, nous avons conclu des résultats sur les deux distributions
des deux variables aléatoires associées
respectivement aux moyennes des échantillons prélevés à partir
de la population P et aux
fréquences d’individus possédant la caractéristique
sont connus. Grâce au théorème
central limite et à partir de ces trois paramètres
connus, nous avons conclu des résultats sur les deux distributions
des deux variables aléatoires associées
respectivement aux moyennes des échantillons prélevés à partir
de la population P et aux
fréquences d’individus possédant la caractéristique 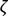 dans ces mêmes échantillons.
Avec l’estimation, nous allons considérer une population P={x1,x2,x3,…,xN} pour
laquelle les paramètres
dans ces mêmes échantillons.
Avec l’estimation, nous allons considérer une population P={x1,x2,x3,…,xN} pour
laquelle les paramètres 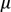 ,
, 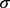 et p ne sont pas connus, et justement,
grâce aux notions que nous allons aborder dans cette section,
nous allons pouvoir estimer leurs valeurs à partir d’un
seul échantillon. C’est en ce sens que l’estimation est
le processus inverse de l’échantillonnage.
et p ne sont pas connus, et justement,
grâce aux notions que nous allons aborder dans cette section,
nous allons pouvoir estimer leurs valeurs à partir d’un
seul échantillon. C’est en ce sens que l’estimation est
le processus inverse de l’échantillonnage.En d’autres termes, dans l’échantillonnage nous sommes partis d’une population pour avoir des conclusions sur les échantillons, et avec l’estimation, nous partons d’un échantillon afin d’aboutir à des conclusions sur la population.
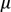 ,
, 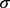 et p de
façon ponctuelle, et la deuxième méthode
consiste en l’estimation de ces paramètres avec des intervalles
de confiance. La suite de cette section donne les détails
de calcul de ces deux méthodes d’estimation....
et p de
façon ponctuelle, et la deuxième méthode
consiste en l’estimation de ces paramètres avec des intervalles
de confiance. La suite de cette section donne les détails
de calcul de ces deux méthodes d’estimation....Conclusion
Ce chapitre nous a permis d’aborder les notions fondamentales des statistiques. Nous avons passé en revue les statistiques descriptives et nous nous sommes un peu plus attardés sur les statistiques inférentielles vu leurs relations immédiates avec la Data Science. À partir de maintenant, nous allons consacrer le reste de cet ouvrage à l’étude des algorithmes du Machine Learning et nous allons mettre en pratique chacun des algorithmes abordés avec la librairie Scikit-learn.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations