Support Vector Machine

Objectif du chapitre

L’algorithme SVM fut introduit par Vapnik en 1995 et il est basé sur la théorie de Vapnik-Chervonenkis. Théoriquement, les SVM sont une généralisation des modèles de classification linéaires. Les SVM ont été appliqués avec beaucoup de succès dans divers domaines et spécialement dans le domaine de la reconnaissance de formes à partir d’images et le domaine de la bio-informatique.

Dans la littérature francophone, l’algorithme SVM est le plus souvent nommé « algorithme séparateur à vaste marge ». En effet, les algorithmes SVM se distinguent de la plupart des autres algorithmes par la maximisation de la marge qui sépare deux classes de données. Ce chapitre tente d’expliquer les SVM d’un point de vue intuitif, mais aussi analytique, tout en mettant l’accent sur cet aspect de maximisation de la marge séparatrice.

À la fin de ce chapitre, le lecteur aura abordé :

Le SVM du point de vue géométrique

Les SVM sont des algorithmes supervisés qui, au début, ont été développés pour résoudre des problèmes de classification binaire. Ils ont été généralisés pour prédire des variables quantitatives.

Dans le cas de la classification binaire, les SVM recherchent un hyperplan discriminant de marge optimale entre deux classes. Pour comprendre l’idée véhiculée par cet algorithme, cette section donne une explication intuitive basée sur des illustrations.

Dans la figure ci-dessous, deux ensembles sont représentés sur quatre graphiques à deux dimensions : le premier est composé de neuf carrés vides et le deuxième ensemble est composé de neuf cercles vides.

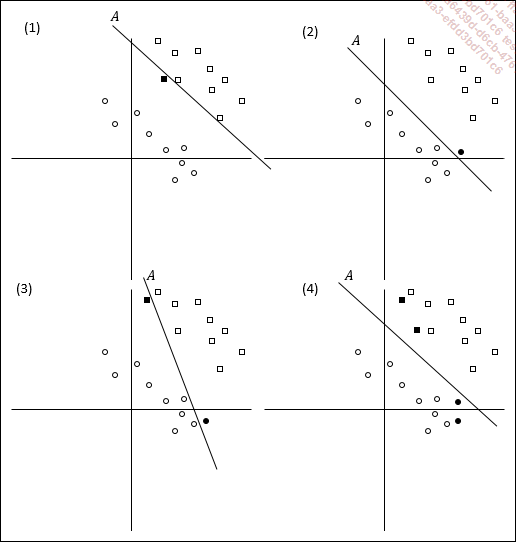
Figure11-1 : exemples de modèles linéaires

Supposons que ces carrés et ces cercles vides forment la base de données d’apprentissage et que les carrés et les cercles noirs (pleins) sont les données futures, des données encore inconnues au moment de la phase d’apprentissage.

Sans prendre en compte ces données futures, le modèle représenté par la droite (A) dans chacun des quatre repères sépare toutes les données d’apprentissage de façon correcte. Cependant, des différences existent entre ces quatre modèles. En effet, bien qu’ils soient égaux vis-à-vis des données d’apprentissage, ils n’ont...

Le SVM du point de vue analytique

L’objectif de l’algorithme SVM est de trouver l’hyperplan qui sépare en deux classes avec la marge maximale les données de la base d’apprentissage. Cette section montre la démarche analytique pour atteindre cet objectif.

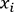Supposons que les deux classes à séparer sont la classe des exemples positifs et celle des exemples négatifs. Nous avons vu qu’une fois l’hyperplan séparateur trouvé, pour déterminer la classe d’appartenance d’un point , le SVM utilise une constante C et le vecteur 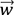, qui est un vecteur normal à l’hyperplan, comme suit :

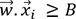Si , alors 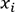est positif.

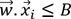Si , alors 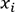est négatif.

Si nous remplaçons B par -b, nous obtenons :

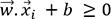, pour les futurs points 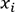positifs

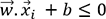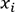, pour les futurs points négatifs

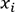Avec les deux inéquations précédentes, déterminer la classe d’un point revient à étudier le signe de la quantité 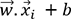. S’il est positif, alors 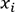appartient à la classe des points positifs, sinon il appartient à la classe des points négatifs. En résumé, la classe d’un point 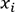est déterminée par :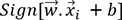

(1)

Données non linéairement séparables

Jusqu’à présent, dans ce chapitre, l’algorithme SVM tel qu’il a été présenté traite uniquement des données linéairement séparables. Ainsi, la figure 11-2 a montré que pour trouver la classe d’appartenance d’un nouveau point, le modèle SVM procède à la projection de ce point sur l’axe portant le vecteur normal de l’hyperplan qui sépare linéairement les données de la base d’entraînement.

Dans la plupart des problèmes posés dans la vraie vie, les données sont rarement linéairement séparables. Pour contourner ce problème, il existe une solution consistant à appliquer une transformation sur les données.

L’idée de cette transformation est de passer par un espace intermédiaire dans lequel les données sont linéairement séparables et dans lequel le SVM peut être appliqué exactement comme l’ont montré les sections précédentes, puis restituer les résultats dans l’espace d’origine.

La figure suivante donne un exemple très simple de données non linéairement séparables. En effet, aucune droite ne peut séparer correctement les cercles d’un côté et les triangles de l’autre côté.

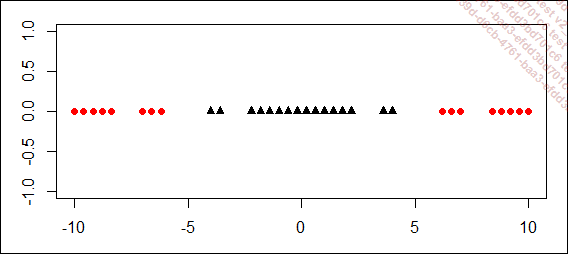
Figure 11-5 : exemple de données non linéairement séparables

Détecter les fraudes de cartes de crédit

Cet exemple concerne la réalisation d’un modèle pour détecter les fraudes de cartes de crédit. Il s’agit d’entraîner un modèle sur un ensemble de données contenant des transactions saines et des transactions frauduleuses.