Arithmétique et cryptographie
La division euclidienne des entiers
Les premières recherches sur la divisibilité des nombres entiers ont été menées par Pythagore et ses disciples. Elles ont été poursuivies et enrichies par Euclide.
1. Deux fonctions de Python
Si a et b sont deux entiers naturels avec b≠0, il existe deux entiers uniques q et r tels que a=qb+r avec 0 ≤ r < b. Les nombres q et r sont respectivement le quotient euclidien de a par b et le reste de la division euclidienne de a par b. Python dispose des opérateurs // et % pour calculer respectivement q et r. Le petit programme qui suit utilise ces deux fonctions pour calculer ces deux nombres.
# Quotient et reste euclidiens de 2 entiers naturels
a=eval(input("Valeur de a ?"))
b=eval(input("Valeur de b ?"))
q=a//b
r=a%b
print("quotient euclidien : ",q)
print("reste euclidien : ",r) Par exemple 30// 4 renvoie le quotient 7 et 30%4 renvoie le reste 2.
2. La division euclidienne des entiers relatifs
La division euclidienne définie dans N peut être étendue sans difficultés à Z mais sa définition doit être légèrement modifiée. Si a et b sont deux entiers relatifs, avec b ≠ 0, on démontre qu’il existe un seul entier relatif q et un seul entier naturel r tels que a=qb+r avec 0 ≤ r < |b|.
Le programme suivant, qui utilise également les fonctions // et %, calcule le quotient et le reste euclidiens dans la division euclidienne d’un nombre relatif a par un nombre relatif b non nul.
# Division euclidienne dans Z
a=eval(input("Choisir a : "))
b=eval(input("Choisir b : "))
if a>=0 and b>0:
q=a//b
r=a%b
if a>=0 and b<0:
q=-(a//(-b)) ...Les diviseurs d’un entier naturel
De Pythagore à Euclide, la recherche des diviseurs d’un entier naturel a donné lieu à de nombreuses recherches comme, par exemple, celle des nombres parfaits ou encore celle des nombres amicaux. Ces recherches ont été poursuivies ensuite par de nombreux mathématiciens dont Fermat et Euler.
1. Recherche des diviseurs d’un entier naturel
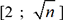 . En effet,
si
. En effet,
si 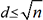 divise n et
n’est pas un carré parfait, le nombre
divise n et
n’est pas un carré parfait, le nombre  est aussi un diviseur de n mais
est supérieur à
est aussi un diviseur de n mais
est supérieur à 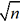 . Le programme ci-dessous tire parti de cette
remarque qui permet de calculer les diviseurs d’un entier naturel
par groupes de 2.
. Le programme ci-dessous tire parti de cette
remarque qui permet de calculer les diviseurs d’un entier naturel
par groupes de 2.# Liste des diviseurs d'un entier naturel n
from math import *
n=eval(input("Choisissez un entier plus grand que 1 : "))
nombrediviseurs=2
d=2
# d=2 est le premier diviseur de n possible
dr=0
# dr est un drapeau qui vaut 0 tant que d ne divise pas n
print("Liste des diviseurs :)
print ("1 et ", n)
while d<=sqrt(n):
r=n%d
# On cherche le reste de la division euclidienne de n par d
if r==0 and d!=sqrt(n) :
print(d, " et ", n//d)
dr=1
# dr=1 quand d divise n
nombrediviseurs=nombrediviseurs+2
elif r==0 and d==sqrt(n) :
# Si n est un carré, sqrt(n) est un diviseur de n ;
print(d)
nombrediviseurs=nombrediviseurs+1 ...Les nombres premiers
Dans le livre VII de ses Éléments, Euclide qualifie de « premier » un nombre entier qui n’est « mesuré que par la seule unité ». Quand il est mesuré par un autre nombre que l’unité, il n’est pas premier mais est composé.
1. Les nombres premiers sont en nombre infini
Euclide a démontré qu’il existe une infinité de nombres premiers. Dans le journal Le Monde, daté du 10 février 2016, le mathématicien Étienne Ghys expose ainsi le principe de la démonstration d’Euclide : « Considérons les nombres premiers 5, 13 et 31. Aucun d’entre eux ne divise le nombre 5x13x31+1=2016. Les diviseurs premiers de 2016 sont donc différents de ceux dont on est parti. Donc, pour toute liste finie de nombres premiers, on peut trouver un nombre premier qui n’est pas dans la liste. ».
2. Le crible d’Ératosthène
Ératosthène (276-194), mathématicien, astronome et géographe grec, est resté célèbre pour avoir calculé de façon précise le rayon de la Terre. Il est aussi l’inventeur d’une méthode, le « crible » d’Ératosthène, utilisée pour rechercher les nombres premiers.
Pour rechercher par exemple les nombres premiers inférieurs à 100, il commence par construire un tableau qui présente les nombres de 1 à 100. Il élimine ensuite 1 et tous les entiers pairs, puis tous les multiples de 3, puis tous les multiples de 5 et ainsi de suite. À la fin, il ne reste plus dans le tableau que les nombres premiers.
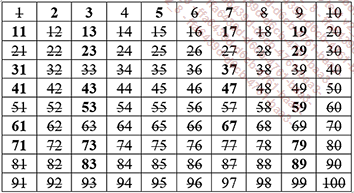
3. Comment savoir si un entier donné est premier ?
Le PGCD de deux entiers
Euclide définit deux entiers qui sont premiers entre eux comme des entiers dont « la plus grande commune mesure vaut 1 ». Si deux entiers ne sont pas premiers entre eux, c’est qu’ils ont plusieurs diviseurs communs et l’un d’entre eux, le PGCD, est le plus grand de tous.
1. L’algorithme d’Euclide
Soient a et b deux entiers naturels tels que a ≥ b. Pour calculer leur PGCD, Euclide utilisait un algorithme basé sur le calcul successif de plusieurs soustractions. Après avoir calculé a - b = d, on remplace a par le plus grand des deux nombres b et d et on fait la soustraction. On recommence de la même façon jusqu’à obtenir un résultat égal à 0. On obtient alors le PGCD des deux nombres.
Calculons par exemple le PGCD de 90 et de 36 avec cette méthode. On obtient successivement 90-36=54, 54-36=18 et enfin 18-18=0. Le PGCD de 90 et de 36 est donc 18.
# Calcul d'un PGCD par différences successives
a=eval(input("Valeur de a ?"))
b=eval(input("Valeur de b ?"))
while a!=b:
d=abs(b-a)
b=a
a=d
print("pgcd=",d)
if d==1:
print("Les deux entiers sont premiers entre eux.") 2. La méthode des divisions successives
On utilise aujourd’hui une forme modernisée de l’algorithme d’Euclide. Au lieu d’effectuer des soustractions en cascade, on effectue des divisions euclidiennes successives. Pour obtenir par exemple le PGCD de 753 et de 246, on effectue quatre divisions dont les résultats sont présentés dans le tableau suivant :
|
Rang de la division |
Dividende D |
Diviseur d |
Reste r |
|
1 |
753 |
246 |
15 |
|
2 |
246 |
15 |
6 |
|
3 |
15 |
6 |
3 |
|
4 |
6 |
3 |
0 |
Le PGCD cherché...
Les factorisations d’un entier naturel
Dans le livre VII de ses Éléments, Euclide démontre que tout nombre entier plus grand que 1 est divisible par un nombre premier. Il en résulte que chaque entier naturel peut être écrit comme un produit de nombres premiers d’une façon unique, à l’ordre près.
1. Décomposition en facteurs premiers
Soit n un entier naturel quelconque. Pour le décomposer en un produit de facteurs premiers, on commence par essayer de le diviser autant de fois qu’il est possible par 2. Chaque fois qu’une division est possible, on affiche 2 et on remplace n par le quotient euclidien n//2. Une fois toutes les divisions par 2 « épuisées », on passe aux divisions par 3, puis par 4, puis par 5, puis par 6 et ainsi de suite. Comme toutes ces divisions successives sont « épuisées » au fur et à mesure de l’avancée du programme, les nouvelles valeurs de n ne sont pas divisibles par les multiples de 2, de 3, de 4, de 5, etc. Finalement, seules les divisions possibles et répétées par les nombres premiers de l’intervalle [1;n] sont prises en compte. On utilise en quelque sorte une variante moderne du crible d’Ératosthène qui rayait successivement dans un tableau de nombres les multiples de 2, de 3, de 5, etc. À la fin, il ne reste plus que les nombres premiers. Le programme est le suivant :
# Décomposition de l'entier n en un produit de facteurs
# premiers entre eux
n=eval(input("Entrez l'entier n : "))
d=2
while n>1:
while n%d==0:
n=n//d
print(d)
d=d+1 Avec n=32480, on obtient 2×2×2×2×2×5×7×29...
Le théorème de Bezout
Soient a et b deux entiers relatifs. Le théorème de Bezout permet de répondre aux deux questions suivantes : existe-t-il des entiers relatifs u et v qui vérifient l’équation au+bv=pgcd(a,b) ? Si oui, u et v sont-ils uniques ?
1. Historique
La première formulation de ce théorème est due au mathématicien et poète Claude Gaspard Bachet de Méziriac (1581-1638) qui en donne une démonstration dans la seconde édition de son ouvrage Problèmes plaisants et délectables qui se font par les nombres paru en 1624. Le théorème est complété au XVIIIe siècle par Étienne Bezout (1730-1783).

Etienne Bezout (1730-1783)
2. Deux exemples
La recherche des nombres u et v peut se faire en utilisant l’algorithme d’Euclide appliqué aux nombres a et b. Il faut exprimer les restes des divisions euclidiennes successives en fonction de a et de b en utilisant l’algorithme d’Euclide.
1. Prenons comme premier exemple deux nombres a=136 et b=96 qui ne sont pas premiers entre eux. Le détail des calculs est présenté dans le tableau suivant :
|
136=1×96+40 |
40=136-96=a-b |
|
96=2×40+16 |
16=96-2×40=b-2(a-b)= 3b-2a |
|
40=2×16+8 |
8=40-2×16=(a-b)-2(3b-2a)= 5a-7b |
|
16=2×8+0 |
|
On obtient pgcd(136,96)=8=5×136-7×96. Les nombres 5 et -7 sont appelés des coefficients de Bezout. :
2. Dans le deuxième exemple, nous prendrons a=135 et b=56 qui sont premiers entre eux. On a successivement :
|
135=2×56+23 |
23=135-2×56=a-2b |
|
56=2×23+10 |
10=56-2×23=b-2(a-2b)= 5b-2a |
|
23=2×10+3 |
3=23-2×10=(a-2b)-2(5b-2a)= 5a-12b |
|
10=3×3+1 |
1=10-3×3=(5b-2a)-3(5a-12b)=-17a+41b |
|
3=3×1+0 |
|
On obtient pgcd (135,56)=1=-17×135+41×56. Les nombres -17 et 41 sont appelés des...
Introduction aux équations diophantiennes
Une équation diophantienne est une équation à plusieurs inconnues et à coefficients entiers. Les solutions de ces équations doivent également être des nombres entiers.
1. Historique
Diophante a vécu à Alexandrie entre le Ier siècle avant J.-C. et le IVe siècle après J.-C. Contrairement aux autres mathématiciens grecs qui étaient très préoccupés de géométrie, il a étudié essentiellement les propriétés des nombres entiers et a écrit un traité d’arithmétique. Bien qu’elle n’ait pas été transmise en totalité, son œuvre a influencé de nombreux mathématiciens, d’abord arabo-musulmans puis européens. Les fragments de ses ouvrages qui nous sont parvenus ont été traduits en latin par le français Claude-Gaspard Bachet de Méziriac (1581-1638) au XVIIe siècle.

Bachet de Méziriac
2. Un exemple d’équation diophantienne
Dans un recueil de récréations mathématiques qui s’intitule Problèmes plaisants et délectables qui se font par les nombres, Bachet de Méziriac propose des problèmes qui reposent sur des équations diophantiennes. Par exemple, le problème X de cet ouvrage est le suivant : « Il y a 41 personnes en un banquet tant hommes que femmes et enfants qui en tout dépensent 40 sous, mais chaque homme paye 4 sous, chaque femme 3 sous, chaque enfant 4 deniers (1 2 deniers =1 sou). Je demande combien il y a d’hommes, combien de femmes et combien d’enfants. »
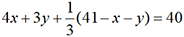 qui, après simplification, peut encore
s’écrire...
qui, après simplification, peut encore
s’écrire...La congruence des entiers relatifs
Cette notion a été proposée par Gauss (1777-1855) au tout début du XIXesiècle. Elle est aujourd’hui couramment utilisée en théorie des nombres et en cryptographie. Elle est la base de ce qu’on appelle l’arithmétique modulaire.

Carl-Friedrich Gauss
1. Le terme « modulo »
Si n est un entier naturel non nul, on dit que deux entiers relatifs a et b sont congrus modulo n s’ils ont le même reste euclidien quand on les divise par n. On écrit alors a ≡b [n] ou encore a = b [modulo n].
Exemple : quand on divise 14 et 17 par 3, on obtient un reste égal à 2, donc 14 ≡ 17 [3].
« Modulo » vient du latin « modulus » qui signifie « mesure ». Modulo 26 signifie « selon le module 26 ». « Congru » provient également du verbe latin « congruere », « s’accorder ».
2. Calcul des restes modulo n
Soit z un entier relatif et soit n un entier naturel non nul. Le reste de la division euclidienne de z par n est un entier naturel r tel que 0 ≤ r <n. À titre d’exemple, cherchons le reste de la division euclidienne de -155 par 9. On a 155=17×9+2 d’où -155=-17×9-2. Comme 2=9-7, on peut écrire -155=-17×9-(9-7) d’où -155=-18x9+7. Le reste cherché est 7. En utilisant la même méthode que dans l’exemple, on peut calculer le reste euclidien de la division de z par n.
# Reste modulo n d'un entier relatif z
z=eval(input("Choisissez l'entier relatif z :"))
n=eval(input("Choisissez l'entier naturel n :"))
if z>=0:
r=z%n
else: ...Le code secret de Jules César
La cryptologie, étymologiquement la science du secret, existe depuis longtemps. Elle présente deux aspects bien distincts : la cryptographie, qui étudie l’ensemble des techniques qui permettent de coder un message, et la cryptanalyse, qui essaye de décoder les messages codés. Cette discipline entretient évidemment des liens étroits avec les mathématiques, l’informatique et la linguistique.
1. Historique
Dans Les vies des douze César, Suétone rapporte que, pendant la conquête des Gaules, Jules César communiquait avec ses généraux grâce à un code secret qu’il avait imaginé. La technique en est particulièrement simple : il suffit de procéder à une permutation circulaire des lettres de l’alphabet en remplaçant chaque lettre par celle qui est située trois rangs après elle : D remplace A, E remplace B, F remplace C et ainsi de suite jusqu’à la lettre Z qui est remplacée par la lettre C.
Par exemple, VENI VIDI VICI devient YHQLYLGLYLFL.
2. Les instructions ord() et chr() de Python
Chaque caractère imprimable par un ordinateur est associé à un nombre entier compris entre 32 et 255 qu’on appelle code ASCII. Pour coder un texte, par quelque méthode que ce soit, il nous faudra utiliser deux instructions du langage Python. L’instruction ord(caractère) renvoie le code ASCII du caractère indiqué.
print("Choisissez une lettre quelconque :")
lettre=input()
code=ord(lettre)
print("Code de la lettre choisie=",code) Inversement l’instruction chr(n) renvoie le caractère imprimable dont le code ASCII est l’entier n, pourvu que n soit compris entre 32 et 255. Cependant, le code ASCII d’une lettre capitale non accentuée...
Le chiffre de Vigenère
Le principe de cette méthode de codage consiste à utiliser un décalage différent pour chaque lettre du texte à coder. Contrairement à celle de Jules César, cette méthode offre une bonne résistance aux analyses de fréquences, puisqu’elle n’a été « cassée » qu’en 1854 par Charles Babbage (1791-1871).
1. Historique
Le service du chiffre des rois de France s’est développé dans la seconde moitié du XVIe siècle. Le mathématicien François Viète entre en 1576 au service du roi Henri III puis, à la mort d’Henri III, devient le déchiffreur du roi Henri IV. En septembre 1589, usant d’analyses statistiques et de méthodes qu’il se garde de publier, François Viète parvient à casser les codes des lettres secrètes espagnoles. À partir de 1594, il est chargé exclusivement du décryptage des codes secrets ennemis. Apprenant qu’il a décrypté leurs lettres secrètes, les Espagnols l’accusent de sorcellerie.
 Blaise de Vigenère (1523-1596) |
 François Viète (1540-1603) |
Blaise de Vigenère (1523-1596), qui a d’abord été diplomate au service de Henri III, a lui aussi été un spécialiste du chiffre. En 1586, il a publié un Traité des Chiffres dans lequel il décrit un chiffrement à clé de son invention. C’est le premier chiffrement de ce genre, chiffrement qui s’est révélé très difficile à casser.
2. Principe du chiffre de Vigenère
Codons par exemple le texte CECI EST SECRET et prenons pour clé le mot LUNE. Cette clé va définir le décalage qui sera appliqué à chaque lettre...
Les codages affines
Le codage affine généralise la méthode de Jules César. Il transforme chaque lettre de l’alphabet en une autre lettre de l’alphabet à l’aide d’une fonction affine.
1. Une convention
Pour simplifier les choses, convenons de ne prendre que des lettres capitales non accentuées et choisissons deux nombres entiers a et b dans l’intervalle [0 ; 25]. Soit x le rang d’une lettre quelconque de l’alphabet et soit y celui de sa transformée. Par définition, le nombre y est le reste de la division euclidienne du nombre ax+b par 26.
2. Un programme pour coder un texte
Le programme suivant permet le codage affine d’un texte écrit en lettres capitales non accentuées et dépourvu d’espaces.
# Codage affine d'un texte
print("Quelle phrase voulez-vous coder ?")
x=input()
n=len(x)
a=eval(input("Choisissez un entier a :"))
b=eval(input("Choisissez un entier b :"))
nouveautexte=""
for i in range(0,n):
y=ord(x[i])
y=65+((a*y+b)-65)%26
nouveautexte=nouveautexte+chr(y)
print("Voici le texte codé :", nouveautexte) Codons par exemple le texte VENI VIDI VICI de Jules César en prenant a=9 et b=5. Le texte codé est le suivant :
Quelle phrase voulez-vous coder ?
VENIVIDIVICI
Choisissez un entier a : 9
Choisissez un entier b : 5
Voici le texte codé : MPSZMZGZMZXZ Voici le codage du même texte pour a=20 et b=12 :
Quelle phrase voulez-vous coder ?
VENIVIDIVICI
Choisissez un entier a : 20
Choisissez un entier b : 12
Voici le texte codé : DBZDDDHDDDND 3. Comment choisir les entiers a et b ?
Parmi les valeurs possibles de a et de b, toutes ne conviennent...
Le chiffrement de Hill
Lester S. Hill (1891-1961) est un mathématicien américain qui s’est intéressé à la détection des erreurs dans les communications et à la cryptologie. En 1929, il a inventé une nouvelle méthode de chiffrement et conçu une machine capable de réaliser les codages mécaniquement.
1. Principe du chiffrement
Le procédé imaginé par Hill consiste à regrouper dans un premier temps les lettres 2 par 2. On remplace ensuite les deux lettres de chaque groupe par leurs rangs dans l’alphabet. Chacun de ces couples de nombres est remplacé à son tour par deux autres couples de nombres calculés modulo 26 à l’aide d’une matrice de chiffrement carrée de taille 2x2. Cette méthode de codage rend beaucoup plus difficile le décryptage d’un texte codé à partir de l’observation des fréquences de ses lettres.
2. Un exemple
Pour coder un texte ne comprenant que des lettres, on écrira ces lettres en lettres capitales. Codons par exemple le nom de JULES CESAR.
On découpe le texte écrit en clair en groupes de deux lettres sans tenir compte des espaces : JU LE SC ES AR. Après avoir numéroté les lettres de l’alphabet de 0 à 25, on écrit les rangs de chaque lettre du message.

On choisit ensuite une matrice carrée de codage de taille 2×2 dont les coefficients sont des nombres de l’ensemble Z/26. Cette matrice doit être inversible18 car son inverse sera utilisée pour déchiffrer les messages codés mais, pour éviter le calcul de l’inverse modulo 26 d’une matrice carrée, nous choisirons uniquement des matrices dont le déterminant est égal à 1 et nous en choisirons les coefficients dans l’intervalle [0;25]....
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

