Matrices 2x2 et matrices 3x3
Matrices carrées et applications linéaires
Dans l’histoire des mathématiques, les tableaux de nombres sont apparus très tôt, en Chine par exemple, avec la résolution des systèmes d’équations du premier degré. Par contre, le calcul matriciel proprement dit n’est apparu qu’au XIXe siècle avec la théorie des déterminants.
1. Historique
Le mot « matrice » est la traduction du terme « matrix » fabriqué en 1850 par J.J. Sylvester (1814-1897) à partir du mot latin « mater ». En 1854, Arthur Cayley (1821-1895) associe les matrices aux applications linéaires en écrivant que les matrices sont une « notation commode pour représenter les fonctions linéaires ». Il définit également les opérations usuelles du calcul matriciel, l’addition, la multiplication et le produit par un scalaire. Le nouveau calcul va s’appliquer assez vite aux vecteurs qui viennent d’être définis par H. Grassmann (1809-1877). Comme les premières études concernent surtout le plan et l’espace, on ne considère au début que des matrices carrées d’ordre 2 ou 3. Hamilton (1805-1865) est le premier qui envisage des matrices 4×4 mais ce n’est qu’à la fin du XIXe siècle que l’on étudie des matrices dont les dimensions sont beaucoup plus grandes.
L’habitude de noter les matrices avec des crochets ou des parenthèses date de 1913. La notation qui consiste à désigner par aij le terme situé sur la ie ligne et sur la je colonne date de la même époque. L’algèbre linéaire devient une discipline à part entière en 1888 quand le mathématicien italien G. Peano...
Opérations sur les matrices
Les matrices carrées représentent des applications linéaires d’un espace vectoriel E dans lui-même. Puisqu’on peut additionner et composer des applications linéaires, on pourra additionner, soustraire et multiplier des matrices carrées.
1. Addition, soustraction et multiplication par un réel
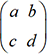 et
et 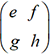 les matrices qui leur sont associées. Il
est facile de voir que la matrice associée à l’application f+g est
les matrices qui leur sont associées. Il
est facile de voir que la matrice associée à l’application f+g est 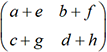 tandis que celle qui est associée à l’application f-g est
tandis que celle qui est associée à l’application f-g est 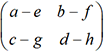 . Ainsi, pour
. Ainsi, pour 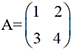 et
et 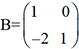 , on aura
, on aura 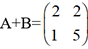 et
et 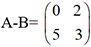 .
.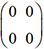 est la matrice nulle. Quelle que soit la matrice
est la matrice nulle. Quelle que soit la matrice 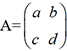 , on a
, on a 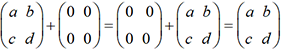 .
.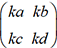 représente l’application linéaire kf définie par
représente l’application linéaire kf définie par 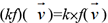 . Multiplions par exemple la matrice
. Multiplions par exemple la matrice 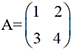 par 3 à l’aide du petit programme suivant :
par 3 à l’aide du petit programme suivant :# Produit d'une matrice 2x2 par un réel k
A=[[1,2],[3,4]]
k=3
P=[[0,0],[0,0]]
for i in range(0,2):
# i prend donc successivement les valeurs 0 et 1
for j in range(0,2):
# j prend successivement les valeurs 0 et 1
P[i][j]=k*A[i][j]
print("P=",k,"A=",P) Dans les instructions for i in range(0,2): et for j in range(0,2):, les nombres entiers i et j prennent 0 et 1 comme valeurs. Le résultat est le suivant :
P=3A= [[3, 6], [9, 12]] 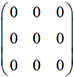 est la matrice nulle.
est la matrice nulle.2. Multiplication des matrices carrées de taille 2
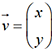 par f,
par g, par gof et par fog,
on constate que
par f,
par g, par gof et par fog,
on constate que 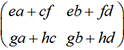 et
et 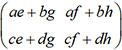 sont...
sont...Déterminant d’une matrice carrée 2x2 ou 3x3
L’étude théorique des déterminants trouve son origine dans la résolution des systèmes d’équations linéaires. Au XIXe siècle, Gauss (1789-1857) associe l’étude des déterminants d’ordre 3 à celle des applications linéaires de E3 dans E3, mais c’est Cauchy (1789-1857) qui donne la définition la plus générale du déterminant d’une matrice.

Augustin Louis Cauchy (1789-1857)
1. Déterminant d’une matrice 2x2
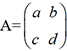 est le nombre égal à ad-bc et
noté
est le nombre égal à ad-bc et
noté 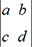 ou det(A).
ou det(A).Cette notation est due à Arthur Cayley (1821-1895).
On peut le calculer avec le programme qui suit.
# Calcul du déterminant d'une matrice de taille 2x2
from math import*
def det(a,b,c,d):
return a*d-b*c
# Entrée des coefficients de la matrice A
a,b=eval(input("Entrez a11 et a12 : "))
c,d=eval(input("Entrez a21 et a22 : "))
# Calculs et résultats
D=det(a,b,c,d)
print("Le déterminant de la matrice est égal à ",D)  est -2.
est -2.Entrez a11 et a12 : 1,2
Entrez a21 et a22 : 3,4
Le déterminant de la matrice est égal à -2  est égal à 2 × 5 = 10.
est égal à 2 × 5 = 10.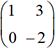 et
et 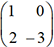 dont les déterminants sont égaux
au produit de leurs éléments diagonaux, c’est-à-dire
-2 et -3 respectivement.
dont les déterminants sont égaux
au produit de leurs éléments diagonaux, c’est-à-dire
-2 et -3 respectivement.2. Déterminant d’une matrice 3x3
 une matrice...
une matrice...Inversion des matrices carrées 2x2 et 3x3
Plusieurs méthodes différentes permettent de calculer l’inverse d’une matrice carrée ayant n2 coefficients. Pour n=2 ou n=3, il est assez commode d’employer les méthodes de calcul du mathématicien et astronome Pierre-Simon de Laplace (1749-1827) qui utilisait des déterminants. Par contre, pour n>3, il faut recourir à d’autres méthodes.

Pierre-Simon de Laplace
1. Qu’est-ce qu’une matrice inversible ?
On dit qu’une matrice carrée A est inversible s’il existe une matrice notée A-1 telle que A×A-1=A-1×A=Id. On démontre que A est inversible si et seulement si son déterminant n’est pas nul.
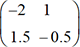 est l’inverse de
est l’inverse de 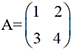 .
.2. Inverse d’une matrice carrée 2x2
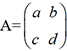 une matrice
inversible dont le déterminant det(A)=ad-bc n’est pas
nul. A est donc inversible. Laplace a montré que
une matrice
inversible dont le déterminant det(A)=ad-bc n’est pas
nul. A est donc inversible. Laplace a montré que 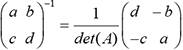 . Dans quelques cas particuliers, il est facile
de former l’inverse d’une matrice carrée de taille 2. Ainsi,
l’inverse d’une matrice diagonale de la forme
. Dans quelques cas particuliers, il est facile
de former l’inverse d’une matrice carrée de taille 2. Ainsi,
l’inverse d’une matrice diagonale de la forme 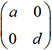 est une matrice diagonale
est une matrice diagonale 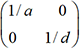 .
.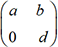 est la matrice
triangulaire de la forme
est la matrice
triangulaire de la forme 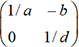 . Notons
. Notons 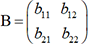 , quand elle existe, la matrice inverse d’une
matrice carrée
, quand elle existe, la matrice inverse d’une
matrice carrée 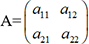 . Le programme
de calcul de B est le suivant :
. Le programme
de calcul de B est le suivant :# Inversion d'une matrice carrée A de taille 2
from math import*
# Entrée des coefficients de A
a,b=eval(input("Valeur de a11 et de a12 ? "))
c,d=eval(input("Valeur de a21 et de a22 ? "))
# Calculs et résultats
det=a*d-b*c
if abs(det)<0.001:
print("Matrice singulière.")
else:
L1=[d/det,-b/det]
L2=[-c/det,a/det] ...Résolution d’un système linéaire d’équations
L’étude et la résolution des systèmes de 2 équations du 1er degré à 2 inconnues est très ancienne, puisque les mathématiciens chinois étaient déjà capables de les résoudre deux siècles avant J.-C.
1. Un exemple historique
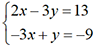 dans l’ancienne Chine, on
commençait par disposer des baguettes sur une table à calculer.
Des baguettes noires représentaient des nombres positifs
tandis que des baguettes rouges représentaient des nombres
négatifs. La méthode utilisée consistait à changer les
coefficients du système en utilisant des combinaisons de
lignes et de colonnes. Les calculs étaient choisis pour
faire apparaître d’abord un 0 dans la case située à l’intersection
de la ligne 2 et de la colonne 2 puis un 0 dans la case située à l’intersection
de la ligne 1 et de la colonne 1.
dans l’ancienne Chine, on
commençait par disposer des baguettes sur une table à calculer.
Des baguettes noires représentaient des nombres positifs
tandis que des baguettes rouges représentaient des nombres
négatifs. La méthode utilisée consistait à changer les
coefficients du système en utilisant des combinaisons de
lignes et de colonnes. Les calculs étaient choisis pour
faire apparaître d’abord un 0 dans la case située à l’intersection
de la ligne 2 et de la colonne 2 puis un 0 dans la case située à l’intersection
de la ligne 1 et de la colonne 1.Résolvons par cette méthode le système écrit quelques lignes plus haut en utilisant cependant nos propres notations.
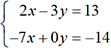 d’où on
tire
d’où on
tire 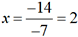 .
.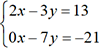 d’où on tire
d’où on tire 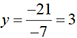 .
.Les mathématiciens chinois ont été les premiers à utiliser des tableaux de nombres pour résoudre des systèmes d’équations. En Europe, ils sont apparus pour la première fois en 1545 dans...
Puissances d’une matrice 2x2 ou 3x3
Puisqu’on peut multiplier des matrices, il est possible d’élever une matrice à une puissance 2, 3 ou plus. Pour n≥1, An est le produit de n matrices toutes égales à A. Pour n=0, A0 est égale à la matrice unité. Dans ce qui suit, nous n’utiliserons que des matrices carrées.
1. Puissance d’une matrice 2x2
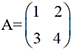 une matrice
carrée d’ordre 2. Proposons-nous de calculer An pour n entier positif. On peut utiliser
le programme suivant :
une matrice
carrée d’ordre 2. Proposons-nous de calculer An pour n entier positif. On peut utiliser
le programme suivant :# Puissance d'une matrice 2x2
from math import*
# Entrée des données
a,b=eval(input("Coefficients de la 1ère ligne : "))
c,d=eval(input("Coefficients de la 2ème ligne : "))
n=eval(input("Valeur de l'exposant ?"))
# Calculs et résultats
A1,B1,C1,D1=1,0,0,1
for i in range(0,n):
A2=A1*a+B1*c
B2=A1*b+B1*d
C2=C1*a+D1*c
D2=C1*b+D1*d
A1,B1,C1,D1=A2,B2,C2,D2
M=[[A1,B1],[C1,D1]]
print("Résultat du calcul :", M) 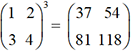 .
.Coefficients de la 1re ligne : 1,2
Coefficients de la 2e ligne : 3,4
Valeur de l'exposant ? 3
Résultat du calcul : [[37, 54], [81, 118]] 2. Puissance d’une matrice 3x3
Si A est une matrice carrée d’ordre 3, en modifiant un peu le programme précédent, on pourra calculer une puissance nième An pour n entier positif.
# Puissance d'une matrice 3x3
from math import*
# Entrée des données
a,b,c=eval(input("Entrer les 3 coefficients de la 1re ligne : "))
d,e,f=eval(input("Entrer les 3 coefficients de la 2e ligne : "))
g,h,i=eval(input("Entrer les 3 Coefficients...Diagonalisation d’une matrice 2x2
Dans certains cas, il peut y avoir une relation simple entre les puissances nièmes de deux matrices 2×2 différentes A et B. Au lieu de calculer An, il peut alors s’avérer plus simple de calculer Bn.
1. Les matrices diagonisables
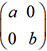 , on a A=PBP-1 et An=PBnP-1.
On dit que A est une matrice diagonalisable. La puissance nième de
A est alors beaucoup plus simple à calculer puisque
, on a A=PBP-1 et An=PBnP-1.
On dit que A est une matrice diagonalisable. La puissance nième de
A est alors beaucoup plus simple à calculer puisque 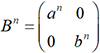 .
.2. Étude d’un exemple
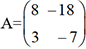 . Cherchons une matrice
. Cherchons une matrice 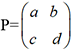 et une matrice
et une matrice 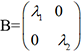 telles que
telles que 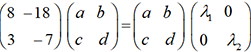 . Cette recherche nécessite la détermination,
si elles existent, des valeurs propres de
. Cette recherche nécessite la détermination,
si elles existent, des valeurs propres de 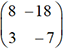 et des vecteurs propres qui lui sont associés.
et des vecteurs propres qui lui sont associés. et
et 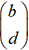 différents
de
différents
de 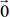 et supposons les nombres λ1 et λ2 non
nuls. Dans ces conditions, on peut observer que
et supposons les nombres λ1 et λ2 non
nuls. Dans ces conditions, on peut observer que 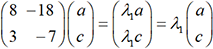 et que
et que 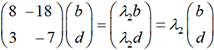 . L’équation AX=λX a
des solutions en λ et
en X. On dit qu’une valeur
de λ qui
est solution de cette équation est une valeur propre de
la matrice A et qu’un vecteur X qui est solution de cette équation
est un vecteur propre associé à une certaine valeur propre λ.
. L’équation AX=λX a
des solutions en λ et
en X. On dit qu’une valeur
de λ qui
est solution de cette équation est une valeur propre de
la matrice A et qu’un vecteur X qui est solution de cette équation
est un vecteur propre associé à une certaine valeur propre λ.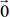 aurait alors plusieurs antécédents.
La matrice A-λI
n’est donc pas inversible...
aurait alors plusieurs antécédents.
La matrice A-λI
n’est donc pas inversible...Matrices et suites récurrentes
La suite (un) définie par ses deux premiers termes et par la relation de récurrence un+2 = aun+1 + bun est une suite récurrente d’ordre 2 à coefficients constants. Pour exprimer explicitement le terme de rang n, on peut utiliser une matrice carrée d’ordre 2.
1. Rappel : les nombres de Fibonacci
Pour tout entier naturel n, les nombres de Fibonacci F0, F1, F2, etc. sont définis par la relation de récurrence Fn+2=Fn+1+Fn avec F0=F1 =1.
2. Calcul des nombres de Fibonacci à l’aide d’une matrice 2x2
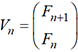 avec
avec 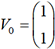 . Si M est la matrice
. Si M est la matrice 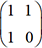 , on a alors Vn+1=MVn pour tout
entier naturel n d’où, par
récurrence sur n,
Vn=MnV0.
En adaptant le programme qui permet d’élever une matrice
carrée à la puissance n,
on peut utiliser cette relation de récurrence pour écrire
un programme qui calculera les n premiers
nombres de Fibonacci.
, on a alors Vn+1=MVn pour tout
entier naturel n d’où, par
récurrence sur n,
Vn=MnV0.
En adaptant le programme qui permet d’élever une matrice
carrée à la puissance n,
on peut utiliser cette relation de récurrence pour écrire
un programme qui calculera les n premiers
nombres de Fibonacci.from math import*
# Coefficients de la matrice M
a,b,c,d=1,1,1,0
liste=[]
n=eval(input("Valeur de n ? "))
# Calcul de Mn et affichage des résultats
A1,B1,C1,D1=1,0,0,1
for i in range(0,n):
A2=A1*a+B1*c
B2=A1*b+B1*d
C2=C1*a+D1*c
D2=C1*b+D1*d
A1,B1,C1,D1=A2,B2,C2,D2
liste=liste+[C1]
print(liste) Pour n=12, on obtient la liste [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144].
3. Les relations de Binet
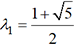 et
et 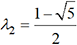 de son polynôme caractéristique λ2 - λ -
1 = 0. Une fois calculés les vecteurs
propres qui sont associés aux valeurs propres, on obtient
(avec Python...
de son polynôme caractéristique λ2 - λ -
1 = 0. Une fois calculés les vecteurs
propres qui sont associés aux valeurs propres, on obtient
(avec Python... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

