Résolution approchée des équations
La recherche d’une solution par dichotomie
Si on sait que l’équation f(x)=0 a une solution unique r dans un intervalle [a;b], cette méthode de recherche de r consiste à partager l’intervalle [a;b] en deux puis à repérer dans quelle partie se trouve le zéro recherché. On répète alors le processus autant de fois qu’il est nécessaire pour atteindre la précision souhaitée.
1. Historique
Né à Prague, le mathématicien
autrichien Bernhard Bolzano (1781-1848) s’est intéressé à la
théorie des fonctions d’une variable réelle. C’est
dans ce cadre qu’il a défini la continuité d’une
fonction, d’une façon presque équivalente à celle
qui sera donnée plus tard par Cauchy (1789-1857). Pour
Bolzano, une fonction f définie
sur un intervalle I « est continue en 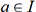 si et seulement si la quantité f (a+h) - f (a) peut être rendue plus petite que toute grandeur donnée si l’on peut toujours prendre h aussi petit que l’on voudra ».
Au lieu de s’appuyer sur l’évidence graphique, il s’est
appuyé sur cette définition pour donner une démonstration
rigoureuse du théorème des valeurs intermédiaires : « Si une fonction est continue sur un intervalle et prend deux valeurs m et n, alors elle prend toutes les valeurs comprises entre m et n ».
si et seulement si la quantité f (a+h) - f (a) peut être rendue plus petite que toute grandeur donnée si l’on peut toujours prendre h aussi petit que l’on voudra ».
Au lieu de s’appuyer sur l’évidence graphique, il s’est
appuyé sur cette définition pour donner une démonstration
rigoureuse du théorème des valeurs intermédiaires : « Si une fonction est continue sur un intervalle et prend deux valeurs m et n, alors elle prend toutes les valeurs comprises entre m et n ».
Bolzano en a tiré une conséquence importante exploitable par l’analyse numérique : si une fonction f est continue sur un intervalle [a;b] et si elle change de signe sur cet intervalle, alors elle s’annule en un point au moins de cet intervalle. Le théorème de Bolzano permet donc la recherche d’une...
La méthode des approximations successives
Dès que l’on s’est intéressé à des équations algébriques de degré supérieur à 3, on a essayé de les résoudre par des méthodes approchées. Depuis les travaux d’Evariste Galois, on sait qu’au-delà du quatrième degré, il ne peut plus exister de méthode exacte de résolution des équations. La méthode des approximations successives, appelée aujourd’hui méthode du point fixe, est l’une des plus anciennes méthodes de résolution approchée des équations.
1. Historique
Vers 1400, al-Kashi, astronome à l’observatoire de Samarkand, souhaitait construire une nouvelle table trigonométrique en calculant sin1° de façon précise en utilisant la relation sin3x = 3sin x - 4sin3 x. Pour calculer sin1°, al-Kashi devait résoudre l’équation sin3° = 3sin1°-4(sin1°)3. Le nombre sin3° se calcule facilement par étapes, à partir des valeurs remarquables déjà connues puisque, connaissant les lignes trigonométriques de 72° et de 60°, on en déduit celles de 12° puis, par deux divisions par 2 successives, on arrive aux lignes trigonométriques de 3°.
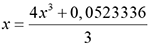 . Considérons alors la suite définie
par x1=0
et par
. Considérons alors la suite définie
par x1=0
et par 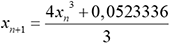 pour n≥ 1 Le programme qui suit
calcule les 25 premiers termes de cette suite.
pour n≥ 1 Le programme qui suit
calcule les 25 premiers termes de cette suite.# Le calcul de sin 1° par al-Kashi
def g(x):
return (4*x*x*x+0.0523336)/3 ...La méthode de Newton
En 1669, Newton publie De analysi per aequationes numero terminorum infinitas, un ouvrage dans lequel il explique comment résoudre des équations polynomiales de façon approchée.
Il expose sa méthode en traitant l’équation x3-2x-5=0.

Isaac Newton (1642-1727)
1. Historique
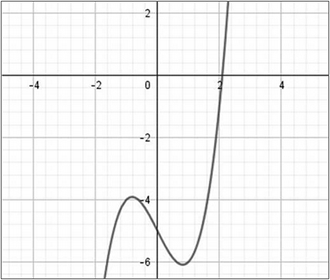
Refaisons les calculs de Newton en utilisant les notations et les moyens d’aujourd’hui. Une représentation graphique de la fonction x→x3-2x-5 permet de voir que l’équation x3-2x-5=0 admet une solution unique comprise entre 2 et 2,1.
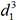 et
et 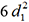 dans le résultat. L’équation P(x)=0
peut être remplacée par l’équation 10d1-1=0,
ce qui donne
dans le résultat. L’équation P(x)=0
peut être remplacée par l’équation 10d1-1=0,
ce qui donne 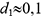 .
.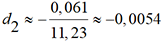 puis x3 = x2 + d2 = 2,1 - 0,0054 = 2,0946.
Le calcul peut être prolongé et d’autres approximations
peuvent être calculées.
puis x3 = x2 + d2 = 2,1 - 0,0054 = 2,0946.
Le calcul peut être prolongé et d’autres approximations
peuvent être calculées.2. Extension de la méthode
Le mathématicien anglais Thomas Simpson (1710-1761), connu surtout par sa méthode d’intégration numérique, a publié deux livres sur le nouveau calcul infinitésimal inventé par Newton....
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

