Calcul infinitésimal et intégration numérique
Longueur d’un arc de courbe
Le marquis de l’Hospital a publié en 1696 un traité intitulé Analyse des infiniment petits pour l’intelligence des lignes courbes. Ce livre marque les débuts du calcul infinitésimal. On peut y lire que « les lignes courbes doivent être considérées comme l’assemblage d’une infinité de lignes droites, chacune infiniment petite ».10

Guillaume de l’Hospital (1661-1704)
1. Principe du calcul
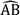 sur un intervalle [a;b]. Les
coordonnées de A sont a et f(a),
celles de B sont b et f(b).
sur un intervalle [a;b]. Les
coordonnées de A sont a et f(a),
celles de B sont b et f(b).
 de façon approchée, on peut
placer n points A2,
A3, …, An sur
cet arc entre A et B. On assimile alors la longueur de l’arc AB à la
somme des longueurs des segments A A2, A2 A3, …,
AnB.
de façon approchée, on peut
placer n points A2,
A3, …, An sur
cet arc entre A et B. On assimile alors la longueur de l’arc AB à la
somme des longueurs des segments A A2, A2 A3, …,
AnB. est remplacée
par la somme AA2+A2A3+A3A4+A4 A5+A5A6+A6B.
est remplacée
par la somme AA2+A2A3+A3A4+A4 A5+A5A6+A6B.2. Un programme de calcul
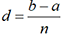 . Désignons par x1 l’abscisse
du point de subdivision Ai et
par x2 celle de Ai+1.
On a alors x1=a+id et x2=x1+d pour 0 ≤ i ≤ n.
. Désignons par x1 l’abscisse
du point de subdivision Ai et
par x2 celle de Ai+1.
On a alors x1=a+id et x2=x1+d pour 0 ≤ i ≤ n.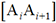 est égale à
est égale à 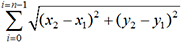 . Calculons par exemple la longueur L de l’arc de la parabole y=x2 ayant
pour extrémités les points d’abscisses a=0 et b=5.
. Calculons par exemple la longueur L de l’arc de la parabole y=x2 ayant
pour extrémités les points d’abscisses a=0 et b=5.# Calcul de la longueur d'un arc de parabole
from math import*
def f(x):
return x*x
a=eval(input("Valeur de l'abscisse du point A ?"))
b=eval(input("Valeur de l'abscisse du point B ?"))
n=eval(input("Valeur...Aire du disque et calcul de pi
Le calcul de l’aire du disque et la détermination de π ont été pendant bien longtemps au centre de l’activité des mathématiciens.
1. Historique
Un problème qui figure sur un papyrus rédigé par des scribes égyptiens nous explique la démarche qu’il faut suivre pour calculer l’aire d’un disque de diamètre 9 (l’unité n’est pas précisée). Voici cette méthode :
-
Prends
 du diamètre : cela fait 1 ;
le reste est 8.
du diamètre : cela fait 1 ;
le reste est 8. -
Fais la multiplication 8 fois 8 ; le résultat est 64.
-
L’aire est 64 sétats.
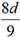 . Cela revient à calculer l’aire d’un
disque de rayon R avec la
formule
. Cela revient à calculer l’aire d’un
disque de rayon R avec la
formule 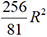 et à prendre π ≈ 3,16.
et à prendre π ≈ 3,16.2. Méthode d’Archimède
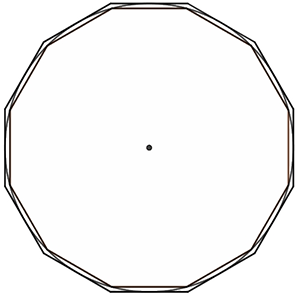
C’est dans un traité d’Archimède (287-212 avant J.-C.) intitulé La mesure du cercle qu’on trouve exposée la méthode qui lui a permis de calculer la longueur d’un cercle.

Statue d’Archimède
Le savant grec a utilisé les deux résultats suivants comme point de départ :
-
Le périmètre d’un polygone inscrit dans un cercle est toujours inférieur à la longueur du cercle.
-
Le périmètre d’un polygone circonscrit à un cercle est toujours supérieur à la longueur du cercle.
La figure qui suit illustre ces deux propositions dans le cas de deux dodécagones réguliers, l’un circonscrit au cercle, l’autre inscrit dans ce même cercle.
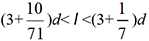 , ce qui constitue un excellent encadrement de
la longueur...
, ce qui constitue un excellent encadrement de
la longueur...Volume d’une boule
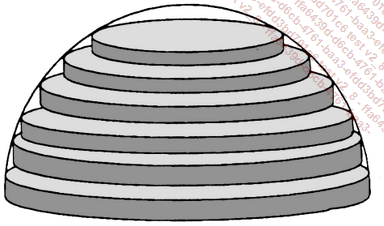
En remplaçant une boule par un empilement de cylindres droits de diamètres décroissants, il est possible d’obtenir un encadrement du volume de cette boule. Les calculs nécessaires reposent sur le théorème de Pythagore.
1. Principe du calcul
Au IIIe siècle avant J.-C., Archimède a réussi à calculer des aires et des volumes à l’aide de sa « méthode d’exhaustion ». Cette méthode consistait à remplacer le volume ou l’aire à évaluer par un très grand nombre de volumes ou d’aires plus simples, des rectangles, des prismes, des cylindres par exemple.
Avec la naissance du calcul infinitésimal, les mathématiciens du XVIIe siècle ont repris cette idée et l’ont appliquée à de nombreux cas, celui d’une boule par exemple.
2. Le calcul
En pratique, on peut se contenter d’effectuer les calculs pour une demi-boule seulement.
1. Le schéma qui suit montre comment on peut empiler des cylindres, 5 dans le cas de la figure, pour obtenir une valeur approchée par défaut du volume d’une demi-boule de rayon r et de centre O.
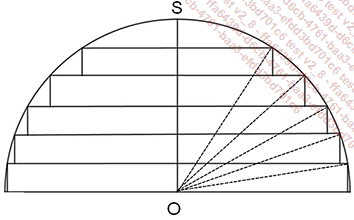
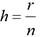 . Il y a n-1 cylindres dont les rayons ri sont
donnés, d’après le théorème
de Pythagore, par la formule
. Il y a n-1 cylindres dont les rayons ri sont
donnés, d’après le théorème
de Pythagore, par la formule 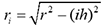 . Dans cette formule, l’indice i varie de 1 à n-1.
. Dans cette formule, l’indice i varie de 1 à n-1.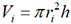 pour i variant
de 1 à n-1.
pour i variant
de 1 à n-1.2. Le second schéma montre comment on peut empiler des cylindres, 6 dans le cas de la figure, pour obtenir une valeur approchée par excès du volume de la même demi-boule.
Intégration approchée par la méthode des rectangles
Avec le calcul différentiel, le calcul intégral constitue l’autre branche du calcul infinitésimal. La mesure des grandeurs (longueur d’une courbe, aire, volume, travail, etc.) et le calcul des probabilités utilisent constamment des calculs d’intégrales. La méthode la plus simple pour calculer une intégrale est la méthode des rectangles.
1. Historique
L’origine de l’intégration se trouve dans les problèmes que se posaient les Grecs qui voulaient calculer des aires et des volumes. Au IVe siècle avant J.-C., Eudoxe a réussi à calculer le volume du cône et celui de la pyramide. Un siècle plus tard, Archimède a calculé le volume de la sphère ainsi que son aire. Il a réussi également à calculer l’aire du « segment » de parabole, délimité par cette courbe et une de ses cordes. Tous ces problèmes géométriques ont été repris et développés au cours des siècles, d’abord par les mathématiciens arabes puis par les mathématiciens européens. Le calcul intégral est créé au XVIIe siècle par les deux immenses mathématiciens que sont Leibniz (1646-1716) et Newton (1642-1727).
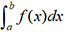 . Si on connaît une primitive d’une
fonction f intégrable
sur un intervalle...
. Si on connaît une primitive d’une
fonction f intégrable
sur un intervalle...Intégration approchée par la méthode des trapèzes
Cette méthode est analogue à la précédente à ceci près qu’on remplace les rectangles par des trapèzes. La vitesse du calcul et la précision des résultats en sont grandement améliorées.
1. Rappel
Considérons encore une fois une fonction numérique f définie et continûment dérivable sur un intervalle [a;b]. Choisissons un repère orthonormal et représentons graphiquement cette fonction sur cet intervalle. Soit S l’aire de la surface limitée par la courbe représentative de f, par l’axe des x et par les droites ∆1 et ∆2.
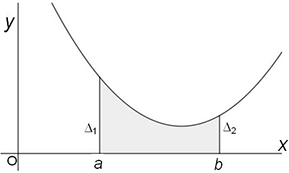
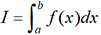 mesure la surface coloriée en gris
sur cette figure, on a I=S.
mesure la surface coloriée en gris
sur cette figure, on a I=S.2. Principe de la méthode des trapèzes
Comme le montre la figure suivante, on peut obtenir une valeur approchée de S en remplaçant la surface à mesurer par celle de n trapèzes de même hauteur. Un examen rapide de la figure permet de voir qu’on pourra espérer une meilleure précision qu’avec la méthode des rectangles.
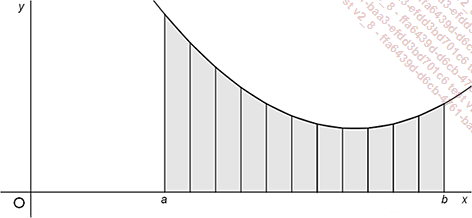
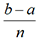 et pour bases respectives f(xi) et f(xi+1)
avec 1 ≤ i ≤ n. On a donc
et pour bases respectives f(xi) et f(xi+1)
avec 1 ≤ i ≤ n. On a donc 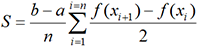 . Si f est
deux fois dérivable sur [a;b] et
s’il existe un nombre positif M tel
que
. Si f est
deux fois dérivable sur [a;b] et
s’il existe un nombre positif M tel
que 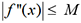 , on démontre que
, on démontre que 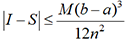 .
.3. Programme pour calculer l’intégrale d’une fonction continue
Dans le programme ci-dessous, nous avons encore défini f par la relation f(x)=3xex pour permettre la comparaison avec la méthode des rectangles. Comme précédemment, dans le cas d’une autre fonction, l’utilisateur du programme devra en donner la définition à la ligne 3 du programme.
# Intégration par la méthode...Intégration approchée par la méthode de Simpson
Quand on utilise la méthode des rectangles ou la méthode des trapèzes, on remplace des petits arcs de courbe par des segments de droite. La méthode de Simpson consiste à remplacer ces petits arcs de courbe par des arcs de parabole.
1. Historique
Le mathématicien anglais Thomas Simpson (1710-1761) s’est initié seul aux mathématiques supérieures de son époque en étudiant le calcul infinitésimal du marquis de l’Hospital (1661-1704) et les œuvres de Newton (1642-1727). Il a publié un traité de calcul infinitésimal intitulé Nouveau traité des fluxions et, dans le domaine de la statistique et du calcul des probabilités, un Traité sur la nature et les lois de la probabilité.
2. Méthode de Simpson13
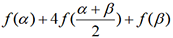 est une valeur approchée de l’intégrale
est une valeur approchée de l’intégrale 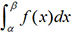 . Si xM et xM’ sont
les abscisses respectives des points M et M’ de la courbe qui représente
la fonction f, la méthode
consiste en fait à remplacer l’arc MM’ par un arc de parabole.
En appliquant la formule de Simpson à chacun des intervalles
qui résulte de la subdivision d’un intervalle [a;b] en
2n parties égales,
on obtient une valeur approchée de
. Si xM et xM’ sont
les abscisses respectives des points M et M’ de la courbe qui représente
la fonction f, la méthode
consiste en fait à remplacer l’arc MM’ par un arc de parabole.
En appliquant la formule de Simpson à chacun des intervalles
qui résulte de la subdivision d’un intervalle [a;b] en
2n parties égales,
on obtient une valeur approchée de 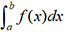 . Le programme qui utilise cette méthode
est le suivant :
. Le programme qui utilise cette méthode
est le suivant :# Intégration par la méthode de Simpson
from math import*
def f(x):
return (3**x)*exp(x)
a=eval(input("Valeur de a ?"))
b=eval(input("Valeur de b ?"))
n=eval(input("Valeur de l'entier n ?"))
long=(b-a)/2/n
s=0
for i in range(1,2*n,2): ...Intégration approchée par la méthode de Gauss
La méthode de quadrature de Gauss (1777-1855) permet de calculer de manière approchée l’intégrale d’une fonction continue sur un intervalle [a;b] mais est parfaitement exacte pour les polynômes de degré inférieur ou égal à 11.
1. Historique
Surnommé « le prince des mathématiciens », Gauss est considéré comme l’un des plus grands mathématiciens de tous les temps. Astronome et physicien aussi bien que mathématicien, il a dirigé l’observatoire de Göttingen mais ne travailla guère comme professeur de mathématiques, car il n’aimait pas enseigner !

Billet de banque allemand à l’effigie de Carl Friedrich Gauss
2. Principe de la méthode de Gauss
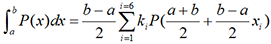 . Les valeurs des xi et des ki sont
les suivantes :
. Les valeurs des xi et des ki sont
les suivantes :|
x1=-0.932469514 |
k1=0.171324492 |
|
x2=-0.661209386 |
k2=0.360761573 |
|
x3=-0.238619186 |
k3=0.467913915 |
|
x4=-x3 |
k4=k3 |
|
x5=-x2 |
k5=k2 |
|
x6=-x1 |
k6=k1 |
3. Un programme de calcul
Le programme qui suit utilise la méthode de Gauss pour calculer l’intégrale sur un intervalle [a;b] d’une fonction f continue sur cet intervalle.
# Intégration par la méthode de Gauss
from math import*
def f(x):
return (3**x)*exp(x)
a=eval(input("Valeur de a ?"))
b=eval(input("Valeur de b ?"))
x1,x2,x3=-0.932469514,-0.661209386,-0.238619186
listedesx=[x1,x2,x3,-x3,-x2,-x1]
k1,k2,k3=0.171324492,0.360761573,0.467913915
listedesk=[k1,k2,k3,k3,k2,k1]
s=0
for j in range(0,6):
x=(a+b)/2+listedesx[j]*(b-a)/2 ... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

