Nombres complexes
Les nombres complexes dans Python
Les nombres complexes ont été inventés au XVIe siècle, en Italie. Malgré quelques différences, on peut faire avec eux à peu près les mêmes calculs qu’avec les nombres réels. C’est pourquoi Python possède un module particulier, le module « cmath », dédié à ces nombres.
1. Historique
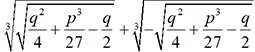 .
.
Autoportrait de Jérôme Cardan (1501-1576)
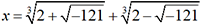 soit
soit 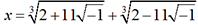 . Il appelle piu di meno le « nombre »
. Il appelle piu di meno le « nombre » 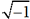 dont le carré vaut -1 et constate que
dont le carré vaut -1 et constate que 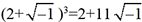 et
et 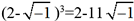 . Il en résulte
que
. Il en résulte
que 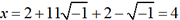 , ce qui est bien la solution
recherchée. Bombelli...
, ce qui est bien la solution
recherchée. Bombelli...Résolution dans C des équations du second degré
Le théorème fondamental de l’algèbre affirme que tout polynôme non constant à coefficients complexes admet au moins une racine. Dans le cas d’une équation du second degré, il y a toujours deux solutions dans C, que ses coefficients soient réels ou non.
1. Cas d’une équation à coefficients réels
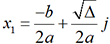 et
et 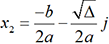 .
.Pour résoudre une telle équation, on peut utiliser le programme suivant (comme le fait Python, nous avons désigné par j au lieu de i le nombre complexe dont le carré vaut -1.) :
# Résolution dans C d'une équation du second degré
# à coefficients réels
from math import*
# Coefficients de l'équation
a=eval(input("Quelle est la valeur de a ? "))
b=eval(input("Quelle est la valeur de b ? "))
c=eval(input("Quelle est la valeur de c ? "))
# Calcul du discriminant
delta=b*b-4*a*c
print("delta=", delta)
# Résultat si delta>0
if delta>0:
x1=(-b+sqrt(delta))/2/a
x2=(-b-sqrt(delta))/2/a
print("1ère solution=", x1)
print("2ème solution=", x2)
# Résultat si delta=0
if delta==0:
x=-b/2/a
print("Une solution double x=",x)
# Résultat si delta...Les suites de nombres complexes
On étend aux suites à valeurs dans C toutes les propriétés des suites de nombres réels, sauf celles qui font référence à l’ordre puisque, contrairement à R, il n’existe pas de relation d’ordre sur C.
Comme chaque terme d’une suite (zn) est l’affixe d’un point Mn du plan complexe, les points Mn peuvent être représentés graphiquement grâce à leurs coordonnées.
1. Suites récurrentes
On peut utiliser Python pour calculer les n premières valeurs d’une suite récurrente (zn). Le terme général de cette suite peut être exprimé sous forme algébrique, sous forme trigonométrique ou bien sous forme exponentielle.
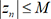 . Naturellement,
l’emploi de Python ne peut constituer une démonstration
des propriétés observées, mais il permet
de conjecturer certaines de ces propriétés.
. Naturellement,
l’emploi de Python ne peut constituer une démonstration
des propriétés observées, mais il permet
de conjecturer certaines de ces propriétés.2. Partie réelle et partie imaginaire d’une suite complexe
Soit (zn) une suite de nombres complexes. Chaque terme de cette suite peut s’écrire sous la forme algébrique zn=an+ibn. Les nombres réels an et bn sont donc les termes de deux suites. La suite (an) est la partie réelle de la suite (zn) tandis que la suite (bn) en est la partie imaginaire. Les suites (an) et (bn) sont souvent notées Re(zn) et Im(zn).
3. Convergence d’une suite
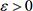 qui possède
la propriété...
qui possède
la propriété...Aperçu sur les fonctions d’une variable complexe
Soit z=x+iy un nombre complexe quelconque choisi dans C tout entier ou dans un sous-ensemble de C. On définit une fonction de C dans C en associant un nombre complexe z’=x’+iy’ à z. Comme les nombres z et z’ sont les affixes des points M(x;y) et M’(x’;y’), on définit du même coup une transformation plane φ du plan complexe dans lui-même en posant M’=φ(M).
1. Fonctions nouvellles
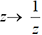 , z→
, z→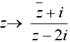 , etc. Si f est
une fonction telle que z’=f(z), le nombre z’ peut s’écrire z’=g(z)+ih(z), g(z) et h(z) étant des nombres réels.
On peut étudier algébriquement et analytiquement
les propriétés de la fonction f mais on ne peut pas la représenter
graphiquement14 puisqu’elle dépend
de deux variable réelles. On peut aussi étudier
les propriétés de la fonction associée φ qui envoie le point M(z) sur le point M’(z’). En choisissant f convenablement, on peut facilement
retrouver quelques transformations planes classiques15 comme
les translations, les rotations, les homothéties, les similitudes,
etc.
, etc. Si f est
une fonction telle que z’=f(z), le nombre z’ peut s’écrire z’=g(z)+ih(z), g(z) et h(z) étant des nombres réels.
On peut étudier algébriquement et analytiquement
les propriétés de la fonction f mais on ne peut pas la représenter
graphiquement14 puisqu’elle dépend
de deux variable réelles. On peut aussi étudier
les propriétés de la fonction associée φ qui envoie le point M(z) sur le point M’(z’). En choisissant f convenablement, on peut facilement
retrouver quelques transformations planes classiques15 comme
les translations, les rotations, les homothéties, les similitudes,
etc.2. La fonction z→ z+a
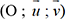 . Soit A(xA;yA) un point
quelconque du plan complexe et soit M, N et P trois autres points
dont les affixes respectifs sont m, n et p.
Le programme qui suit permet de choisir ces points et de calculer
les affixes m’, n’ et p’ de
leurs images M’, N’ et P’ par la fonction z→z+a.
. Soit A(xA;yA) un point
quelconque du plan complexe et soit M, N et P trois autres points
dont les affixes respectifs sont m, n et p.
Le programme qui suit permet de choisir ces points et de calculer
les affixes m’, n’ et p’ de
leurs images M’, N’ et P’ par la fonction z→z+a.# Fonction zz+a
from math import*
xA=eval(input("Valeur de xA ? "))
yA=eval(input("Valeur de yA ? "))
xM=eval(input("Valeur... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

