Les calculs statistiques
Introduction
Les calculs statistiques sont des techniques d’interprétation des données numériques. Ces calculs ont pour objet de permettre de tirer des conclusions à partir de données observées, conclusions qui échapperaient à un examen purement intuitif.
L’objectif est atteint en deux temps :
La collecte des données
C’est l’objet de la STATISTIQUE DESCRIPTIVE, qui consiste à fournir des indicateurs simples, peu nombreux et concis en vue de représenter une réalité physique ou économique.
L’interprétation des données
Cette phase permet de tirer des conclusions à partir de résultats observés sur un échantillon. C’est la STATISTIQUE INFÉRENTIELLE. On utilise à cet effet le CALCUL DES PROBABILITÉS pour définir quel est le modèle mathématique qui représente le mieux la réalité.
La statistique descriptive
La statistique descriptive travaille sur au moins une variable aléatoire dont les différentes valeurs sont observées sur un échantillon de données représentant un ensemble plus vaste appelé population. Les valeurs observées constituent une série statistique.
Exemple 1
La taille (variable aléatoire) des élèves de quelques classes terminales (échantillon) choisies parmi toutes les classes terminales de la région Bretagne (population) est mesurée.
Exemple 2
Le poids unitaire (variable aléatoire) de 100 paquets de biscuits (échantillon) prélevés sur la production quotidienne (population) d’une chaîne de fabrication est mesuré.
Les fonctions descriptives de base
Excel dispose de fonctions de statistiques descriptives qui sont toutes très similaires du point de vue de la syntaxe :
=NOMFONCTION(plage de cellules)
(sauf la fonction QUARTILE qui nécessite un deuxième argument indiquant la limite du quartile choisi)
Attention ! Dans la plage de cellules servant d’argument à la fonction statistique, seules les cellules contenant des nombres sont prises en compte dans le calcul. Les cellules vides et celles contenant du texte sont ignorées.
L’exemple qui va nous servir dans l’étude des différentes fonctions Excel concerne les temps d’attentes...
Le calcul des probabilités
La statistique descriptive permet de résumer une série de données par quelques indicateurs caractéristiques : la moyenne et l’écart-type par exemple. C’est insuffisant pour tirer parti de toute l’information contenue dans la série. Deux séries de données pourraient très bien avoir la même moyenne et le même écart-type et cependant être totalement différentes.
Le but du calcul des probabilités est de définir un modèle théorique, encore appelé "loi statistique" auquel peut être assimilée la répartition des données d’une série.
Si on appelle X la variable aléatoire représentant le temps d’attente aux urgences, la probabilité que X prenne une valeur donnée s’exprime par une fonction f(X) qui sera donc la "loi de probabilité" suivie par la variable X.
Rappelons que la probabilité d’une valeur va de 0 (impossibilité) à 1 (ou 100 %, certitude).
La loi Normale (ou Loi de Laplace-Gauss)
C’est la loi la plus répandue car beaucoup de cas pratiques correspondent à l’application de cette loi : données nombreuses, valeurs continues (temps, longueurs, poids, etc.), observations indépendantes. La fonction f(X) se présente sous la forme de la célèbre "courbe en cloche".
Pour étudier les exemples de fonctions Excel...
La statistique inférentielle
La statistique inférentielle est un ensemble de techniques qui, à partir des indicateurs de la statistique descriptive et des modèles du calcul des probabilités, va permettre de mesurer un risque, d’expliquer une variable par une ou plusieurs autres, de comparer des échantillons, de valider un modèle, etc. et finalement de prendre une décision.
Valider un modèle - Le test du χ2 de Pearson
Nous voulons tester l’hypothèse que les temps d’attente aux urgences suivent une loi normale. Pour cela, calculons ce que devraient être théoriquement les effectifs si leur répartition suivait la loi normale. Le tableau suivant montre les résultats et la manière dont ils ont été calculés grâce à la fonction LOI.NORMALE.N déjà étudiée.
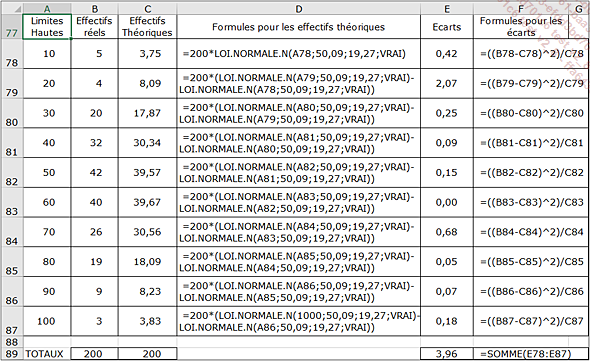
Le calcul du x2 est effectué en calculant les écarts pour chaque classe à l’aide de la formule (Eff. Réel-Eff. Théorique)²/Eff.Théorique. Les résultats se trouvent dans la plage de cellules E78:E87. Le x2 s’obtient en totalisant ces écarts : le résultat est 3,96 en cellule E89.
Comparons ce résultat avec le résultat de la fonction Excel LOI.KHIDEUX.INVERSE.DROITE. Cette fonction a pour argument une probabilité, c’est le risque de se tromper que nous acceptons de prendre (nous prendrons un seuil classique de 5 %) et un nombre de degrés de libertés égal à (nombre de classes-3), soit 7 dans notre cas.
Le résultat est le suivant :

Le x2 calculé (3,96) étant plus petit que le x2, nous pouvons conclure que le modèle de la loi normale peut être appliqué valablement à la variable X (temps d’attente), avec 5 % de risque d’erreur.
Expliquer une variable
Le principe consiste de façon générale à déterminer dans quelle mesure une variable Y est expliquée par une variable X (régression simple) ou par plusieurs variables X1, X2, ..., Xn (régression multiple) et, dans un deuxième temps, à valider la légitimité de leur liaison.
Le plus souvent, on se contente de régressions linéaires, autrement dit d’équations Y = a.X+b pour...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
