Les outils d'analyse de scénarios
Introduction
Excel propose une première technique, simple, en matière d’analyse de scénarios : la valeur cible. Il s’agit de partir d’un résultat donné et de chercher la valeur de la variable qui permet d’obtenir ce résultat. Dans bien des cas, cette technique est suffisante pour répondre aux problèmes courants de gestion simple.
Dans des cas plus complexes, Excel propose un complément important, le Solveur, qui permet le ciblage à partir de plusieurs variables ainsi que l’optimisation de fonctions économiques comme maximiser un gain ou minimiser un budget.
Les équations à une inconnue : la valeur cible
Pour ouvrir la boîte de dialogue de la valeur cible, cliquez sur l’onglet Données, puis sur le bouton Analyse scénarios - Valeur cible du groupe Prévision.

La boîte de dialogue Valeur cible apparaît :
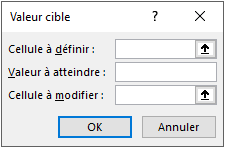
Les zones de saisie de cette boîte de dialogue sont les suivantes :
-
Cellule à définir : cellule, contenant obligatoirement une formule, dans laquelle la valeur cible doit être obtenue.
-
Valeur à atteindre : valeur souhaitée pour la cellule cible.
-
Cellule à modifier : cellule de saisie intervenant, directement ou en cascade, dans la formule de la cellule à définir.
Exemple 1
Un artisan présente à un client la facture finale des travaux qu’il vient de réaliser. Le montant facturé (5.269,33 €) dépassant le devis initial (5.000 €), le client demande à l’artisan que le montant facturé soit égal au montant du devis signé. Pour le satisfaire, l’artisan décide d’appliquer une remise au montant hors taxes de façon à obtenir le montant initial TTC de 5.000 € prévu au devis. Il cherche donc à connaître cette remise.

Onglet Données - groupe Prévision, cliquez sur le bouton Analyse de scénarios puis sur Valeur cible.
Complétez la boîte...
Les équations à plusieurs inconnues : le Solveur
Activer le Solveur
Le Solveur est un produit qui fait partie des Compléments Excel (ex "macros complémentaires"). Il n’est pas forcément présent dans la liste des onglets proposés par Excel par défaut. Il est donc nécessaire, au préalable, de l’activer. Procédez de la manière suivante :
Cliquez sur l’onglet Fichier, bouton Options.
Dans la boîte de dialogue qui s’affiche, cliquez dans le volet de gauche sur Compléments.
Sélectionnez l’option Compléments Excel de la liste déroulante en bas à gauche et cliquez sur le bouton Atteindre.
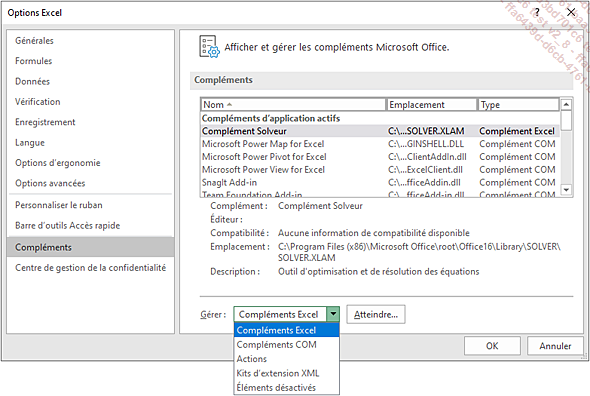
Une nouvelle boîte de dialogue apparaît :
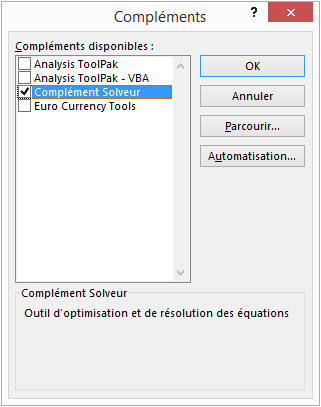
Cochez la case Complément Solver puis cliquez sur OK.
Le groupe Analyse, contenant le bouton Solveur, apparaît désormais à droite dans l’onglet Données.

La valeur cible à partir de plusieurs variables
La première application possible du Solveur Excel est le ciblage d’une valeur calculée à partir de plusieurs inconnues. C’est la généralisation de la technique vue à la section précédente.
Exemple 1
Un fournisseur a émis vers un de ses clients un grand nombre de factures à destination de divers services. Un paiement est effectué par le service Comptabilité Fournisseurs du client, sans que soient indiquées les factures qui sont ainsi réglées. Pour le suivi des règlements, il est impératif que le fournisseur sache quelles sont...
Optimiser à l’aide du Solveur
Le Solveur devient un outil encore plus performant dans les problèmes d’optimisation. Il permet de maximiser ou de minimiser une fonction économique en prenant en compte des contraintes techniques et éventuellement des contraintes mathématiques. Les exemples ci-dessous présentent la résolution de quelques problèmes classiques de programmes linéaires.
La minimisation d’un coût de production
Problème posé : le manager d’une station de radio souhaite minimiser le coût de production total d’une tranche horaire de 30 mn (11h à 11h30) tout en respectant la politique générale de la station qui lui impose une série de contraintes. La tranche horaire doit aborder les nouvelles locales, les nouvelles nationales, le sport et la météo. Combien de minutes de la tranche horaire doivent-elles être consacrées à chaque rubrique sachant que :
-
10 mn sont réservées à la publicité. Il reste donc 20 mn à répartir.
-
Au moins 15 % (3 mn) du temps disponible doit être affecté aux nouvelles locales.
-
La durée totale consacrée aux nouvelles doit être au moins égale à 50 % de la durée d’émission (10 mn).
-
Le temps consacré à la météo doit être inférieur ou égal au temps consacré au sport.
-
Le temps consacré au sport ne doit pas dépasser celui consacré aux nouvelles.
-
Au moins 20 % du temps doit être consacré à la météo.
-
Les coûts de production par minute sont de 300 € pour les nouvelles locales, 200 € pour les nouvelles nationales, 100 € pour la météo et le sport.
Formalisation : nommons L, N, S et M les variables représentant les durées affectées respectivement aux nouvelles locales, nationales, au sport et à la météo. La fonction économique est le coût de production total :
Coût = 300.L + 200.N + 100.S + 100.M
Et les contraintes fonctionnelles :
-
L + N + S + M = 20
-
L >= 3
-
L + N >= 10
-
M <= S
-
S <= (L + N)
-
M >= 4
Rajoutons également la contrainte mathématique : L, M, S, N >=0, une durée ne pouvant pas être négative....
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
