Les nombres complexes
Rappels sur les nombres complexes
La forme classique d’un nombre complexe est :
Z = a + i.b
a est la partie réelle et b la partie imaginaire avec i2 = -1. À noter que les électriciens adoptent la forme Z = a + j.b, "i" étant traditionnellement réservé à l’intensité du courant.
Les autres formes possibles sont :
-
la forme trigonométrique : Z =ρ(Cosθ+ i.Sinθ)
-
la forme exponentielle : Z =ρeiθ
ρ est le module, θ l’argument. Les relations avec la forme classique sont les suivantes :
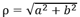
La figure suivante donne une représentation géométrique des nombres complexes.
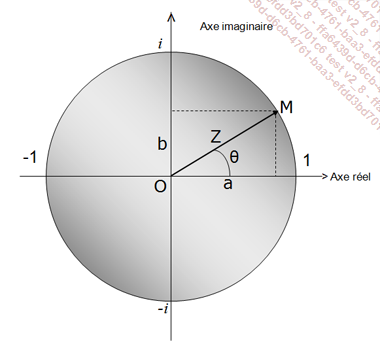
Le conjugué de Z est Z’ = a - i.b. Les opérations que l’on peut effectuer sur les nombres complexes sont similaires à celles effectuées sur les nombres réels : somme, différence, produit, division, puissance, exponentielle, etc.
Les fonctions Excel de nombres complexes
Avec Excel 2019, les nombres complexes font partie intégrante des contenus des cellules. Au niveau de la saisie, il suffit de taper un contenu textuel de la forme a+ib (ou a+jb) dans une cellule pour que ce contenu soit reconnu ultérieurement comme un nombre complexe valide. De même, pour utiliser un nombre complexe fixe comme argument d’une fonction, il suffit de le noter entre guillemets, comme pour n’importe quel texte.
Si la partie réelle (a) est négative, il faut commencer la saisie directe du nombre complexe par une apostrophe (’).
Attention ! Il n’est pas possible de mélanger les notations "i" et "j" dans une même opération.
La fonction COMPLEXE permet de construire un nombre complexe à partir de ses parties réelle et imaginaire. La syntaxe est la suivante :
=COMPLEXE(partie réelle;partie imaginaire;notation)
L’argument notation est égal à "i" ou "j". S’il est ignoré c’est la notation courante "i" qui est choisie.
L’extrait de feuille Excel ci-dessous fournit quelques exemples de notation des nombres complexes :
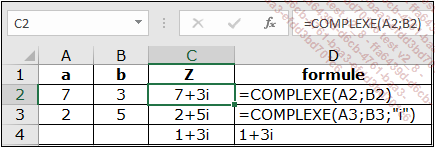
Et voici un autre exemple sur la notation trigonométrique (l’angle choisi en B8 est π/6 soit 30 degrés) :
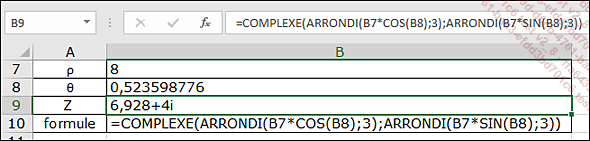
Dans le tableau suivant, les différentes fonctions d’Excel 2019 s’appliquant...
Les nombres complexes en géométrie
Les nombres complexes s’appliquent à de nombreux problèmes de géométrie plane en associant à un vecteur OM de coordonnées (a, b) le nombre complexe Z = a + i.b, qui est l’affixe du vecteur OM (ou du point M), le point O étant l’origine des axes d’un repère orthogonal.
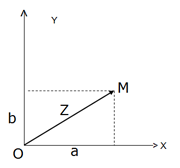
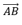
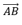 s’écrit
: ZAB = ZB-ZA.
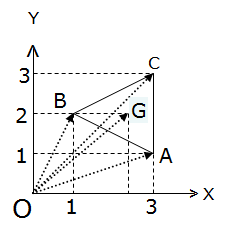
Dans le cas de figure ci-dessous, le vecteur
s’écrit
: ZAB = ZB-ZA.
Dans le cas de figure ci-dessous, le vecteur 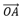 a pour affixe ZA = 3+iet
le vecteur
a pour affixe ZA = 3+iet
le vecteur  , ZB = 1+2i.
, ZB = 1+2i.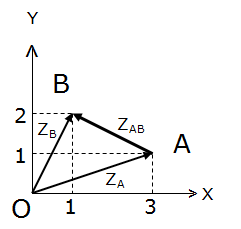
Le calcul ZAB = ZB - ZA est réalisé à l’aide de la fonction COMPLEXE.DIFFERENCE qui donne le résultat : ZAB= -2 + i.
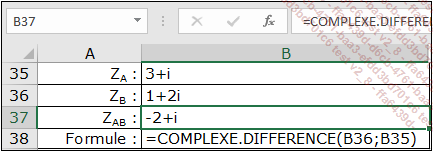
Affixe du barycentre
L’exemple choisi est celui du centre de gravité d’un triangle ABC.
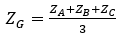 .
.Pour l’exemple, gardons les valeurs précédentes de ZA et ZB et prenons ZC= 3 + 3i.
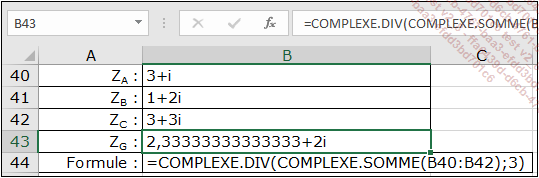
Dans la formule de calcul Excel, la fonction COMPLEXE.SOMME est utilisée pour additionner les 3 affixes, puis la fonction COMPLEXE.DIV pour diviser le résultat par 3.
Homothétie
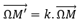 .
.En termes d’affixes de nombres complexes...
Les nombres complexes en électricité
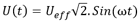 et l’intensité correspondante par :
et l’intensité correspondante par :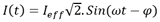
-
U(t) : valeur instantanée de la tension
-
Ueff : valeur efficace de la tension
-
ω : pulsation. ω=2πf où f est la fréquence, généralement 50 Hz.
-
I(t) : valeur instantanée de l’intensité
-
Ieff : valeur efficace de l’intensité
-
φ : déphasage de I par rapport à U
Expression de la loi d’Ohm en nombres complexes
Cette loi s’exprime par la formule : U=Z.I ou I=U / Z
Z est l’impédance complexe du composant ou du circuit. Elle est mesurée en ohms (Ω). On utilise également les notions suivantes :
-
L’admittance : Y = 1/Z, mesurée en Siemens (Y=G + jB)
-
La conductance : G, partie réelle de l’admittance
-
La susceptance : B, partie imaginaire de l’admittance
À partir de ces formules, on obtient aussi les valeurs : I=Ueff/|Z| (|Z| est le module de Z) et φ = Argument(Z) si on prend comme convention de placer la tension complexe U sur l’axe des nombres réels.
Pour les impédances en série, l’impédance résultante est : Z = Z1 + Z2 + Z3+ ...
Et en parallèle : 1/Z = 1/Z1 + 1/Z2 + 1/Z3 + ...
Le tableau suivant résume les impédances des composants élémentaires...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
