Analyse des données
Introduction à l’analyse des données

Nuage de mots des termes techniques et informatiques utilisés pour ce chapitre
1. Définition et rôle de l’analyse de données
Dans le cadre de l’analyse exploratoire de données (couramment appelée EDA pour Exploratory Data Analysis), exploration et analyse fonctionnent en tandem pour approfondir notre compréhension des informations, visibles ou cachées, que révèlent les données. Tandis que l’exploration nous a permis de porter un premier regard et d’identifier des schémas initiaux, l’analyse nous permet de parfaire cette connaissance par un examen plus minutieux, grâce notamment à des outils statistiques qui permettent de mesurer les phénomènes observés et de valider s’ils peuvent être considérés comme significatifs ou non.
Prenons l’exemple d’un puzzle : là où l’exploration nous permettrait d’entrevoir, à travers l’examen des formes et des couleurs, la possibilité d’assembler certaines pièces, l’analyse représenterait l’examen minutieux qui confirmerait la faisabilité des différents assemblages.

2. Enjeux
Les tests statistiques et les méthodes d’analyses exploratoires sont essentiels dans l’étude des données. Grâce aux connaissances nouvelles qu’ils apportent, nous allons avoir l’opportunité d’innover, de prendre conscience des contraintes et d’améliorer la prise de décision.
a. Innovation et créativité
L’apport de nouvelles informations, illustrées de trois façons différentes et décrites ci-dessous, favorisera l’émergence de l’innovation et de la créativité. Cette compréhension approfondie des données nous permettra ainsi de concevoir des solutions originales.
Identification des caractéristiques importantes
En premier lieu, l’analyse nous permet d’identifier les éléments ayant un impact significatif sur le domaine étudié. Nous pourrons ainsi déterminer les variables...
Statistiques descriptives et inférentielles
L’analyse des variables nécessite de revoir certaines notions de statistiques. Il n’est nullement question ici de se noyer dans les détails mais simplement de comprendre les principaux outils nécessaires à l’analyse.
L’analyse statistique repose sur deux piliers que sont les statistiques descriptives et les statistiques inférentielles, chacune jouant un rôle bien spécifique.
Les statistiques descriptives ont pour objectif de décrire et résumer au mieux un ensemble de données. Pour faciliter la compréhension et l’application des concepts, nous allons étudier séparément les mesures pour les variables quantitatives et les variables catégorielles. Cette approche permettra de bien distinguer les méthodes spécifiques à chaque type de variable.
Les statistiques inférentielles permettent de généraliser les caractéristiques d’un échantillon de données à une population générale, dans le but de faire des prédictions. Nous utiliserons des tests spécifiques à chaque typologie de cas qui valideront ou non nos hypothèses.
Avant de faire connaissance avec les différentes statistiques, il est utile de définir la notion de robustesse, qui va être largement abordée. Un test ou une mesure est dit robuste s’il fournit des résultats fiables et précis même lorsque les conditions idéales ne sont pas toutes réunies. Voici les situations qu’un test ou une mesure robuste doivent pouvoir gérer :
-
la présence de valeurs aberrantes ;
-
la non-normalité de la distribution ;
-
les données ordinales ;
-
les ex aequo.
Cette robustesse est essentielle pour garantir des conclusions valides dans des conditions variées.
1. Description des variables quantitatives
L’examen des variables quantitatives, également appelées continues, s’opère en trois étapes : identifier le centre, décrire la variabilité autour de ce centre, et analyser plus généralement la distribution des valeurs de la variable.
a. Mesures de tendance centrale
La mesure de la tendance centrale repose principalement sur trois outils :...
Modules Python pour l’analyse de données
Avant de choisir et de mettre en œuvre les différents tests statistiques, il est opportun de faire un point sur les possibilités offertes par les bibliothèques Python en la matière.
1. Les capacités limitées des modules classiques
Les librairies classiques telles que Pandas ou Numpy proposent, en plus de leurs fonctions pour manipuler les données, quelques fonctions pour calculer des indicateurs statistiques. Ces capacités se bornent aux statistiques descriptives ainsi qu’à la possibilité de calculer la corrélation et la covariance. Bien que certaines aient déjà été abordées précédemment, voici un tableau synthétique permettant de récapituler leurs possibilités :
|
Fonction |
Pandas |
NumPy |
|
Moyenne |
|
|
|
Médiane |
|
|
|
Mode |
|
Non disponible |
|
Écart-type |
|
|
|
Variance |
|
|
|
Minimum |
|
|
|
Maximum |
|
|
|
Résumé Statistique |
|
Non disponible |
|
Percentiles |
|
|
Tests statistiques de normalité
1. Contexte et objectif
Les tests de normalité de distribution constituent une étape fondamentale dans l’analyse des données, en particulier pour les variables numériques. Ils ont pour objectif de déterminer si la distribution d’une variable suit une loi normale. Cette vérification est essentielle, car elle influence le choix des méthodes statistiques à appliquer par la suite, afin de déterminer s’il existe un lien entre les variables. En effet, la normalité d’une variable conditionne le recours à des tests paramétriques, qui supposent une distribution normale des données, ou à des tests non paramétriques, mieux adaptés lorsque cette condition n’est pas remplie.
Avant de passer au test à proprement parler, il est intéressant de présenter les Quantile-Quantile plots (Q-Q Plots) qui offrent une manière intuitive et visuelle de représenter la normalité des données.
2. Les Q-Q plots
a. Définition et tracé du graphique
Les Q-Q plots (QQ pour Quantile-Quantile) sont des graphiques qui comparent les quantiles d’un jeu de données avec les quantiles d’une distribution théorique, souvent la distribution normale. En traçant les quantiles observés et les quantiles théoriques, nous pouvons aisément voir si nos données semblent normalement distribuées ou non.
Prenons un exemple que nous allons commenter pour comprendre comment utiliser ce type de visualisation :
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as stats
# Import du jeu de données des iris
iris = sns.load_dataset(“iris”)
# Sélection d'une colonne numérique
data = iris[‘sepal_length']
# Création d'un Q-Q plot
plt.figure(figsize=(5, 3))
stats.probplot(data, dist= »norm », plot=plt)
# Modification de la couleur des points
dots = plt.gca().get_lines()[0]
dots.set_markerfacecolor(‘#439cc8')...Tests statistiques bivariés
Les tests statistiques bivariés examinent la relation entre deux variables pour identifier des associations ou des différences significatives, aidant ainsi à comprendre les liens potentiels et à formuler des hypothèses de recherche pour faciliter la prise de décision. Ils fournissent également une base pour des analyses plus complexes, telles que la régression et les modèles multivariés.
Nous allons suivre le schéma suivant pour les étudier en commençant par les tests portant sur deux variables de même nature puis ceux sur deux variables de nature différente.
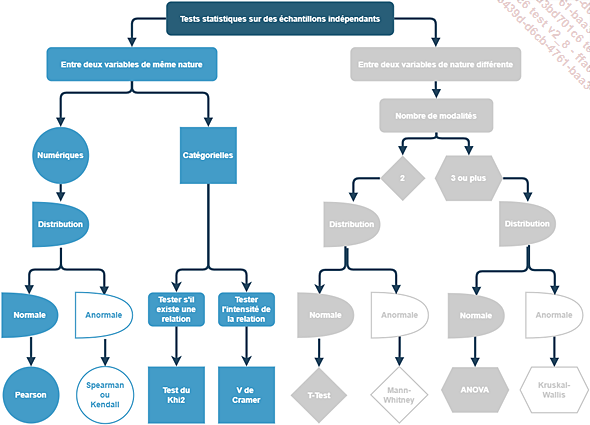
Nous nous concentrerons sur les tests portant sur des échantillons indépendants, c’est-à-dire des groupes qui sont totalement distincts les uns des autres. Il faut signaler qu’il existe également des tests sur les groupes appariés qui portent sur un même groupe où chaque observation est associée à une observation correspondante dans un autre groupe. C’est le cas, par exemple, pour un groupe avant et après un traitement médical. Afin de ne pas nous noyer sous les informations, ce cas de figure sera laissé de côté mais une simple recherche permettra de facilement trouver le test adéquat.
1. Tests bivariés entre des variables de même nature
a. Corrélations entre variables numériques
Principe et enjeux de la corrélation
Débutons cette familiarisation avec les tests bivariés par les corrélations de type linéaire, c’est-à-dire lorsque la relation entre deux variables peut être décrite par une ligne droite.
Ces tests entre deux variables numériques sont primordiaux, car ils nous permettent de mesurer entre -1 et 1, la force du lien existant entre les deux variables. Une corrélation de 1 indique une relation parfaitement positive, -1 une relation parfaitement négative, et 0 aucune relation. Les corrélations sont donc essentielles pour identifier et quantifier les relations linéaires potentielles entre des variables, et sont souvent visualisées à l’aide de matrices de corrélation ou de nuages de points.
Voici un schéma illustratif montrant le coefficient de corrélation...
Analyse multivariée
L’analyse multivariée a pour objectif d’examiner simultanément plusieurs variables pour comprendre les relations complexes et les interactions qui existent entre elles. Elle permet de révéler des patterns cachés et de fournir une vue d’ensemble cohérente sur le fonctionnement global d’un jeu de données. C’est une étape essentielle qui finalise l’analyse des données et permet d’identifier avec certitude les variables les plus importantes et les lois qui régissent le jeu de données étudié.
Avant d’aborder l’Analyse en Composantes Principales (ACP), qui constitue un pilier fondamental de l’analyse multivariée, nous explorerons deux autres techniques qui répondent à des besoins spécifiques : l’analyse de la variance multivariée (MANOVA) et l’Analyse des Correspondances Multiples (ACM).
1. Analyse de la variance multivariée (MANOVA)
a. Présentation et champs d’applications
La MANOVA est une généralisation de l’ANOVA qui vise à déterminer si une ou des variables catégorielles ont des liens avec les moyennes de plusieurs variables numériques dépendantes. Elle est particulièrement utile pour évaluer les effets combinés de plusieurs facteurs et mieux comprendre les relations complexes entre plusieurs variables.
b. Cas pratique d’utilisation
Prenons le jeu de données des diamants fourni par Seaborn :
import seaborn as sns
df = sns.load_dataset("diamonds")
df.head() 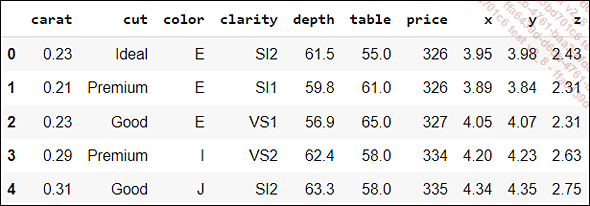
Il serait intéressant de savoir si les variables qualitatives décrivant la coupe et la couleur (cut et color) ont un impact sur des variables numériques comme les carats et le prix (carat et price). C’est l’occasion de mettre en œuvre une MANOVA en utilisant le module statsmodels :
from statsmodels.multivariate.manova import MANOVA
# Formule pour MANOVA
formula = 'carat + price ~ cut + color'
# Ajustement du modèle MANOVA
manova = MANOVA.from_formula(formula, data=df)
result = manova.mv_test()
# Affichage des résultats
print(result) 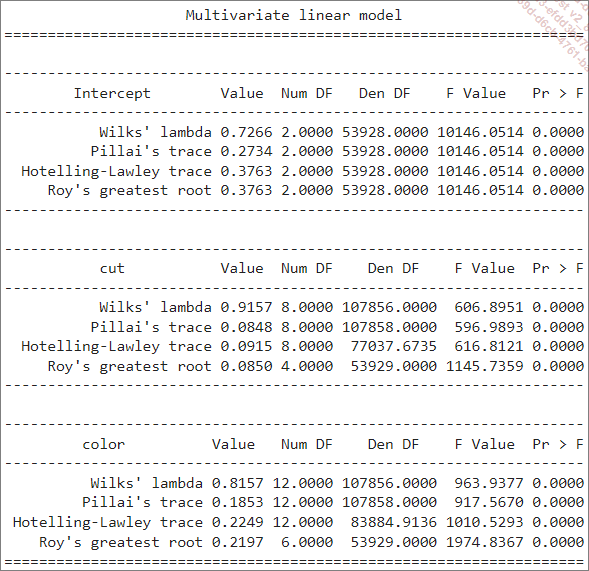
L’algorithme MANOVA utilise différents tests pour valider...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations


