Introduction

L’apprentissage supervisé vise à prédire une valeur ou l’appartenance à une catégorie en s’appuyant sur un large choix d’algorithmes dédiés. L’objet de ce chapitre est de faire connaissance avec ces différentes familles d’algorithmes et de les mettre, ensuite, en pratique dans un exemple complet de régression puis de classification.

Les familles d’algorithmes

Nous avons vu précédemment que les algorithmes de Scikit-Learn sont bien identifiés en fonction de leur finalité : les algorithmes dédiés à la régression ont tous un nom qui se termine par Regressor et ceux dédiés à la classification ont tous un nom se finissant par Classifier.

Nous allons ici dépasser cette notion de destination pour nous intéresser à l’esprit de chaque algorithme, indépendamment de sa finalité. Ce sera ainsi l’occasion de mieux connaître les caractéristiques de chacun et de les employer à meilleur escient.

Notre approche sera ainsi découpée en trois grandes familles : les algorithmes linéaires, semi-linéaires et non linéaires. Nous y aborderons chaque grande famille d’algorithmes, comment les installer et les paramètres externes à ajuster pour optimiser leurs performances. Ces paramètres externes sont qualifiés d’hyperparamètres.

1. Les algorithmes linéaires

Les algorithmes linéaires cherchent basiquement à établir une relation linéaire entre des caractéristiques et une variable cible. Ce type de lien, plutôt simple, les destine à expliquer des systèmes peu complexes. Ce sont donc des options à privilégier dès le début qui refléteront, suivant les résultats, la complexité du système et serviront de référence pour comparer les performances d’algorithmes gérant des relations plus complexes. Découvrons sans tarder les membres de cette famille.

a. Les régressions

La régression linéaire et la régression logistique sont des techniques linéaires où l’effet des variables indépendantes sur la variable cible est supposé être additif et proportionnel. Ce sont les seuls algorithmes de Scikit-learn dont le nom ne se termine pas par Regressor ou Classifier bien qu’elles représentent respectivement chacun d’entre eux. Avant de passer à l’étude particulière de chacune d’elle, notons qu’il peut y avoir une ou plusieurs variables explicatives. Dans le cas d’une seule, nous parlons de régression...

La régression en pratique

C’est le jeu de données des diamants qui sera utilisé ici pour expérimenter les étapes d’une modélisation de régression. Ce jeu possède 53 940 observations sur différentes caractéristiques des diamants comme les carats, la taille, la couleur, les dimensions ou le prix. Nous souhaiterions prédire le prix d’un diamant à partir de la table (largeur du sommet du diamant par rapport au point le plus large), du nombre de carats et de sa couleur.

Un travail préalable de feature engineering a été effectué, ce qui explique pourquoi certaines variables seront directement sélectionnées ou ignorées dans notre exemple. Le but étant de se concentrer ici uniquement sur la modélisation.

1. Préparation des données

a. Import des données

Nous commençons par importer les données en prenant soin de supprimer les observations ayant des dimensions nulles ou extrêmement élevées. Cette suppression ne concerne que 23 observations.

import seaborn as sns 
 
df_brut = sns.load_dataset("diamonds") 
 
# Conservation des mesures valides et non aberrantes 
condition = 'x != 0 and 0 < y < 30 and 0 < z < 30' 
df = df_brut.query(condition).reset_index(drop=True) 
 
df.head()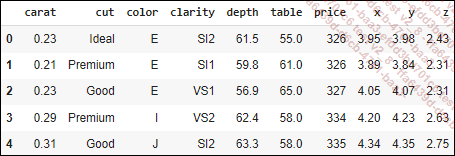

Avant d’aller plus loin, regardons la distribution de la variable price :

# Boxplot de price 
sns.boxplot(x=df['price'],color="#439CC8",width=0.5) 
plt.title("Boîte à moustaches des prix des diamants\n") 
plt.show()

Les prix des diamants s’échelonnent de 326 à 18 823 euros avec un prix médian à 2401 et un prix moyen d’environ 3931 euros.

b. Séparation des variables explicatives de la variable cible

La première mesure après l’importation va consister à séparer les variables explicatives de la variable à expliquer en les plaçant dans deux tables différentes X et y.

X = df[["table","carat","color"]] # Variables explicatives 
y = df["price"]                   #...

La classification en pratique

Nous allons maintenant pratiquer une classification. Pour cela, nous reprendrons l’exemple des « diamonds » en essayant maintenant de déduire la qualité de la taille du diamant à partir d’autres variables.

1. Préparation des données

a. Import des données

Commençons par importer les données et supprimer directement les mesures inexistantes ou aberrantes :

import seaborn as sns 
import pandas as pd 
import numpy as np 
 
# Import du jeu de données 
df = sns.load_dataset("diamonds") 
 
# Suppression des mesures inexistantes ou aberrantes 
df = df_brut.query('x != 0 and 0 < y < 30 and 0 < z < 30') 
.reset_index(drop=True)

b. Séparation entre les variables explicatives et la variable cible

Nous allons ensuite préparer les matrices X et y. Attention ici de bien passer la matrice y en type category :

# Préparation des matrices X et y 
X = df[["price","table","depth","color","clarity"]] 
y = pd.Series(df['cut'], dtype='category')

c. Séparation entre données d’entraînement et de test

La séparation entre les données d’entraînement et de test s’effectue ensuite de la manière suivante :

from sklearn.model_selection import train_test_split 
 
# Division des données entre train et test 
X_train, X_test, y_train, y_test = train_test_split(X, y, 
test_size=0.2, random_state=42, stratify=y)

L’usage de stratify dans la fonction train_test_split permet de maintenir les proportions des classes entre les ensembles d’entraînement et de test

d. Transformation des colonnes

Une fois les données séparées, nous allons les transformer de manière spécifique en fonction de leur type à l’aide de la fonction ColumnTransformer. Après avoir désigné les variables numériques et catégorielles, nous appliquerons respectivement une standardisation pour les unes et une binarisation pour les autres :

from sklearn.compose import ColumnTransformer 
 
# Identification des colonnes numériques et binaires 
numeric_columns = X.select_dtypes(include=['number']).columns ...

Conclusion

En conclusion, ce chapitre a introduit les principes fondamentaux de la modélisation supervisée en régression et en classification. Nous avons couvert les concepts essentiels tout en omettant certaines notions pour éviter une surcharge d’information. Il est important de souligner, à ce propos, que la gamme d’outils et de techniques disponibles est à la fois abondante et parfois complexe.

Pour véritablement maîtriser ces méthodes, une pratique régulière est indispensable. En approfondissant notre compréhension et en appliquant ces techniques dans divers domaines, nous pourrons affiner nos analyses, élargir notre boîte à outils, et développer des compétences plus avancées.

Le tableau ci-joint est un résumé des expérimentations abordées :

Aspect	Régression	Classification
Variable cible	Variable continue (quantitative)	Variable discrète (catégorielle)
Évaluation des performances	Erreur quadratique moyenne (MSE), Erreur absolue moyenne (MAE), R²	Matrice de confusion, Accuracy, Précision, Rappel, F-score
Hypothèses du modèle	Relation linéaire ou non, indépendance des observations et des variables
Prétraitement des données	Normalisation/Standardisation des variables Détection des valeurs aberrantes Encodage des variables...